CS229
1.Lecture 1
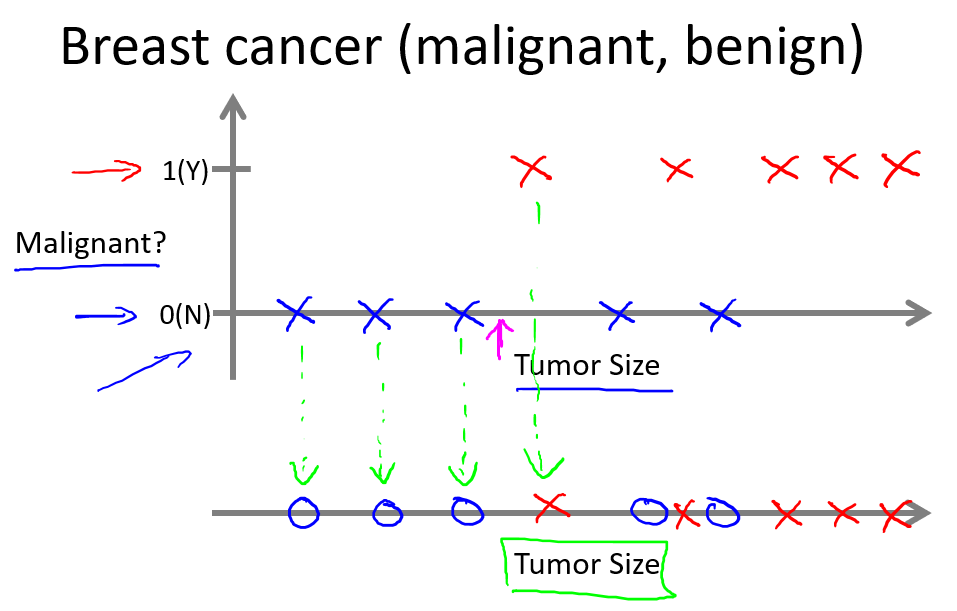
가장 널리 인용되는 머신러닝의 정의:Arthur Samuel (1959): Field of study that gives computers the ability to learn without being explicitly programmed정답이 있는 데이터셋을 학습한
2.Lecture 2
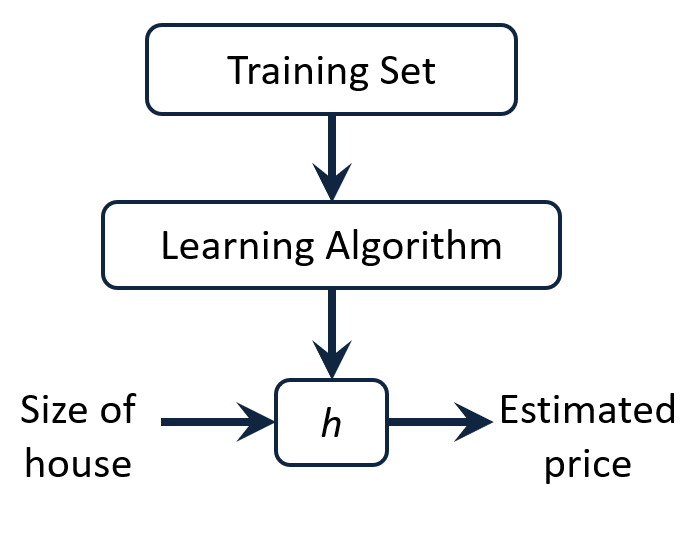
Process of supervised learning: feed training set to a learning algorithm, and make prediction about housing pricesUntitledsize of house 라는 입력값이 $h$함수
3.Lecture 3
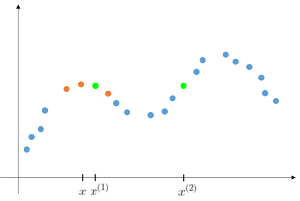
확률적 해석을 하는 이유!“cost function J가 왜 최소 제곱의 합의 꼴인가에 대한 유도를 하기 위해 “확률 분포란: 수집 및 관측된 데이터의 발생 확률을 잘 근사하는 분포보통 $p(x|\\theta)$로 표현한다. $\\theta$ 추정의 목적: 데이터의 실
4.Lecture 4
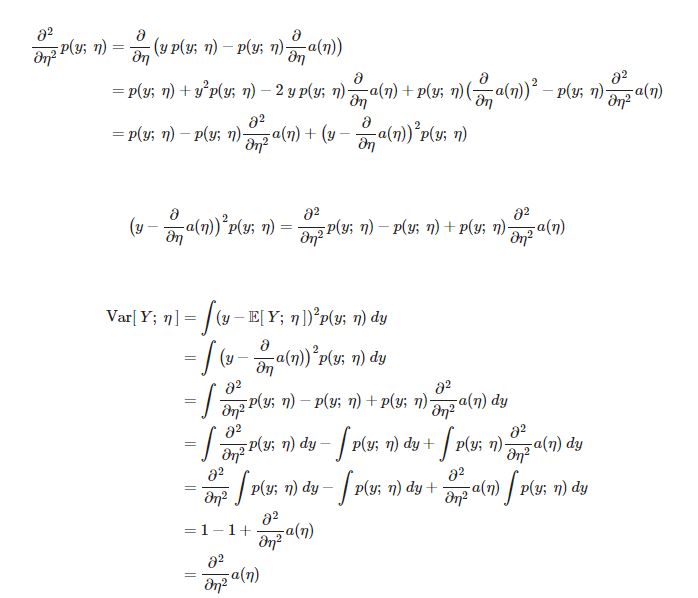
지금까지 regression 예제 $y\\mid x;\\theta ~ N(\\mu,\\sigma^2)$와 classification 예제 $y\\mid x;\\theta ~ Bernoulli(\\phi)$ 를 살펴보았다. 이번 강의 에서는 두가지 방법이 모두 GLM
5.Lecture 5
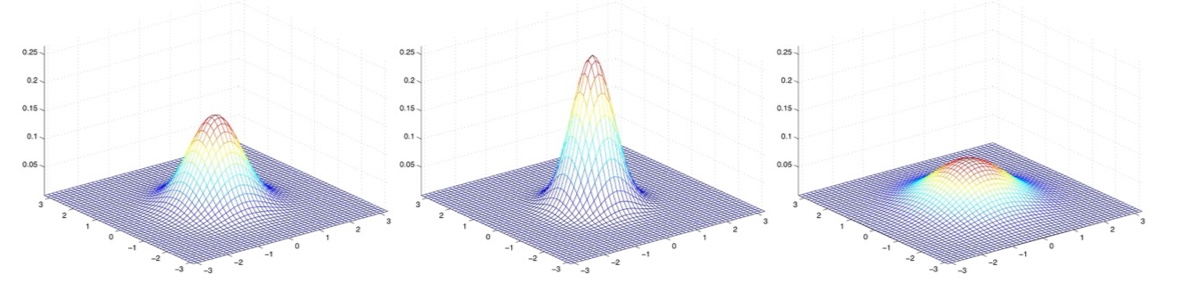
Generative learning algorithm : Learn $p(x|y)$ ( x is a features. y is a class. $p(y)$ is called class prior. )Generative learning algorithm 은 p(x|y
6.Lecture 6
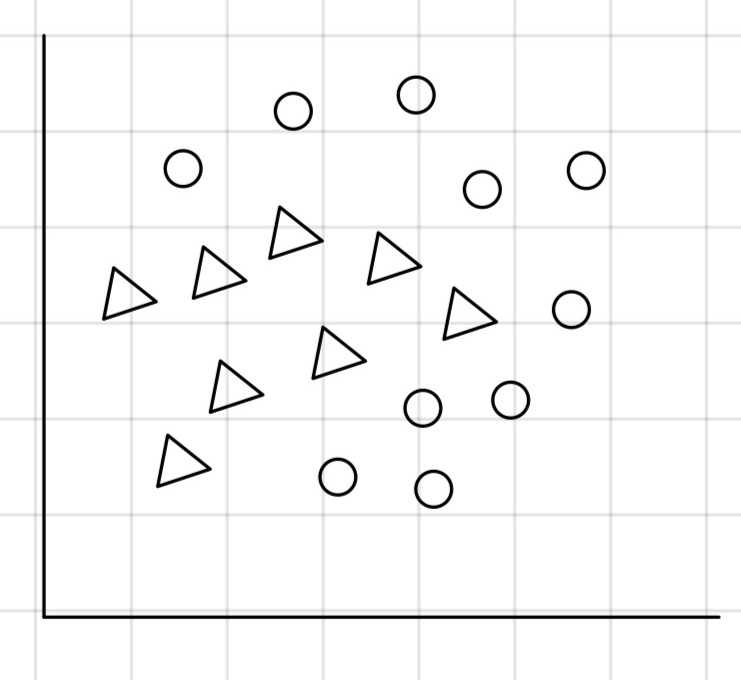
Naive Bayes에서 feature x가 다음과 같은 베르누이 분포가 아닌 $x\\in{1,....,k}$ 인 Multinomial value를 가질 때, 쉽고 빠르게 일반화가 가능하다. 또한, 입력값이 연속적인 경우에도 이를 부분으로 나누어 이산화 시켜 적용이
7.Lecture 7
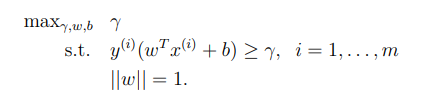
SVM의 목적은 margin을 최대화 하는 것이기 때문에 다음과 같이 식을 쓸 수 있다.optimization problem $\\mid\\mid\\omega\\mid\\mid = 1$ 는 functional margin 과 geometric margin이 똑같게 해
8.Lecture 8
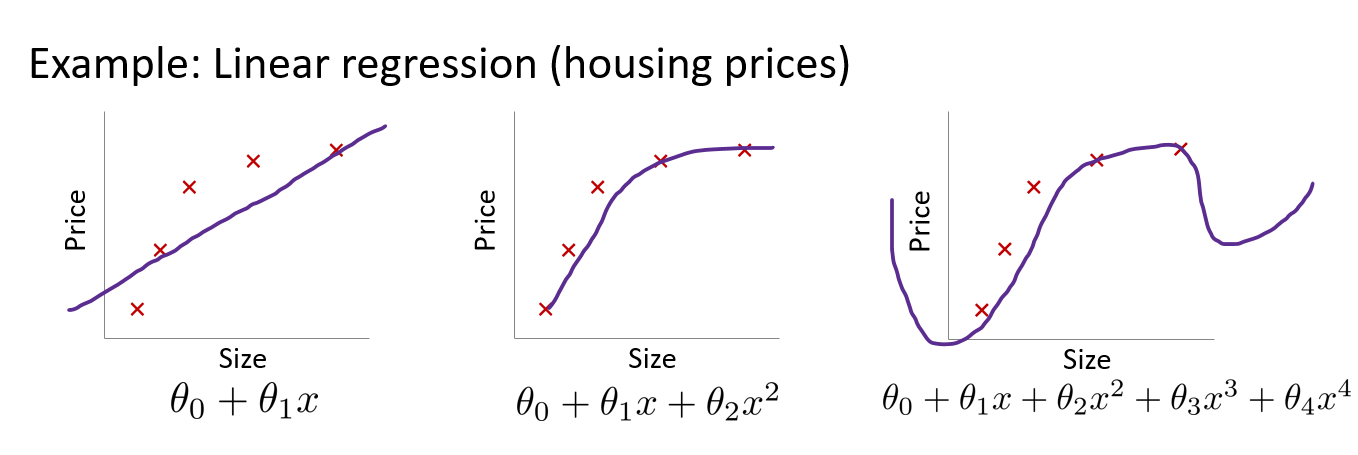
데이터셋에 어떤한 Bias가 있는지, 어떠한 variance가 있는지 알아보고 학습 알고리즘을 개선한다.Underfitting, high bias집의 가격과 집의 크기 사이의 관계가 선형적이라는 강한 편견)예측값과 실제 정답과의 차이가 크다.Just fitOverfit
9.Lecture 9
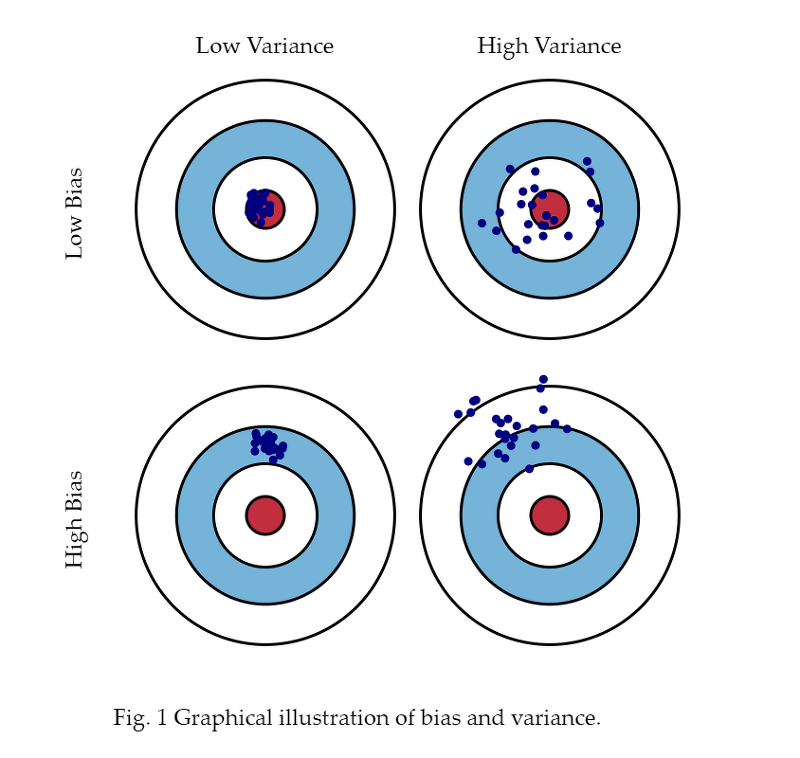
강의를 시작하기에 앞서 가정을 하고 시작을 하고자 한다.데이터(x,y)는 분포를 가지고 (Data Distribution) 이 때, Train data 와 Test data 둘다 동일한 분포를 가진다.모든 데이터 샘플들이 Independent samples이다. 또한
10.Lecture 10
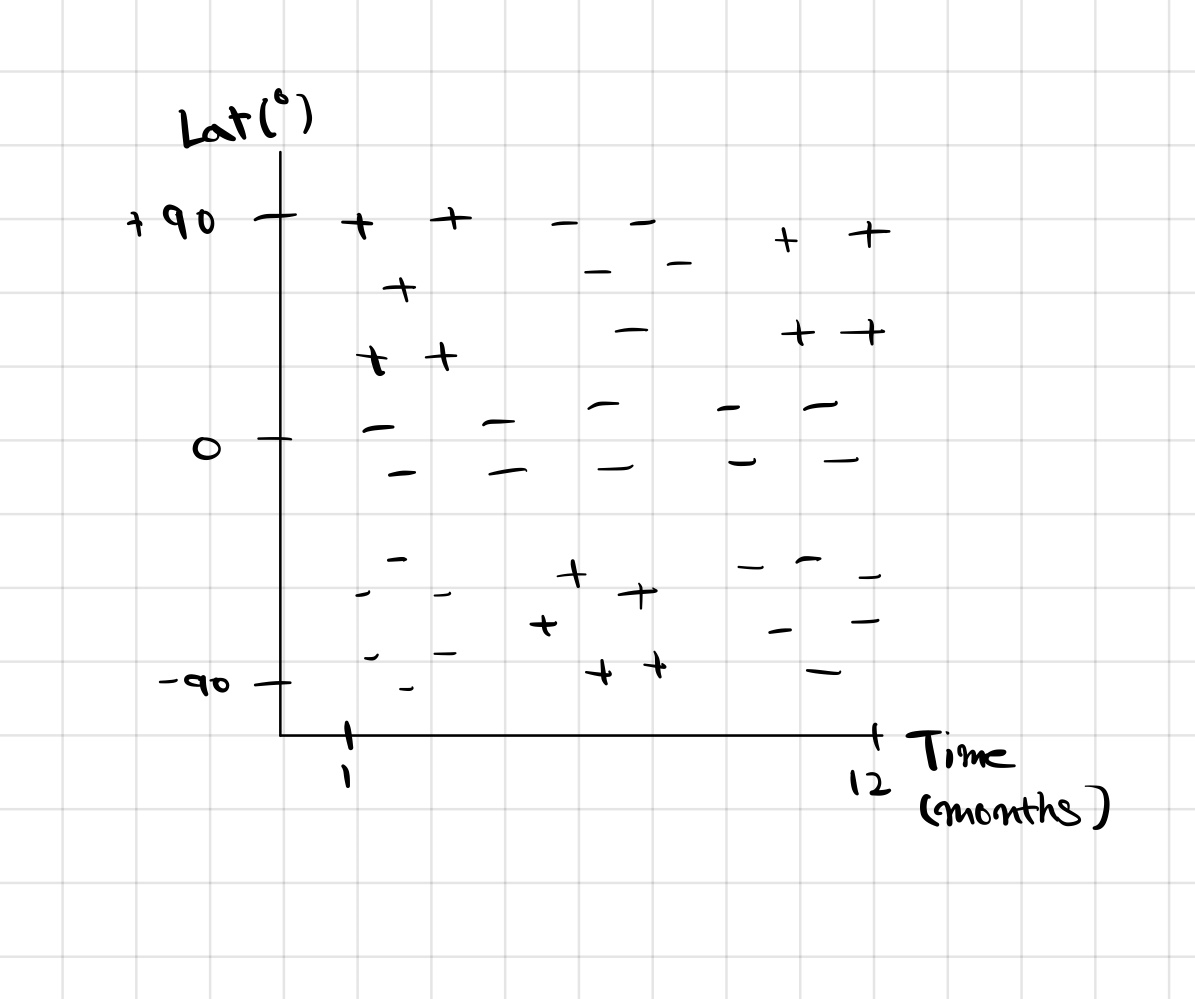
우선, 시간과 위도에 따른 스키를 탈 수 있는지 없는지를 알려주는 classifier를 만들어 보면 다음과 같다. 이것을 +와 -로 구분하기 위해서 아마도 SVM이나 Kernel을 생각할 수 있다. 하지만 Decision Tree를 사용하면 자연스럽게 가능하다. Des
11.Lecture 11
딥러닝에 대한 간략한 소개딥러닝은 머신러닝의 하위분류 중 하나로써 특히 컴퓨터 비전, 자연어 처리, 음성인식 업계에서 사용되어 온 기술이다.딥러닝이 발전하게 된 이유New computational power 딥러닝은 계산 비용이 많이 든다. 예를 들어 코드를 병렬화
12.Lecture 12
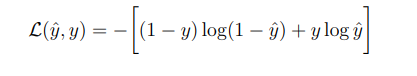
본 강의는 이전강의인 Lecture 11과 이어지는 내용이므로 참고 해주시길 바랍니다.훈련 과정 중 foward propagation이 진행되고 나면, 우리는 결과값 $\\hat{y}$을 얻게 된다. $\\hat{y}$ 값을 얻으면 이제 비용함수를 계산한다.비용함수를
13.Lecture 13
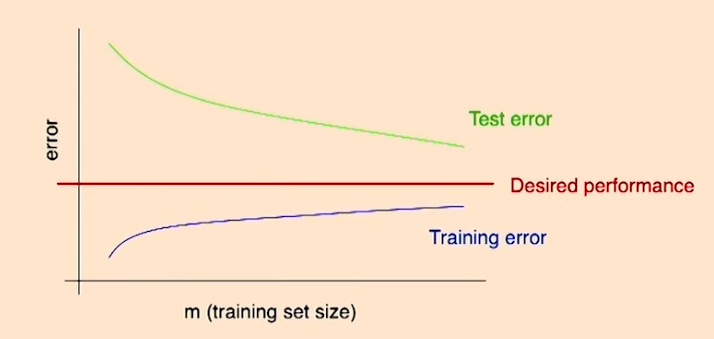
프로젝트를 진행하거나 프로그램을 돌리다 보면 여러가지 오류가 발생하는 경우가 많다. 프로젝트를 진행할 때 종종 ‘많은 양의 데이터를 사용하는 것이 시간을 잘 활용한다는 확신이 없다면 시간낭비를 하지 말아라’ 라는 조언을 듣기도 한다. 즉, 우리가 원하는 알고리즘을 만들
14.Lecture 14
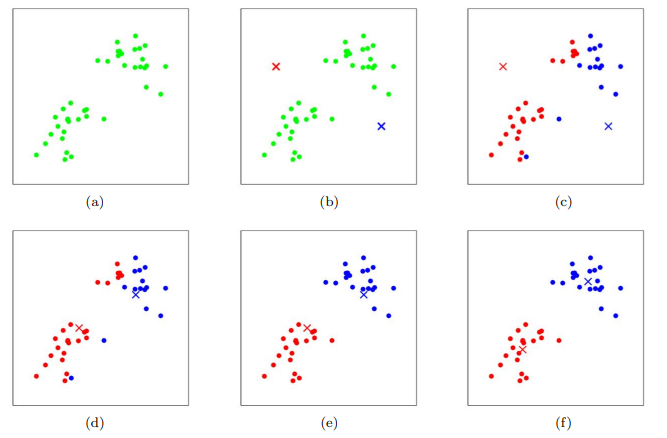
클러스터링은 비지도 학습 중 하나이다. 데이터 x가 주어질 때, 데이터를 그룹으로 묶는 알고리즘 이며 주로 Market Segmentaion에 사용된다. Untitled!\[](https://velog.velcdn.com/images/sgu20191619/p
15.Lecture 15
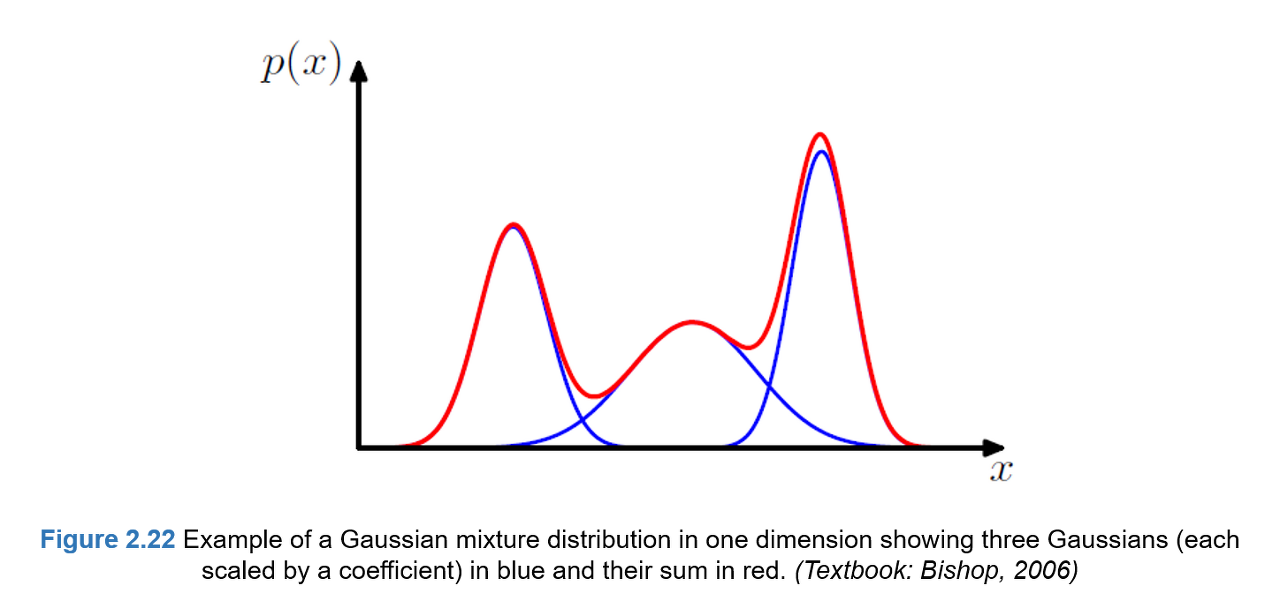
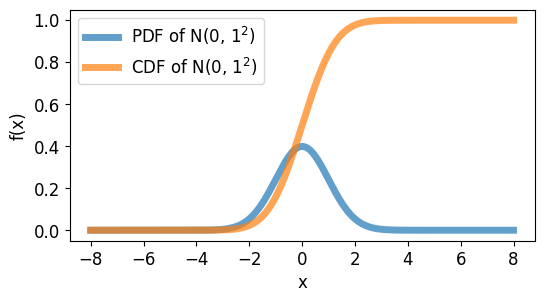
들어가기에 앞서 Lecture5, Lecture 14, 가우시안 분포와 밀도, 기타 통계학 지식을 요합니다.여러 개의 가우시안 분포들의 선형 결합으로 실제데이터의 분포를 근사하는 방법으로 아래와 같은 그림으로 표현할 수 있다.단일 가우시안 분포를 통해 데이터 분포를 표
16.Lecture 16
ICA는 대표적으로 Cocktail party problem에 적용되는 모델이다. 파티에서는 여러 소리가 섞이기 마련인데, 이 소리들을 어떻게 분리하여 원래 소리를 추정할 수 있는지에 대한 알고리즘이다. 예를 들어 방에서 음악소리를 S1, 대화소리를 S2라고 하고 이를
17.Lecture 17
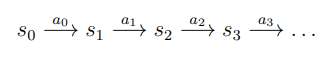
본 강의는 이전 강의였던 Lecture 16의 끝부분과 이어지는 내용이다. 강화학습이란 시행착오를 통해 학습하는 방법이다. 이전의 지도 학습의 경우 정답이 정해져 있는 반면 강화학습의 경우에는 보상을 통해 가중치와 편향을 학습하는 방법이다. Markov decisi
18.Lecture 18
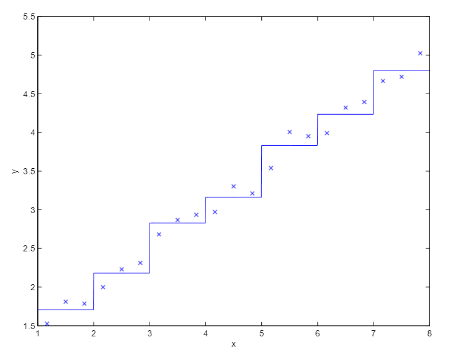
여태까지는 유한한 상태의 MDP에 대해 알아보았다면, 이제는 무한한 상태, 즉 연속적인 상태의 MDP에 대해 알아보자예를 들어, 자동차의 경우 자동차에는 무한한 경우의 위치가 있기 때문에 state의 개수가 무한하다고 할 수 있다. \*\*\*\*이 때, MDP를 어떻
19.Lecture 19
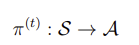
Finite-horizon MDP의 구성 요소: <T,S,A,P,R>T: length of the horizonS: set of states (state space)A: set of actions (action space)p: state probabilityR:
20.Lecture 20

이번 강의는 Lecture 13의 헬리콥터 예제를 다시하번 살펴보는 것부터 시작한다. 저번에는 강화학습을 배우지 않고 예제를 활용했던 반면, 강화학습을 배우고 난 후 실제로 RL debugging diagnostics가 어떻게 활용되는지 살펴보자.업로드중..헬리콥터 시
21.CS229

이 시리즈는 deep.daiv 동아리에서 팀으로 활동했던 내용을 . http://deepdaiv.com/