deep.daiv 동아리에서 진행했으며 팀원과 함께 정리한 내용입니다.
Lecture 3
Probabilistic interpretation
확률적 해석을 하는 이유!
“cost function J가 왜 최소 제곱의 합의 꼴인가에 대한 유도를 하기 위해 “
What is Probability Distribution?
확률 분포란: 수집 및 관측된 데이터의 발생 확률을 잘 근사하는 분포
보통 p(x∣θ)로 표현한다.
∗∗θ 추정의 목적**: 데이터의 실제 확률 분포를 최대한 잘 근사하는 수학적 모형을 찾는것
모델 표현하는 확률 분포를 데이터의 실제 분포에 가깝게 만드는 최적 파라미터 값 찾기
yi=θTxi+ϵi 라고 가정할 때 ϵi=error, unmodeled effects, random noises이다.
ϵ∼N(0,σ2) (정규분포, 가우스분포)
p(ϵi)=(2πσ)1exp(2σ2−ϵ2) (엡실론 i의 확률밀도)
p(yi∣xi;θ)=(2πσ)1exp(2σ2−(yi−θTxi)2) (yi−θTxi=+ϵi)
(ex: x와 theta가 주어졌을 때, 특정 주택 가격의 확률)
(θ에 의해 매개변수화 되었고 x가 주어졌을 때 y의 확률밀도)
Maximum Likelihood Estimation (MLE)
📢 **Likelihood VS Probability:**
가능도: 데이터는 고정이고, parameter가 변수로 움직이면서 변화한다.
확률: 매개변수는 고정이고, Y값에 대한 확률
- 관측된 데이터 X=(x1,x2,x3,...,xn)를 토대로 상정한 확률 모형이 데이터를 잘 설명하도록 하는 θ를 찾는 방법
- n개의 관측된 데이터의 발생 확률이 전체적으로 최대가 되도록 하는 parameter를 찾는 방법
L(θ)=L(θ;X,y)=p(y∣X;θ)
L(θ)=∏i=1mp(yi∣xi;θ)=∏i=1m(2πσ)1exp(2σ2−(yi−θTxi)2) (목표는 L(θ) 를 최대화 시키는것!)
(위의 식에서 각각의 데이터 발생사건이 독립적으로 발생한다고 가정한다.)
→ likelihood function은 곱의 꼴이기 때문에 log를 취해 더하는 꼴로 변경 (또한 확률의 곱은 기하급수적으로 작아지기 때문에 더하는 꼴로 변경한다.)
l(θ)=logL(θ)=log∏i=1m(2πσ)1exp(2σ2−(yi−θTxi)2)=∑i=1m(2πσ)1exp(2σ2−(yi−θTxi)2)
(2πσ)mlog−σ21×21∑i=1m(yi−θTxi)2
위의 함수를 최대화 시키기 위해서 21∑i=1m(yi−θTxi)2를 최소로 만들어야 한다.
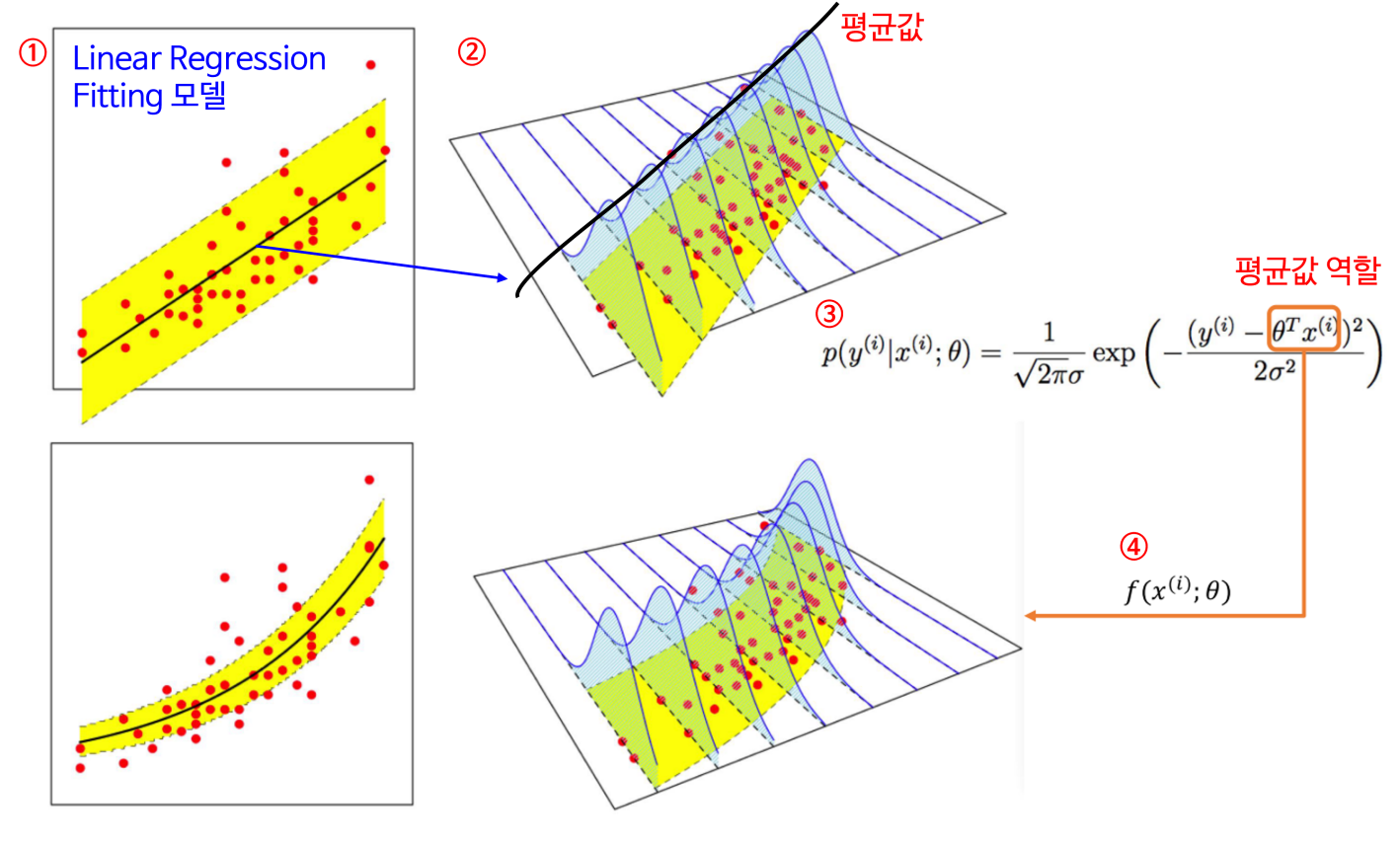
머신러닝의 확률적 해석에 대한 그림
∗∗21∑i=1m(yi−θTxi)2는 J(θ)꼴로 왜 cost function이 제곱의 합 꼴인지 알아보았다.**
Locally weighted linear regression
📢 Parametric Model VS Non-Parametric Model
Parametric Model: 고정된 개수의 파라미터를 학습한다.
Non-Parametric Model: 학습 데이터가 늘어남에 따라 파라미터의 개수도 늘어난다.
Locally weighted linear regression은 Non-Parametric Model에서 주로 쓰인다.
왜 국소 가중 회귀가 필요한가?
좁은 범위의 비 선형 데이터를 선형데이터로 해석하여 목표하는 점 근처의 값으로만 계산한다.
Linear Regression: Fit θ to minimize costfunction=J(θ)=21∑i=1m(yi−θTxi)2
Locally weighted regression: Fit θ to minimize ∑i=1mwi(yi−θTxi)2 (w=weight function)
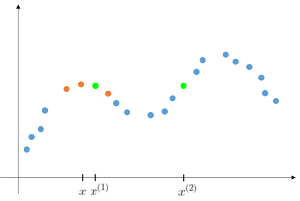
wi=exp(2−(xi−x)2)
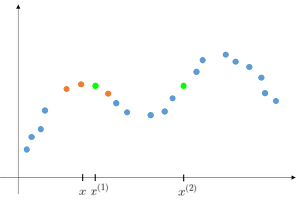
if ∣xi−x∣ is small, xi≈1
if ∣xi−x∣ is larger, xi≈0
x1−x의 값이 작으므로 w는 1에 가까워지고
x2−x의 값은 크므로 w는 0에 가까워져서
예측을 위한 데이터에서 제외된다.
x로부터 가까이 위치한 값만 데이터에 이용
Bandwidth Parameter tau(τ)
x값으로부터 얼마다 가까운 데이터만 이용할 지 결정하는 parameter
wi=exp(2τ2−(xi−x)2)
Locally weighted linear regression: feature이 2,3개로 적지만 많은 데이터를 가지고 있을 때 주로 사용
Logistic regression
- Classification 모델로서 사용되는 회귀이다.
- binary classification에서 y값은 오직 0 또는 1을 가진다.
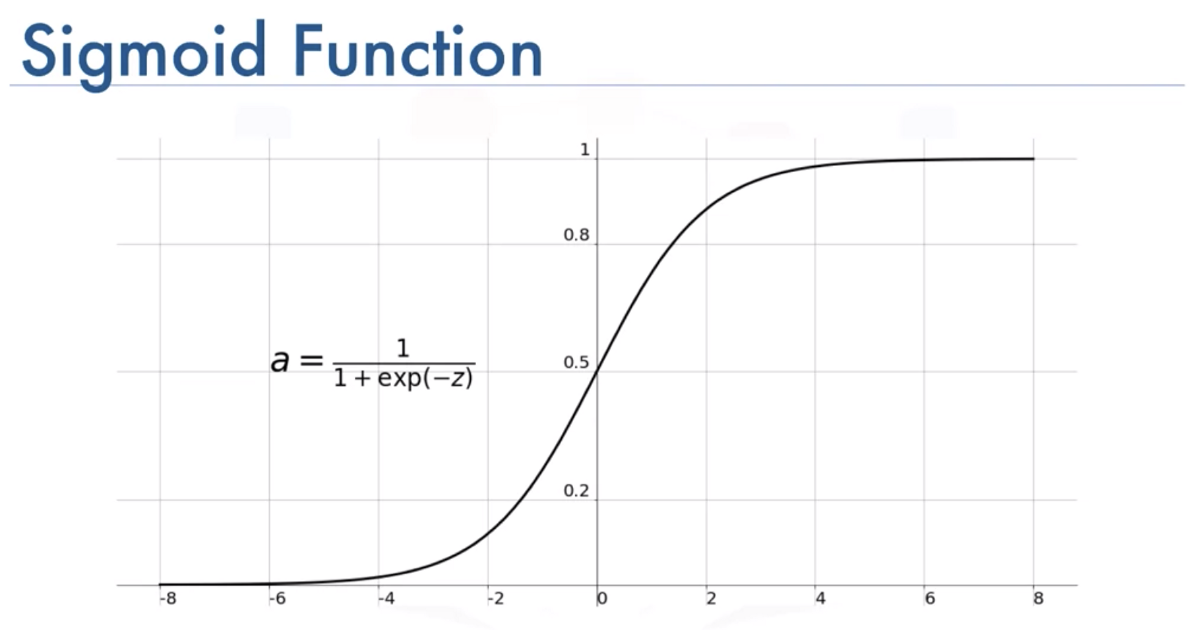
hθ(x)∈[0,1] , hθ(x)=g(θTx)=1+e−θTx1 , g(z)=1+e−z1
g(z)= logistic function or sigmoid function
p(y=1∣x;θ)=hθ(x) (ex: 종양의 크기를 고려할 때 y=1일 확률)
p(y=0∣x;θ)=1−hθ(x) (ex: 종양의 크기를 고려할 때 y=0일 확률)
한 개의 식으로 압축했을 때: p(y∣x;θ)=hθ(x)y(1−hθ(x))1−y
선형회귀에서 maximum likelihood estimation을 사용한 것처럼 로지스틱 회귀에서도 MLE를 사용하도록 한다. ( 가장 확률을 높이는 parameter를 구하기 위해서)
L(θ)=p(y∣X;θ)=∏i=1mp(yi∣xi;θ)=∏i=1mhθ(x)y(1−hθ(x))1−y
l(θ)=logL(θ)=∑i=1myi×logh(xi)+(1−yi)log(1−h(xi))
Goal: choose θ to maximize l(θ) 이므로 l(θ)를 미분한다.
∂θj∂l(θ)=(y×g(θTx)1−(1−y)1−g(θTx)1)∂θj∂g(θTx)
(y×g(θTx)1−(1−y)1−g(θTx)1)g(θTx)(1−g(θTx))∂θj∂θTx
by g′(z)=dzd1+e−z1=(1+e−z)21×e−z=1+e−z1(1−1+e−z1)=g(z)(1−g(z))
=(y(1−g(θTx)−(1−y)g(θTx))xj=(y−hθ(x))xj
Stochastic gradient descent 의 꼴과 같다고 할 수 있다.
θj:=θj+α(yi−hθ(xi))xji
logistic regression
θj:=θj+∂θj∂l(θ) (l(θ)를 최대화 시켜야하기 때문에 부호가 양수)
gradient descent
θj:=θj−∂θj∂J(θ) (J(θ)를 최소화 시켜야 하기 때문에 부호가 음수, 기울기가 양수라면 음의 방향으로 옮겨야 하고, 기울기가 음수라면 양의 방향으로 옮겨야 최소가 나온다.)
Newton’s Method
gradient descent를 통해서 수렴하기 위해 많은 iteration이 필요
그러나 Newton’s Method를 활용하면 적은 iteration을 통해서도 수렴에 도달할 수 있다.
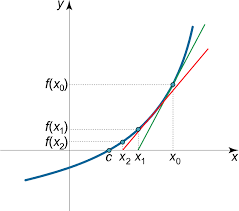
Goal: f(θ)=0인 θ를 구하는 것
위의 로지스틱 회귀에서 l(θ)를 최대시키려고 했다.
그 결과 l′(θ)=0인 θ를 구하는 문제로 변경되었다.
θ:=θ−f′(θ)f(θ) 이를 다시 변환하면 θ:=θ−l′′(θ)l′(θ)
위의 경우는 θ가 실수인 경우이고 θ가 벡터일 때: θ:=θ−H−1∇θl(θ)
H를 Hessian matrix라고 한다. Hij=∂θi∂θj∂2l(θ)라고 할 수 있다.
Newton’s method의 단점: 고차원 문제(feature가 많을 때)에서 과정에 비용이 많이 든다.
매개변수의 개수가 적다면 Newton’s method를 쓰는 것이 압도적으로 유리하다.