Lecture 20

리치·2023년 5월 21일

CS229

목록 보기

20/21

Lecture 20

RL debugging Diagnostics

이번 강의는 Lecture 13의 헬리콥터 예제를 다시하번 살펴보는 것부터 시작한다. 저번에는 강화학습을 배우지 않고 예제를 활용했던 반면, 강화학습을 배우고 난 후 실제로 RL debugging diagnostics가 어떻게 활용되는지 살펴보자.

💡 **자율주행 헬리콥터**

헬리콥터 시뮬레이터를 만든다.
Reward function을 설정한다.
이때 Reward funciton 은 $R(s) = \vert\vert s-s_{desired}\vert\vert^2, s=helicopter \ position$
$E[R(s_0) + R(s_1) + \dots +R(s_T)]$ 의 최대값을 갖게하는 강화학습 알고리즘을 실행하여 헬리콥터가 시뮬레이터 안에서 원활하게 작동하도록 한다.
이렇게 얻은 매개변수 $\pi_{RL}$ 은 인간의 조종보다 훨씬 떨어지는 성능을 가지고 있다. 즉 $\pi_{RL} < \pi_{human}$

Debugging an RL algorithm

정책 $\pi_{RL}$ 이 실제 환경에서 정상적으로 작동하기 위해서는 다음과 같은 가정이 필요하다.

헬리콥터 시뮬레이터가 정확하다. 즉, 시뮬레이터에서 잘 작동한다면 실제 환경에서도 잘 작동한다.
강화학습 알고리즘이 $E[R(s_0) + R(s_1) + \dots +R(s_T)]$ 를 최대화 시키며 정확하게 헬리콥터를 조종할 수 있다.
보상값을 최대화 시키는 것은 자율주행의 성공을 뜻한다.

위와 같은 가정을 만족한다면, 다음과 같은 workflow를 통해 debugging 할 수 있다.

만약 $\pi_{RL}$ 이 시뮬레이터에서 잘 작동하지만, 현실에서는 작동하지 않는다면, 문제는 시뮬레이터에 있다.
만약 $V^{\pi_{RL}}(s_0) < V^{\pi_{human}}(s_0)$ 라면, reward function을 최대화 하는데는 성공하였기 때문에 강화학습 알고리즘에 문제가 있다는 것이다.
만약 $V^{\pi_{RL}}(s_0) > V^{\pi_{human}}(s_0)$ 라면, reward funciton에 문제가 있다는 것이다.

이번 내용은 Debigging an RL algorithm 의 내용과 이어지는 부분이 많아, Lecture 13을 보고 이번 강의노트를 본다면 이해하는데 훨씬 더 많은 도움이 된다.

Direct policy search

이전에 배웠던 강화학습들은 모두 indirect한 방법으로 정책을 찾았다. 예를 들어 value function을 찾고 value function을 통해 정책을 찾는 방법이 있다. 하지만 이번에는 정책을 한번에 찾는 방법에 대해 소개하고자 한다.

Inverted pendulum(역립진자) 예제

역립진자란 질량은 위에 있고 진자는 아래쪽에 있는 형태의 진자를 뜻한다. 즉, 직자의 축이 수직으로 서있게 하기 위해서는 진자가 무게중심을 찾으며 끊임없이 좌, 우로 움직여야 한다. 이해하기 쉽게 설명하자면, 손바닥 위에 막대기를 놓고 중심을 잡는 과정과 유사하다고 생각하면 된다.

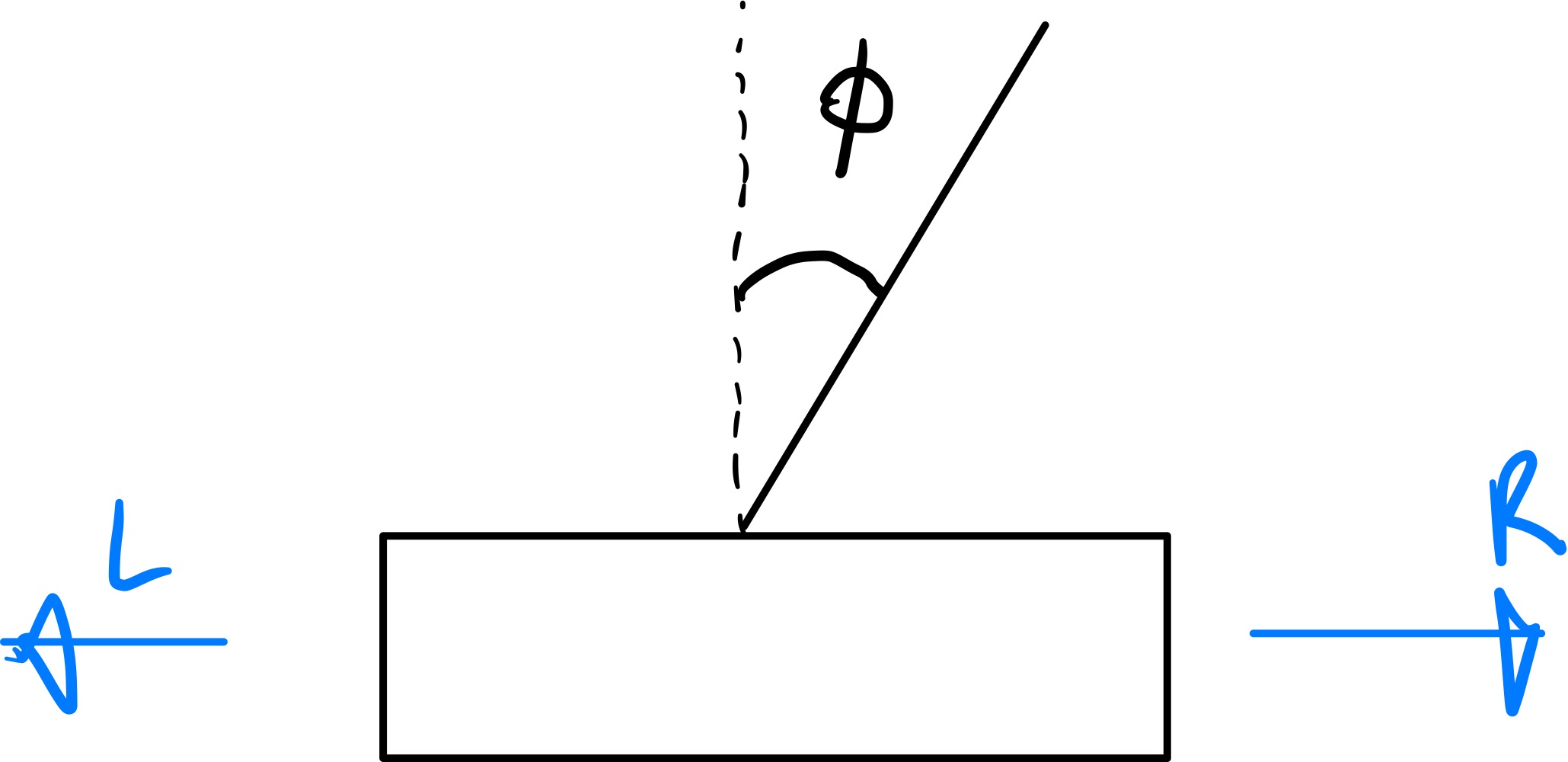
이렇게 진자의 위치, 속도, 각도, 각속도를 state로 정한다. direct policy의 핵심적인 아이디어는, 이전 강화학습 알고리즘 처럼 action의 확률이 이산적인 분포가 아닌, 연속적인 분포를 가지고 있다는 것이다. 따라서 위의 예제의 경우에 다음과 같은 정책을 사용할 수 있다.

\Pi_\theta(s) = \frac{1}{1+e^{-\theta^Ts}} \\

또한 state와 action의 값을 에를 들어 설정해 본다면,

s= \begin{bmatrix}position \\ velocity \\ angle \\ angular \ velocity\end{bmatrix}, \theta^T = \begin{bmatrix} 0 \\ 0\\ 1 \\0\end{bmatrix}

오른쪽으로 이동하는 action을 취하는 정책의 값은 다음과 같아질 것 이다.

\Pi_\theta(s,R)= \frac{1}{1+e^{-\phi}}

시그모이드 함수의 그래프를 생각해보면, 진차축의 각도 $\phi$ 가 커지게 되면, 시그모이드의 함수값 또한 커지게 된다. 즉 진자는 중심을 잡기위해 오른쪽으로 이동할 확률이 1에 가까워 진다는 것이다.

Maximizing Expectation

Direct policy의 최종목표는 위의 예시처럼 진자축의 각도 뿐만 아니라, 여러가지 요소들에 대해 적절한 $\theta$ 를 대입하며 expextation을 최대화 하는 것이다. 수식을 통해 정리해보도록 하자.

max \ E[R(s_0,a_0) + R(s_1,a_1)+\dots +R(s_t,a_t)] \vert \pi_\theta \\ = max \sum_{s_0a_0s_1a_1} P(s_0,a_0,s_1,a_1) \times[R(s_0,a_0) + R(s_1,a_1)]\\ = max \sum_{s_0a_0s_1a_1} P(s_0,a_0)\pi_\theta(s_0a_0)P_{s_aa_0}(s_1)\pi_\theta(s_1,a_1)\times[R(s_0,a_0) + R(s_1,a_1)]

Expectation의 최대값을 얻기 위해서는 미분을 통한 경사상승법을 통해 구할 수 있다. 실제 알고리즘이 어떤지 살펴본 후, 왜 알고리즘이 expaction을 최대화 하는지 살펴보도록 하자.

Reinforce algorithm

Reinforce algorithm을 수식으로 표현하면 다음과 같다.

Loop: [sample (s_0,a_0,s_1,a_1, \dots , s_t,a_t), \\ compute\ payoff: R(s_0,a_0) + R(s_1,a_1)+\dots +R(s_t,a_t) \vert \pi_\theta \\ \\ \theta : \theta + \alpha\frac{[\nabla_\theta\pi_\theta(s_0,a_0)}{\pi_\theta(s_1,a_1)} + \frac{[\nabla_\theta\pi_\theta(s_0,a_0)}{\pi_\theta(s_0,a_0)}\times [R(s_0,a_0) + R(s_1,a_1)]

Reinforce algorithm은 이전 state, action, payoff에 따라 현재의 매개변수 $\theta$ 의 값이 달라지기 때문에 확률적 경사상승 알고리즘의 성향을 띈다. 하지만 이전 선형회귀에서 사용했던 확률적 경사상승 알고리즘과는 다르게 매개변수의 업데이트 값들은 평균적으로 gradient 방향을 향하게 된다. 왜 그렇게 되는지 알아보도록 하자.

앞서 expectation의 최대값을 구하려면 미분을 해야한다고 했다. 따라서 미분을 진행해 보면