Lecture 19

Finite-horizon MDPs

---

• Finite-horizon MDP의 구성 요소: <T,S,A,P,R>

T: length of the horizon

S: set of states (state space)

A: set of actions (action space)

p: state probability

R: reward function

• 행동이 시간에 따라 달라질 수 있다는 점이 finite-horizon mdp의 특징이다.
• optimal policy가 시간에 따라 변하기 때문에 non-stationary policy이다.

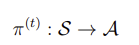
• payoff의 정의를 다음과 같이 정의할 수 있다. 원래는 discounting factor 감마를 표시했으나 finite horizon mdp에는 없다.

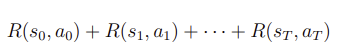
• time dependent dynamics라는 표현을 쓰곤 한다. transition의 분포인 $P_{s_t,a_t}$가 시간에 따라 변한다.

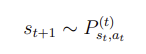
Optimal value function

시간이 얼마나 남아있느냐에 따라서 어떤 선택을 할 지가 달라진다.

예를 들어, reward가 +1인 것과 +10인 것이 있을 때, 당연히 시간 제약이 없다면 +10을 선택해야겠지만 시간 제약이 있을 때, +10으로 향하는 step의 시간이 걸린다면 +10을 선택하는 것보다 바로 가까이 있는 +1을 선택하는 것이 더 좋은 선택이다.

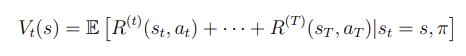
이 때, value iteration을 하게 되면, Dynamic programming algorithm과 같다.

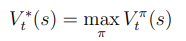
1. 마지막 state에서 시작한다. 마지막 state에는 다음 action과 stage가 없기 때문에 value function은 immediate reward이다.

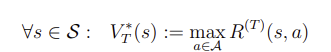
1. t=T-1에서 t를 하나씩 빼가면서 거꾸로 따라간다.

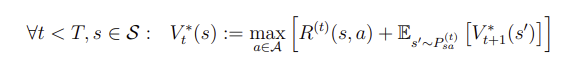
Linear Quadratic Regulation (LQR)

---

small set of problems에 주로 적용한다.

Linear quadratic regulation을 하기에 앞서 모델의 가정을 하고자 한다.

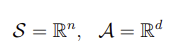
그리고 선형 상태를 가정하고자 한다. (noise와 함께)

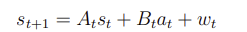
그리고 Linear Quadratic Regulation의 보상은 다음과 같은 형식으로 주어진다.

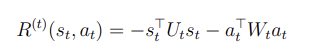
$U\in R^{n*n}$,$W\in R^{d*d}$이고, $U,W$는 0보다 크기 때문에

$S^TUs$도 0보다 크거나 같고, $a^TWa$도 0보다 크거나 같다.

State를 알고 싶다면 state vector가 0에 가까워야한다. (Reward가 커지는 방향)

이 때, U와 W를 항등행렬 I로 둔다. 그러면 이 때, $R=-||s||^2-||a||^2$로 바뀌어진다.

지금까지는 LQR algorithm을 하기 위한 가정들에 대해 알아보았고

이제는 행렬 A,B를 어떻게 구하는지에 대해 알아보자

1. $S_{t+1}\sim AS_t+BS_t$이기 때문에 다음과 같은 과정(선형회귀에서 최소 제곱법과 비슷한 과정)을 하면 A,B를 구할 수 있다.

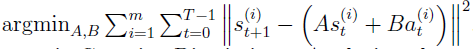
1. 비선형 모델을 선형화하는 것

강의에서 언급한 inverted pendulum의 예를 들면, 다음과 같은 관계식을 세울 수 있다.

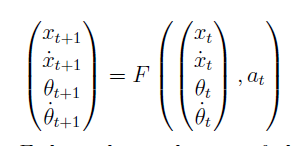
앞선 강의에서 언급한 Newton’s method를 쓰면 $s_{t+1}$를 다음과 같은 식으로 근사할 수 있다.

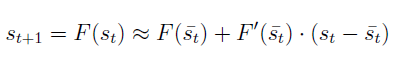
그런데 위 식은 편의를 위해 a에 대한 식을 없앤 것이기 때문에 일반적인 경우에는 a가 포함된 다음과 같은 식으로 나타낼 수 있다.

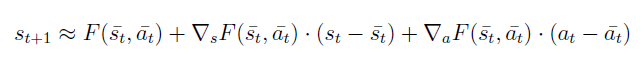
위의 식을 약간 변형하면 $s_{t+1}=A_t*s_t+B_t*a_t$로 변형할 수 있으므로 결국 행렬 A,B를 구할 수 있다.

Dynamic Programming (LQR)

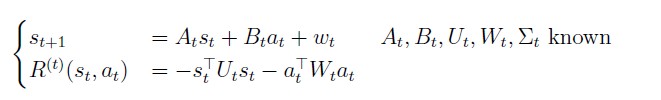
다음과 같은 조건이 주어진다.

Optimal value function V star를 계산하기 위한 dynamic programming algorithm을 사용할 것이다.

위의 Finite horizon mdp의 dynamic programming과 유사하게 시작을 한다.

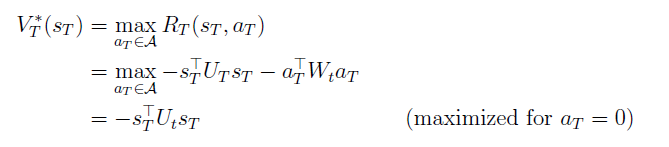
immediate reward를 maximize하는 방향으로 action을 선택한다.

$V^*_{t+1}$를 알고 있다고 가정할 때, $V^*_{t+1}$는 quadratic function이므로, $V^*_{t}$또한 quadratic function이라고 할 수 있다.

그리고 다음과 같은 가정을 한다.

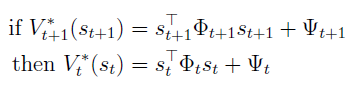
여기서 phi와 psi는 그냥 행렬과 스칼라이다.

아래 식의 두번 째줄은 optimal value function의 정의이고, 세번 째 줄은 quadratic assumption을 통해 변형한 식이다.

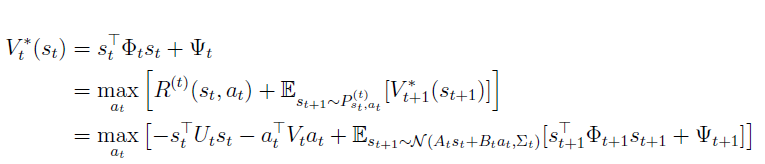
세번 째 줄의 표현은 optimal action의 quadratic function으로 변경할 수 있어서 다음과 같은 식으로 변형할 수 있다. action에 대해 derivation을 하고 미분한 값이 0이 되게 하면 다음과 같은 식이 나온다….

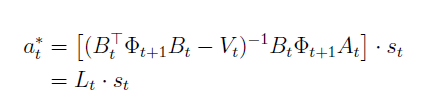
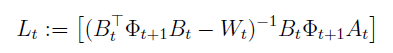
Optimal action is a linear function of the state이라고 할 수 있다.

approximation이 아니라 바로 선형식으로 나올 수 있다는 것이 장점이다.

그리고 위의 식을 풀게 되면 psi와 phi에 대한 식이 나온다.

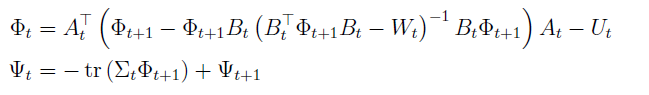
sigma는 sum이 아니라 공분산을 의미한다.

여기서 알 수 있는 점은 $\phi_t$는 noise와 $\psi$와 관련이 없다는 것이다. 그리고 optimal policy 또한 noise와 관련이 없다는 것이다. sigma는 psi와만 연관이 있다. 그래서 V_star은 sigma와 연관이 있다.

Summarize를 하기 위해서 다음과 같은 작업을 한다.

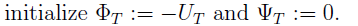
이제 iteration을 진행한다. t=T-1에서부터 거꾸로 시작해서 psi와 phi를 구한다.