이 과제를 통해 벡터를 처음 접하였기에 개념적인 부분을 이해하는데 시간을 많이 쏟았다.

개요

miniRT는 인자로 주어지는 파일에 3차원 상의 공간에 카메라, 광원, 물체들이 어느 좌표에서 어느 지점을 바라보고 있는지(벡터)에 대한 값밖에 주어지지 않는다. 애초에 과제에서도 대놓고 드러내고 있지만, 벡터라는 개념을 이용해서 우리는 3차원 공간 상의 점의 위치, 방향을 수학적으로 계산하여 이미지를 구현할 것이다.

벡터의 개념

벡터는 수학, 과학, 물리학, 공학, 프로그래밍 등 여러 방면에서 사용되는 개념이다. 그러나 기본적으로 공유하고 있는 개념은 크기, 방향을 가지고 있다는 것이다.

• 속력 : 크기 / 시속 100km
  • 스칼라
• 속도 : 크기 + 방향 / 시속 100km로 동쪽으로 달렸다
  • 백터

크기와 방향을 갖는 양을 벡터라고 한다.

화살표를 이용하면 크기와 방향을 전부 표현할 수 있다.

• 길이 → 크기
• 방향 → 방향

벡터가 시작하는 점을 시점, 끝나는 점을 종점이라고 한다.

---

백터의 길이

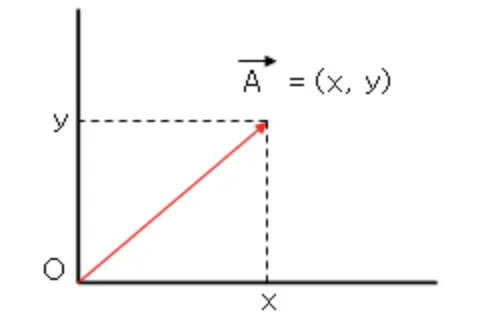
기하학적으로 벡터의 크기는 방향을 가진 선분의 길이이다. 벡터의 성분이 주어졌다고 할 때, 우리는 피타고라스 정리를 활용해 벡터의 크기를 알 수 있다! (|A| 는 벡터 A의 크기를 나타낸다)

직각삼각형의 빗변의 제곱은 다른 두 변의 제곱을 더한 것과 동일하다. 여기서 루트를 씌워서 제곱근을 없애면 빗변의 길이, 벡터의 길이를 알 수 있게 된다.

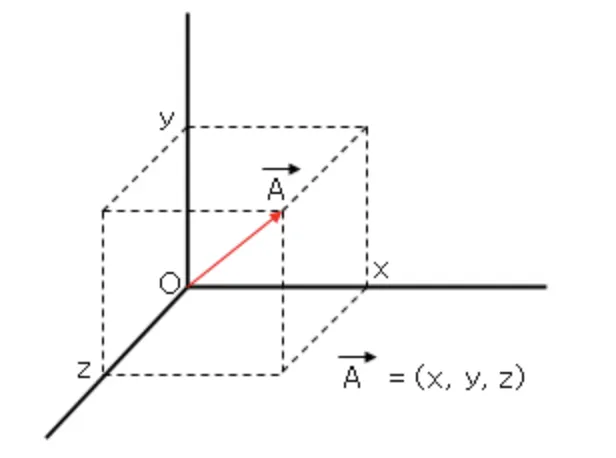
3차원 벡터도 위의 방식을 사용하면 어렵지 않게 표현할 수 있다.

벡터의 크기와 방향 복습 (개념 이해하기) | 벡터 | Khan Academy

---

단위 백터

**단위벡터 (Unit Vector) = 방향 벡터**

백터의 단위가 1일 경우 단위 백터라고 한다.

크기가 항상 1로 고정되어 있기에 방향을 나타내는데 집중되어 있다고 할 수 있다.

단위 벡터는 크기는 1이지만 방향을 가지고 있으므로, 여기에 값을 곱해주면 방향은 같지만 크기가 다른 벡터를 마음대로 만들 수 있다. 혹은 크기는 무시하고 방향만 나타내기 위해서 사용한다.

모든 벡터는 정규화(normalize) 과정을 거쳐 단위 벡터로 만들 수 있다. 벡터 U를 (x, y)라고 했을 때, 정규화를 하는 식은 아래와 같다.

위 식은 벡터의 각 성분에 벡터의 크기(길이, 스칼라)를 나눠준 것이다!

---

영백터

시점과 종점이 똑같은 백터를 영백터라고 한다.

방향을 고려하지 않기에 백터의 조건을 충족하지는 않지만 크기가 0이기에 영백터라고 부른다.

---

역백터

크기는 같고 방향이 정 반대인 벡터, 백터의 시작점과 종점이 바뀐 것을 의미한다.

A 벡터의 역벡터는 -A벡터이다!

---

법선 백터

**법선벡터 (Normal Vector)**

법선벡터는 어떤 표면(평면)에 수직인 뱡항으로 뻗어나가는 벡터이다.

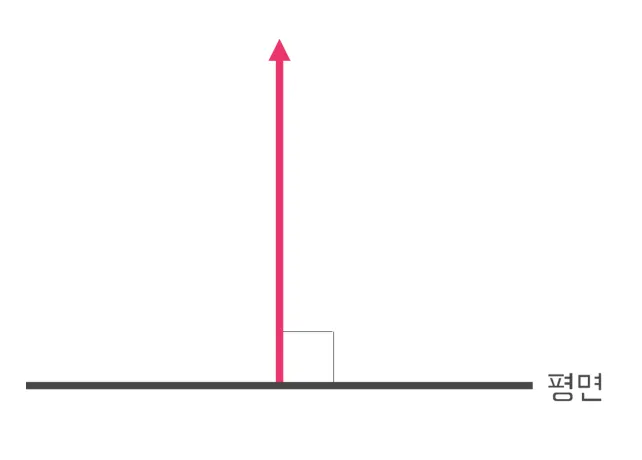
컴퓨터 그래픽스에서는 모든 Normal Vector(법선벡터)를 Unit Vector(단위벡터)로 표현한다. 특정 벡터(1, 2, 2)에 벡터의 길이(3)를 구하고 각 요소에 길이를 나눠주는 것(1 / 3, 2/ 3, 2 / 3)으로 구해줄 수 있다.

---

동일한 백터

크기, 방향이 동일하다면 위치에 상관없이 두 벡터는 같은 백터라고 볼 수 있게 된다.

크기는 같지만 방향이 정반대인 경우 -를 붙인다.

https://www.youtube.com/watch?v=g3n1VxiXgrE

---

백터의 덧셈

벡터의 덧셈은 그림으로 보면 엄청 간단하다.

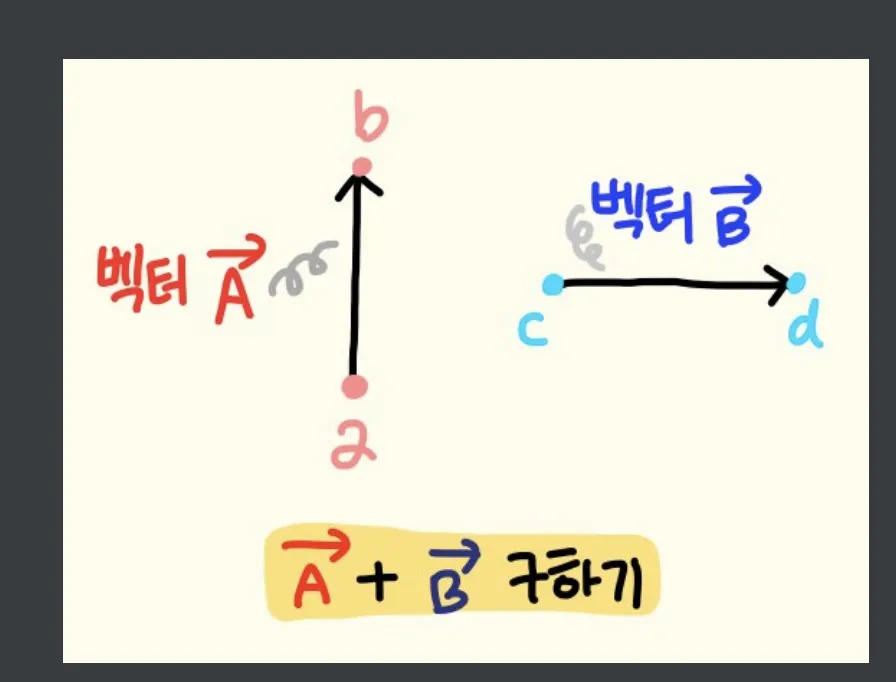
출처 : https://ansohxxn.github.io/c++ games/chapter3-2-1/

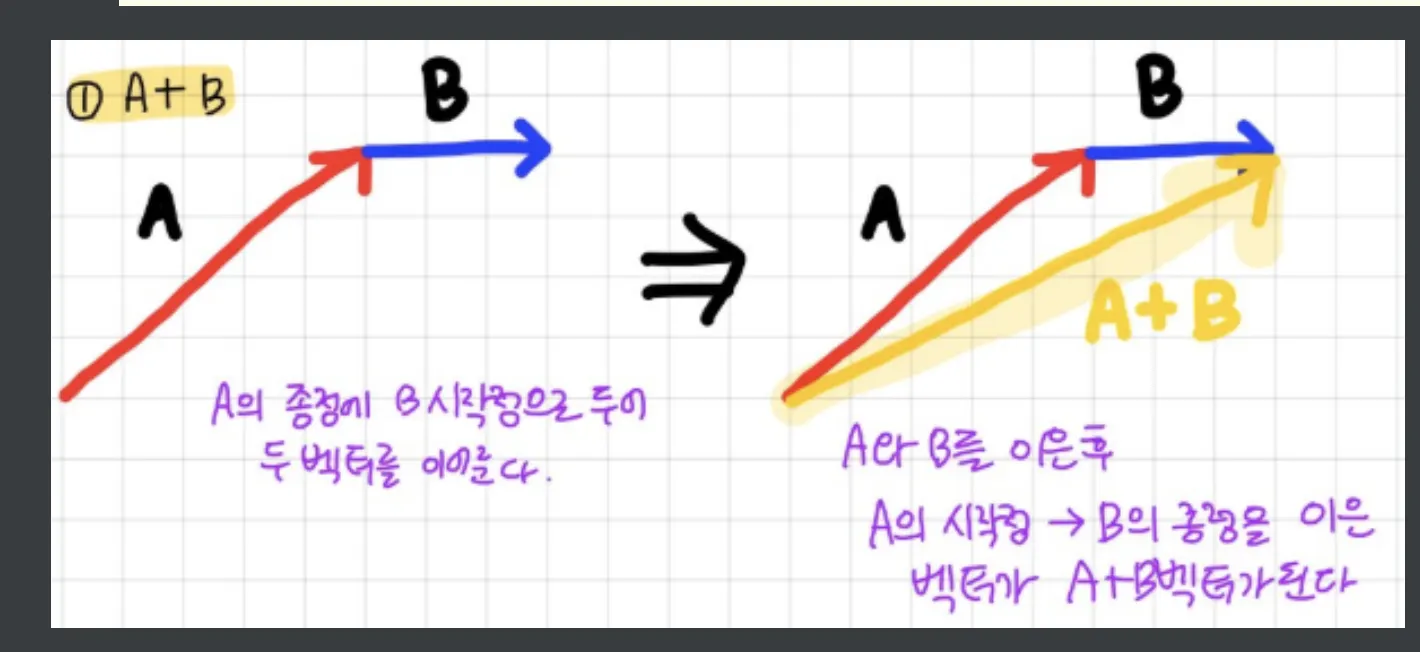
출처 : https://ansohxxn.github.io/c++ games/chapter3-2-1/

**어디서 사용할까?**

• 좌표를 이동시킬 때 많이 사용된다!

2차원 좌표

• 크기와 방향이 동일하다면 시점, 종점이 다르더라도 동일한 백터로 볼 수 있다는 것을 위에서 알았다. (믿기지 않는다면 벡터를 평행 이동한다고 생각해보아라!)
• 벡터의 덧셈은 한 벡터의 시점이 원점(0, 0, 0)이 아닌 다른 벡터의 종점에서 출발하는 것과 같다고 볼 수가 있다.

**벡터의 뺄셈**

A벡터 - B벡터는 A벡터 + (-B)벡터와 같다! -B벡터는 위에 나온 역벡터이다.

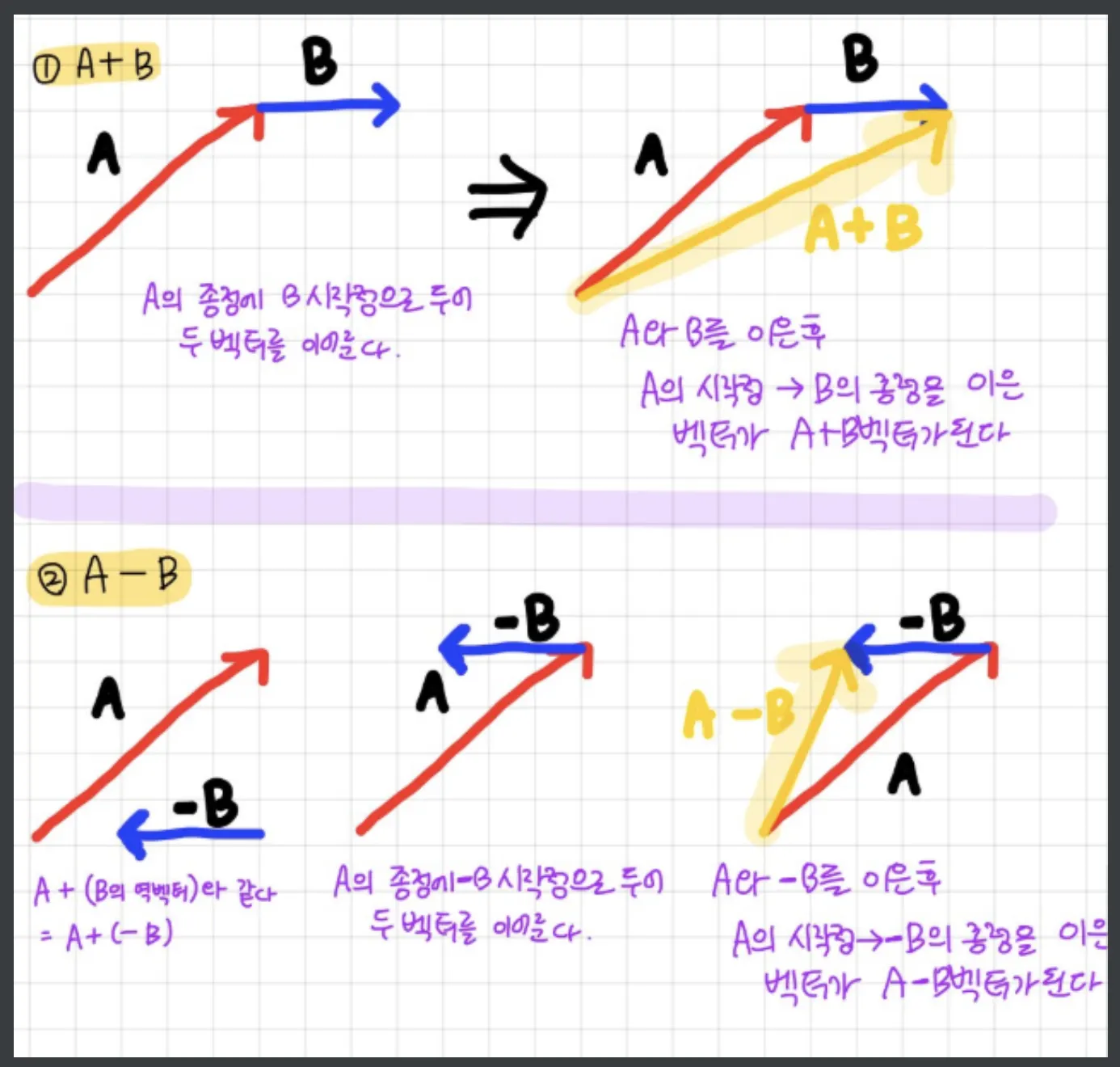
출처 : https://ansohxxn.github.io/c++ games/chapter3-2-1/

2차원 좌표

덧셈과 동일하면서도 조금 다르다. 뺄셈이기에 빼는 벡터는 역벡터가 되어서 빼는 대상이 되는 벡터의 종점을 시점으로 하여서 전진한 종점이 결과가 된다.

---

백터의 내적

실수(스칼라) 값이 나온다.

벡터의 내적의 정의는 한 벡터의 종점에서 다른 벡터에 수선의 발을 내린 후에 형성되는 직각삼각형의 밑변의 길이와 다른 벡터(B)의 길이를 곱한 값이다. 그림으로 표현하면 아래와 같다.

이를 수식으로 표현하면 다음과 같다.

cosθ는 x / y고 A의 길이는 x와 동일하기에 위의 수식을 이렇게도 쓸 수 있을 것이다.

이를 한 번 더 정리하면 최종적으로 다음과 같은 꼴이 된다.

내적의 특징

동일한 벡터의 내적은 벡터의 길이의 제곱

내적의 특징으로 동일 한 벡터가 있을 경우에는 두 벡터가 이루는 각은 0도이므로 cos0 = 1. 그러므로 벡터 a의 절대값( 길이 )의 제곱이 되는것을 알 수 있다.

단위 벡터 끼리의 내적은 두 벡터 간 각도의 코사인

결과값이 0이라면, 두 벡터는 직각이다.

결과값이 0보다 크다면 두 벡터간 각도의 θ는 예각이다.

결과값이 0보다 작다면 두 벡터간 각도의 θ는 둔각이다.

단위 벡터와의 내적은 벡터의 종점에서 발을 내렸을 때 형성되는 삼각형의 밑변과 동일

위의 예제에서 만약 벡터 B가 단위 벡터라고 해보자. 단위 벡터는 길이는 항상 1이다. 그렇다는 것은 내적을 했을 때 나오는 결과인 y * 벡터 B의 길이에서 벡터 B의 길이를 생략해주어도 아무런 문제가 없어진다.

즉 단위 벡터 B와 내적한 결과는 벡터 A의 종점에서 아래로 수선을 내렸을 때 형성되는 삼각형의 밑변 y가 된다는 의미가 된다.

[3D 게임 프로그래밍을 위한 기초 수학] 3. 벡터의 연산 - 내적과 외적

[3D수학] 벡터의 내적

백터의 외적

백터 값이 나온다.

3차원 좌표평면에서만 정의하는 개념이다.

크기와 방향을 가진다.

외적의 크기 : 두 백터를 변으로 하는 평행사변형의 넓이다.

외적의 방향 : 두 백터와 동시에 수직인 방향을 가리킨다.

외적의 특징

단위 백터끼리 외적하면 단위 백터가 나온다!

단위 백터끼리 외적하면 단위 백터가 나온다!

중요하니까 두 번 강조했다.

백터 A와 백터 B의 외적을 구하는 방법.

• 벡터의 외적은 위와 같은 식으로 표현되는데 이것은 아래와 같이 행렬식을 이용해서 계산하면 추론할수 있다.

• 외적의 크기 : 백터 A의 크기 백터 B의 크기 사인세타
• 외적의 방향 : 오른손 법칙을 이용, 수식의 왼쪽에 해당하는 백터를 손으로 가리키고 말았을 때 오른쪽에 해당하는 백터를 가리킬 때 엄지가 가리키는 방향이 된다.

https://www.youtube.com/watch?v=3GsBaTqxcjM&list=PLxz77rwoJPpXjltDYVC7KHqXEp-ejZaCJ&index=4

Vectors | Chapter 1, Essence of linear algebra

---

코드 (벡터 구조체, 벡터 연산 유틸 함수)

다시 한 번, 기본적인 구조나 함수들은 다음 실습 자료를 기반으로 진행했음을 밝힌다.

#ifndef STRUCTURES_H
# define STRUCTURES_H

typedef struct s_vec3 t_vec3; // 백터를 의미한다.
typedef struct s_vec3 t_point3; //  3차원 좌표계 위의 특정 한 점을 의미한다.
typedef struct s_vec3 t_color3; // RGB를 의미한다. x = R, y = G, z = B가 된다. 범위가 0~1 이므로 255.999 를 곱해서 사용한다.

struct s_vec3
{
    double x;
    double y;
    double z;
};
#endif

s_vec3라는 구조체로 백터, 좌표, 색깔을 전부 표현한다.

t_vec3, t_point3, t_color3 모두 같은 구조체를 사용하지만 의미하는 값이 다르다.

• t_vec3 - 벡터 그 자체. 가지고 있는 값은 원점(0, 0, 0)에서 출발하였을 때 종점이 가리키고 있는 좌표이다. 실사용에서 원점은 상황에 따라 이동될 수도 있다.
• t_point3 - 3차원 좌표계 위의 좌표. 특정한 지점을 의미한다.
• t_color3 - 픽셀이 가지게 될 색, RGB를 의미한다. x - R, y - G, z - B가 된다. 최대 범위는 0 ~ 255.

#include "utils.h"

//벡터3 생성자
t_vec3      vec3(double x, double y, double z)
{
    t_vec3 vec;

    vec.x = x;
    vec.y = y;
    vec.z = z;
    return (vec);
}

//포인트3 생성자
t_point3    point3(double x, double y, double z)
{
    t_point3 point;

    point.x = x;
    point.y = y;
    point.z = z;
    return (point);
}

//색상3 생성자
t_point3    color3(double r, double g, double b)
{
    t_color3 color;

    color.x = r;
    color.y = g;
    color.z = b;
    return (color);
}

// 벡터 값 설정
void        vset(t_vec3 *vec, double x, double y, double z)
{
    vec->x = x;
    vec->y = y;
    vec->z = z;
}

// 벡터 길이 제곱
double      vlength2(t_vec3 vec)
{
    return (vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
}

// 벡터의 길이, x^2 + y^2 + z^2의 제곱근
double      vlength(t_vec3 vec)
{
    return (sqrt(vlength2(vec)));
}

// 벡터합, x끼리, y끼리, z끼리 더한다.
t_vec3      vplus(t_vec3 vec, t_vec3 vec2)
{
    vec.x += vec2.x;
    vec.y += vec2.y;
    vec.z += vec2.z;
    return (vec);
}

// 벡터합2
t_vec3      vplus_(t_vec3 vec, double x, double y, double z)
{
    vec.x += x;
    vec.y += y;
    vec.z += z;
    return (vec);
}

// 벡터차, x끼리, y끼리, z끼리 뺀다.
t_vec3      vminus(t_vec3 vec, t_vec3 vec2)
{
    vec.x -= vec2.x;
    vec.y -= vec2.y;
    vec.z -= vec2.z;
    return (vec);
}

t_vec3      vminus_(t_vec3 vec, double x, double y, double z)
{
    vec.x -= x;
    vec.y -= y;
    vec.z -= z;
    return (vec);
}

t_vec3      vminus_self(t_vec3 vec)
{
    vec.x = -vec.x;
    vec.y = -vec.y;
    vec.z = -vec.z;
    return (vec);
}

// (단위)벡터 * 스칼라, 곱연산.
t_vec3      vmult(t_vec3 vec, double t)
{
    vec.x *= t;
    vec.y *= t;
    vec.z *= t;
    return (vec);
}

// 벡터 축 값끼리 곱연산
t_vec3      vmult_(t_vec3 vec, t_vec3 vec2)
{
    vec.x *= vec2.x;
    vec.y *= vec2.y;
    vec.z *= vec2.z;
    return (vec);
}

// 벡터 스칼라 나누기
t_vec3      vdivide(t_vec3 vec, double t)
{
    vec.x *= 1 / t;
    vec.y *= 1 / t;
    vec.z *= 1 / t;

    return vec;
}

// 벡터 내적
double      vdot(t_vec3 vec, t_vec3 vec2)
{
    return (vec.x * vec2.x + vec.y * vec2.y + vec.z * vec2.z);
}

// 벡터 외적
t_vec3      vcross(t_vec3 vec, t_vec3 vec2)
{
    t_vec3 new;

    new.x = vec.y * vec2.z - vec.z * vec2.y;
    new.y = vec.z * vec2.x - vec.x * vec2.z;
    new.z = vec.x * vec2.y - vec.y * vec2.x;
    return (new);
}

// 단위 벡터
t_vec3      vunit(t_vec3 vec)
{
    double len;
    
    len = vlength(vec);
    if (len == 0)
    {
        printf("Error\n:Devider is 0");
        exit(0);
    }
    vec.x /= len;
    vec.y /= len;
    vec.z /= len;
    return (vec);
}

// 두 벡터의 원소를 비교하여 작은 값들만 반환
t_vec3  vmin(t_vec3 vec1, t_vec3 vec2)
{
    if (vec1.x > vec2.x)
        vec1.x = vec2.x;
    if (vec1.y > vec2.y)
        vec1.y = vec2.y;
    if (vec1.z > vec2.z)
        vec1.z = vec2.z;
    return (vec1);
}

내적, 외적, 단위 백터를 구하는 유틸 함수들이다.

참고 자료

mini_raytracing_in_c/02.vector.md at main · GaepoMorningEagles/mini_raytracing_in_c

(2) 벡터에 대한 이해!