실습과 동일한 오른손 좌표계를 이용해서 3차원을 그릴 것이다. 엄지가 x축, 검지가 y축, 중지가 z축이 되어서 아래 사진처럼 나가는 방향이라고 우리는 정의하고 사용할 것이다. 오른손 좌표계를 default처럼 대부분 쓰고 있는 것 같다.
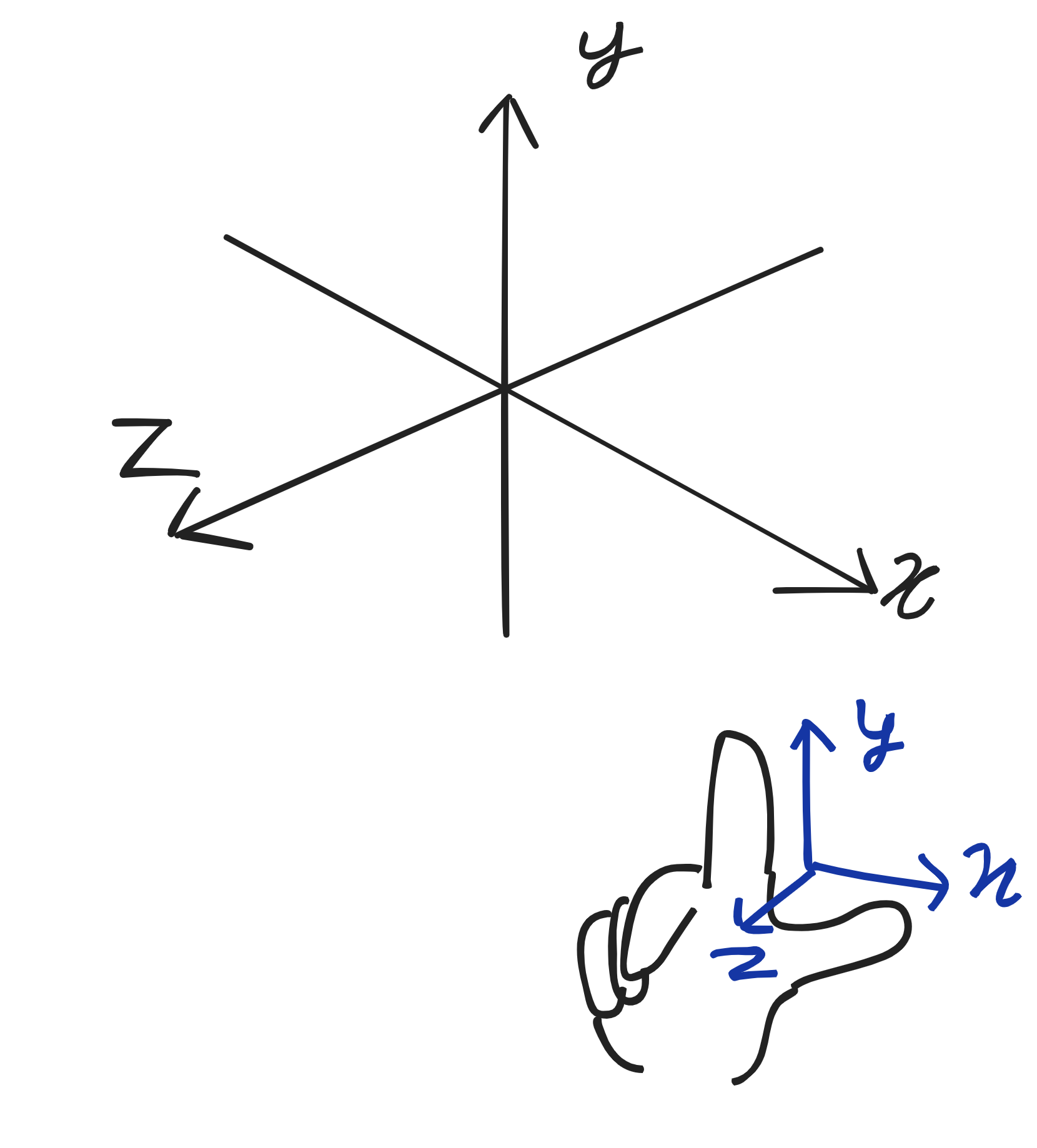
좌표계란 3차원 상에서 좌표의 각 축(x, y, z)에 대한 기준을 말하는 것으로, 공간 상의 모든 물체를 해당 좌표계를 기준으로 배치할 수 있게 된다.
개요
실습 자료와 실제 멘덴토리 상에서의 차이점이 생겼다.
실습 자료에서는 카메라를 구현할 때 가로, 세로가 가변적으로 들어갈 수 있다고 가정하여 종횡비를 고려한 처리를 진행하고 카메라의 원점이나 벡터도 고려하지 않았다.
그러나 실제 과제에서 화면(window)의 크기를 지정하라는 문구는 없었고 카메라의 원점이나 벡터도 고려해주어야 하기 때문에 실습 자료의 소스 코드와 비교하면서 멘덴토리에 맞게끔 코드를 수정해볼 것이다.
수정 전 코드(실습 소스 코드)
main.c
#include <stdio.h>
#include "structures.h"
#include "utils.h"
#include "print.h"
#include "scene.h"
#include "trace.h"
#include "mlx.h"
typedef struct s_data
{
void *img;
char *addr;
int bits_per_pixel;
int line_length;
int endian;
} t_data;
typedef struct s_vars {
void *mlx;
void *win;
t_data image;
} t_vars;
int create_trgb(int t, int r, int g, int b)
{
return (t << 24 | r << 16 | g << 8 | b);
}
void my_mlx_pixel_put(t_data *data, int x, int y, int color)
{
char *dst;
dst = data->addr + (y * data->line_length + x * (data->bits_per_pixel / 8));
*(unsigned int*)dst = color;
}
// esc key press event
int key_hook(int keycode, t_vars *vars)
{
if(keycode == 53)
{
mlx_destroy_window(vars->mlx, vars->win);
exit(0);
}
return (0);
}
int main(void)
{
int i;
int j;
double u;
double v;
t_color3 pixel_color;
t_canvas canv;
t_camera cam;
t_ray ray;
canv = canvas(600, 300);
cam = camera(&canv, point3(0, 0, 0));
t_vars vars;
t_data image;
vars.mlx = mlx_init();
vars.win = mlx_new_window(vars.mlx, canv.width, canv.height, "Hello miniRT!");
image.img = mlx_new_image(vars.mlx, canv.width, canv.height); // 이미지 객체 생성
image.addr = mlx_get_data_addr(image.img, &image.bits_per_pixel, &image.line_length, &image.endian); // 이미지 주소 할당
printf("P3\n%d %d\n255\n", canv.width, canv.height);
j = canv.height - 1;
while (j >= 0)
{
i = 0;
while (i < canv.width)
{
u = (double)i / (canv.width - 1);
v = (double)j / (canv.height - 1);
ray = ray_primary(&cam, u, v);
pixel_color = ray_color(&ray);
write_color(pixel_color);
my_mlx_pixel_put(&image, i, canv.height - 1 - j, create_trgb(0, pixel_color.x * 255.999, pixel_color.y * 255.999, pixel_color.z * 255.999));
++i;
}
--j;
}
mlx_put_image_to_window(vars.mlx, vars.win, image.img, 0, 0);
mlx_key_hook(vars.win, key_hook, &vars);
mlx_loop(vars.mlx);
return (0);
}기존 실습 자료의 소스 코드에 mlx 상에서 윈도우를 띄우도록 코드를 임의로 추가해 준 것 말고는 실습 자료의 코드와 동일하다.
scene.c
#include "scene.h"
t_camera camera(t_canvas *canvas, t_point3 orig)
{
t_camera cam;
double focal_len;
double viewport_height;
viewport_height = 2.0;
focal_len = 1.0;
cam.orig = orig;
cam.viewport_h = viewport_height;
cam.viewport_w = viewport_height * canvas->aspect_ratio;
cam.focal_len = focal_len;
cam.horizontal = vec3(cam.viewport_w, 0, 0);
cam.vertical = vec3(0, cam.viewport_h, 0);
// 왼쪽 아래 코너점 좌표, origin - horizontal / 2 - vertical / 2 - vec3(0,0,focal_length)
cam.left_bottom = vminus(vminus(vminus(cam.orig, vdivide(cam.horizontal, 2)),
vdivide(cam.vertical, 2)), vec3(0, 0, focal_len));
return (cam);
}레이를 쏘는 벡터 구하기
main.c
while (j >= 0)
{
i = 0;
while (i < canv.width)
{
u = (double)i / (canv.width - 1);
v = (double)j / (canv.height - 1);
ray = ray_primary(&cam, u, v);
pixel_color = ray_color(&ray);
write_color(pixel_color);
my_mlx_pixel_put(&image, i, canv.height - 1 - j, create_trgb(0, pixel_color.x * 255.999, pixel_color.y * 255.999, pixel_color.z * 255.999));
++i;
}
--j;
}앞선 정리에서 뷰포트의 픽셀 하나하나를 2차원 배열의 요소로 표현해 줄 수 있다고 말했었다. 실습 자료의 소스 코드에서도 지정해준 뷰포트(캔버스)의 높이, 넓이만큼 이중 while문을 돌아가며 mlx 이미지에 값을 집어넣었다.
ray.c
t_ray ray_primary(t_camera *cam, double u, double v)
{
t_ray ray;
ray.orig = cam->orig;
// left_bottom + u * horizontal + v * vertical - origin 의 단위 벡터.
ray.dir = vunit(vminus(vplus(vplus(cam->left_bottom, vmult(cam->horizontal, u)), vmult(cam->vertical, v)), cam->orig));
return (ray);
}이중 while문을 돌며 i, j에 따라 카메라에서 뷰포트의 어느 픽셀에 대해 광선을 쏠 것인지, 그 광선의 방향 벡터는 무엇인지가 정해진다. 이는 뷰포트의 제일 왼쪽 아래에 있는 픽셀(cam->left_bottom)을 기준으로 정해진다.
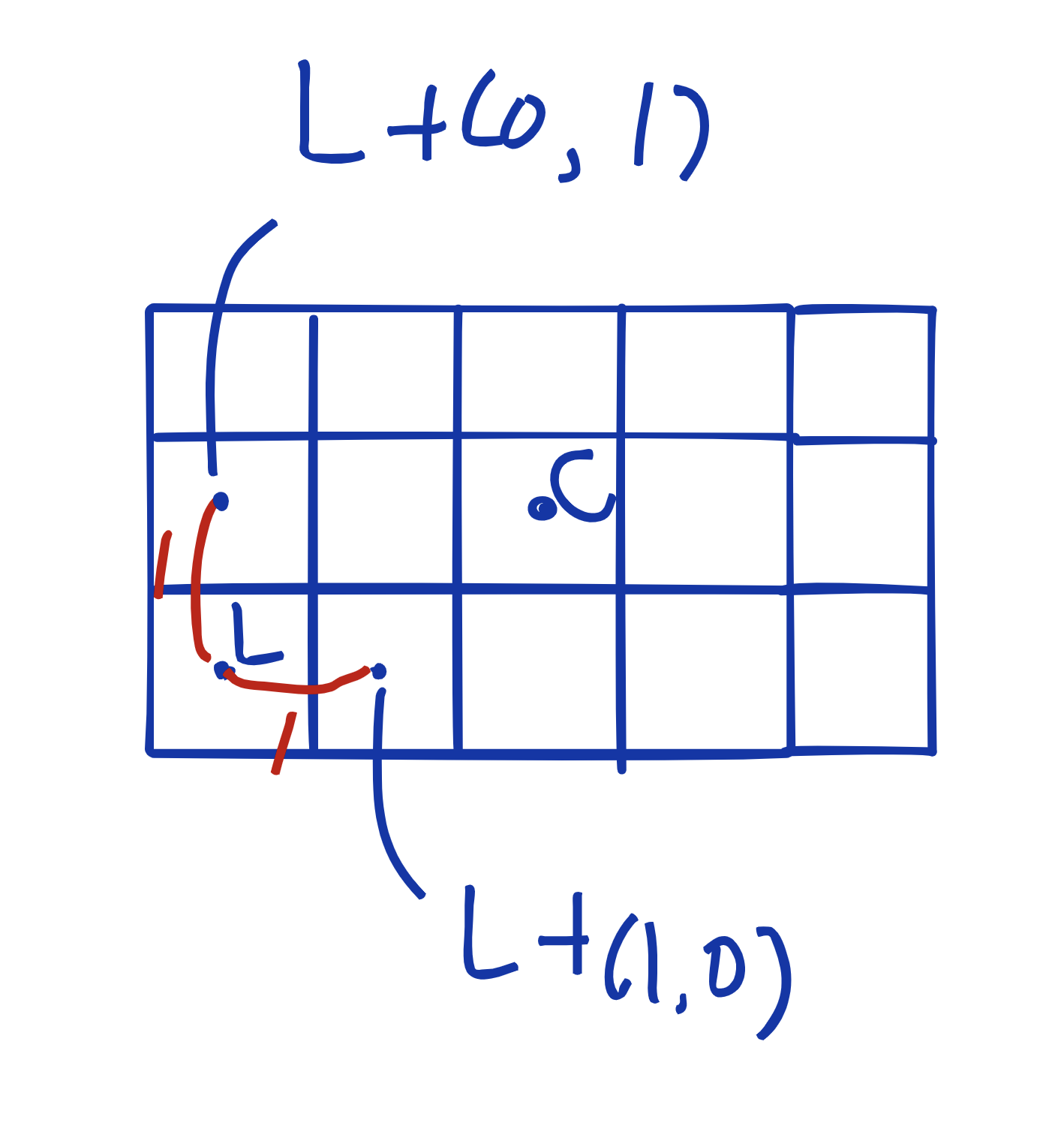
각 픽셀 간의 간격을 1로 놓고 보았을 때, 가장 왼쪽 아래의 픽셀의 중심 좌표를 알게 된다면 다른 모든 픽셀들을 x만큼 y만큼 더하는 것으로 표현할 수 있게 되는 것이다. 그렇다면 왼쪽 아래 픽셀의 좌표는 어떻게 구할 수 있을까?
뷰포트 왼쪽 아래의 픽셀(의 중심) 좌표 구하기
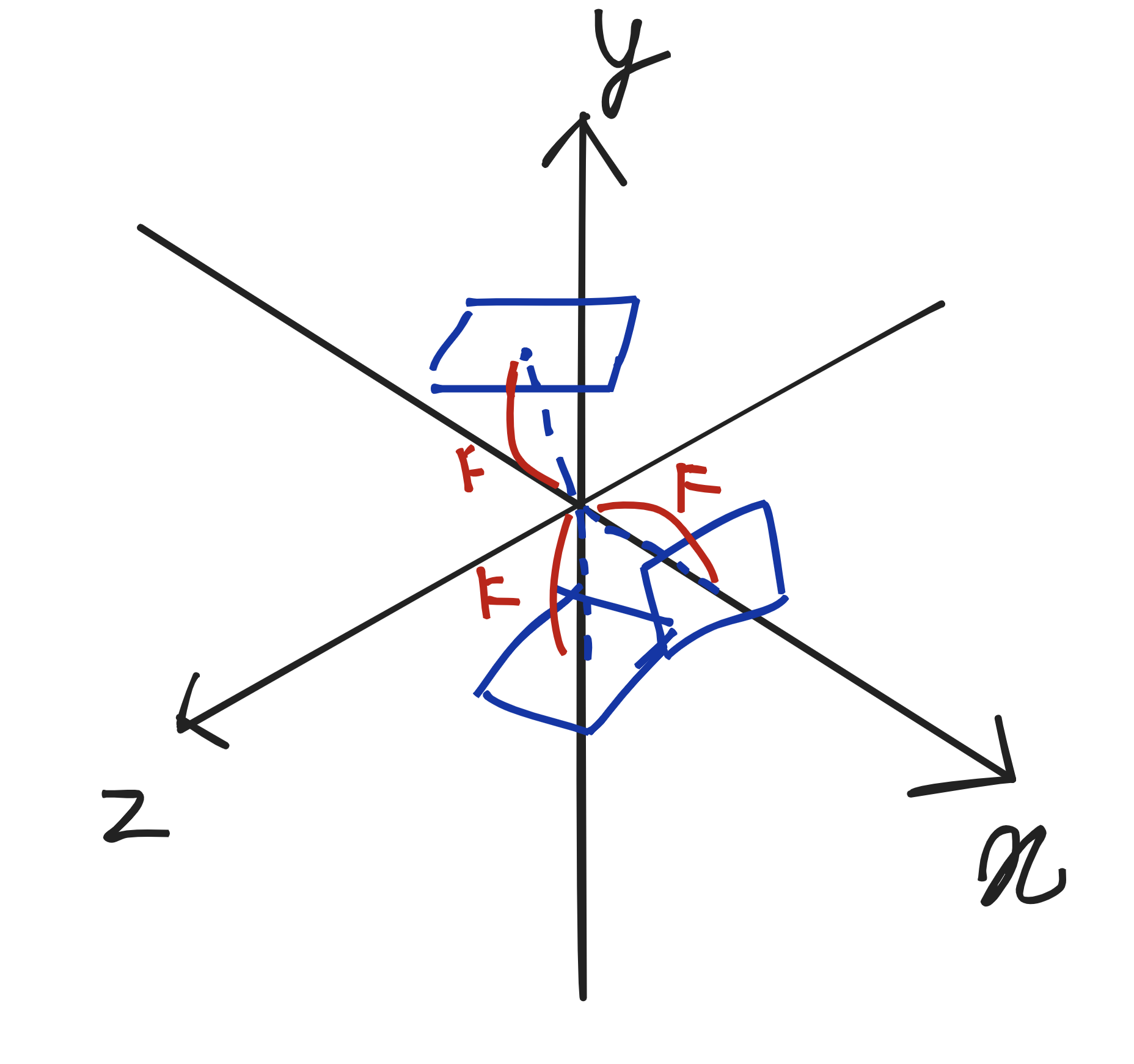
카메라의 벡터가 있을 때, 뷰포트는 카메라와 focal_len인 F만큼 떨어진 위치에 카메라의 벡터를 뷰포트(켄버스)의 정중앙으로 해서 떠있는 형태가 된다.
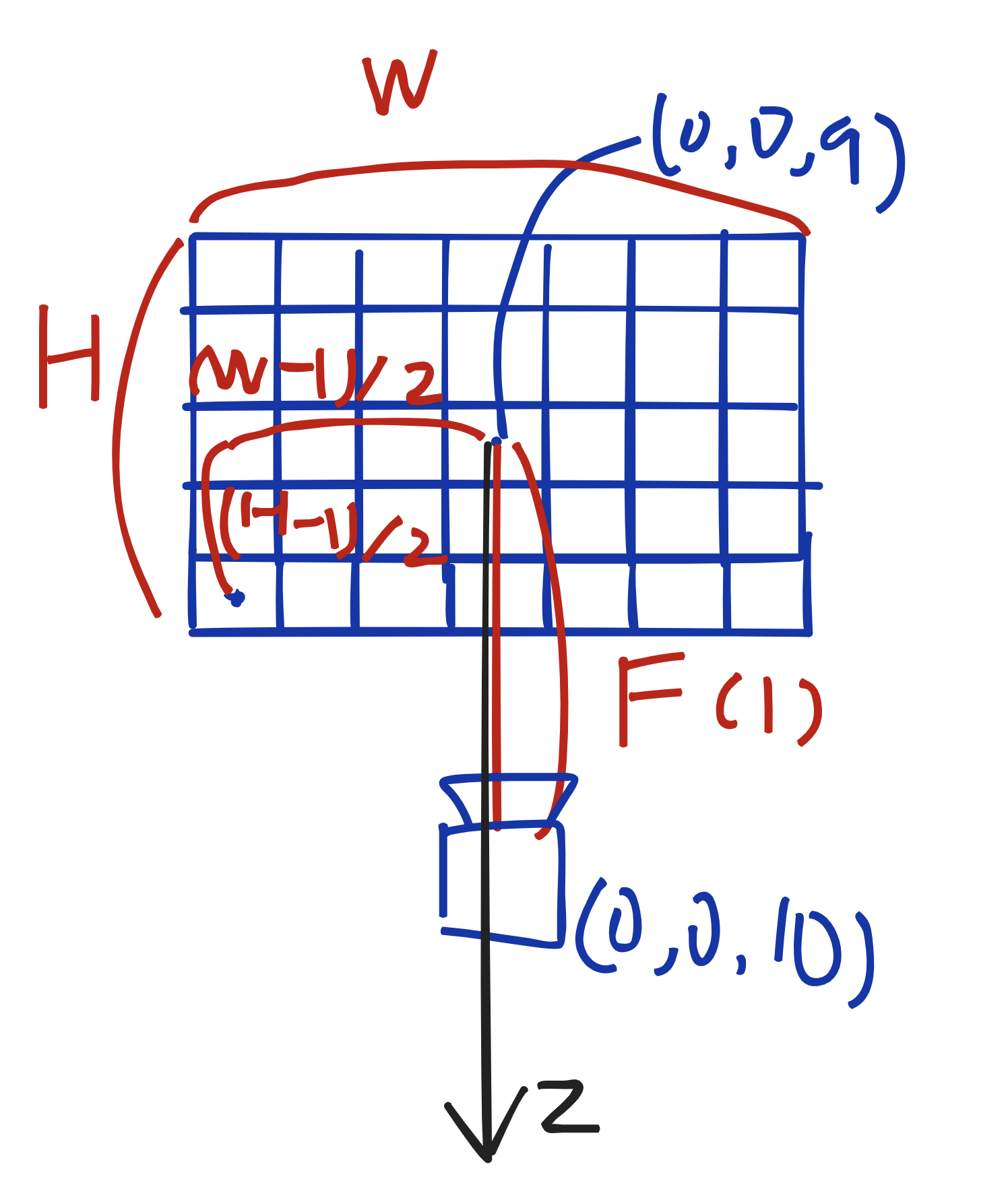
카메라의 벡터가 (0, 0, -1)이라고 할 때, 카메라와 뷰포트는 다음과 같아진다.
인자로 들어오게 되는 정보는 다음과 같다.
- 카메라가 위치한 좌표
- 카메라의 방향 벡터(바라보는 방향)
- 뷰포트(캔버스)의 넓이와 높이
- 뷰포트의 화각
이를 통해 뷰포트의 왼쪽 아래 픽셀의 좌표를 구해야 한다. 식은 다음과 같다.
뷰포트의 중앙 지점 - (뷰포트의 넓이 - 1) / 2 - (뷰포트의 높이 - 1) / 2 = 뷰포트의 왼쪽 아래 픽셀
이를 알려면 두 가지 정보를 알아야 한다.
- 뷰포트의 중앙점을 알아야 한다.
- 카메라의 좌표에서 카메라와 뷰포트까지의 거리를 빼주면 곧 뷰포트의 중앙점이 된다.
- 위의 그림에서는 편의상 카메라와 뷰포트까지의 거리를 1이라고 넣어두었지만 실제로는 화각에 따라 거리가 달라지게 될 것이다.
- 카메라의 방향 벡터와 수직하는 오른쪽 벡터, 위쪽 벡터를 구해야 한다.
- 위에서는 단순하게 뷰포트의 넓이, 높이를 빼주면 된다고 말했지만 2차원 상의 공간으로 단순하게 말한 것이었기 때문이다. 벡터가 3차원적일 경우 1씩 빼주었을 때 픽셀 역시 정확히 한 칸 움직일 것이라고 확신할 수 없다.
수정 작업
그러나 실습 자료의 소스 코드에서는 카메라의 방향 벡터, 화각에 대한 것을 고려하지 않았다.
위의 실습 자료를 멘덴토리에 맞게 바꾸기 위해 다음 작업을 진행해야 한다.
- 인자로 파일 받아서 파싱하기
- canvas 구조체 제거하기
- 고정된 window를 사용할 것이기에 종횡비를 설정할 필요가 없다.
- FOV 값 적용시키기
- 카메라의 방향 벡터에 대한 값 적용하기
카메라 벡터에 따른 우측 벡터 위쪽 벡터 구하기

struct s_camera
{
t_point3 origin; // 카메라 원점(위치)
t_vec3 dir; // 카메라 벡터
t_vec3 right_normal; // 카메라 벡터가 평면이 아닐 때의 left_bottom을 구하기 위해
t_vec3 up_normal; // 카메라 벡터가 평면이 아닐 때의 left_bottom을 구하기 위해
t_point3 left_bottom; // 왼쪽 아래 코너점
double fov; // 화각
double focal_len; // 화각에 따라 카메라와 viewport와의 거리가 달라진다.
// 제거
// double viewport_h; // 뷰포트 세로길이
// double viewport_w; // 뷰포트 가로길이
// t_vec3 horizontal; // 수평길이 벡터
// t_vec3 vertical; // 수직길이 벡터
};카메라 구조체를 다음처럼 수정해주었다. 인자로 들어오는 카메라 벡터와 해당 카메라 벡터의 왼쪽(수평), 위쪽(수직) 벡터를 구해주어야 한다. 역시 인자로 들어오는 화각에 대한 값도 담겨야 한다.
scene.c
#include "scene.h"
#define WIDTH 600
#define HEIGHT 300
float get_tan(float degree)
{
static const float radian = M_PI / 180;
return (tan(degree * radian));
}
t_camera camera(t_point3 orig, t_vec3 dir)
{
t_camera cam;
t_vec3 vec_y;
t_vec3 vec_z;
t_vec3 temp;
vec_y = vec3(0.0, 1.0, 0.0);
vec_z = vec3(0.0, 0.0, -1.0);
cam.orig = orig;
cam.dir = dir;
cam.fov = 90;
if (vlength(vcross(vec_y, cam.dir)))
cam.right_normal = vunit(vcross(cam.dir, vec_y));
else
cam.right_normal = vunit(vcross(cam.dir, vec_z));
cam.up_normal = vunit(vcross(cam.right_normal, cam.dir));
cam.focal_len = (float)WIDTH / 2 / get_tan(cam.fov / 2);
temp = vplus(cam.orig, vmult(cam.dir, cam.focal_len));
temp = vminus(temp, vmult(cam.right_normal, -(float)(WIDTH - 1)/ 2));
temp = vminus(temp, vmult(cam.up_normal, -(float)(HEIGHT - 1)/ 2));
cam.left_bottom = temp;
print_vec(cam.right_normal);
print_vec(cam.up_normal);
print_vec(cam.left_bottom);
return (cam);
}기존의 코드는 하드 코딩된 focal_len, viewport_height와 종횡비에 따라 left_bottom 좌표를 구했다.
- 캔버스와 뷰포트가 동일하다고 보면 종횡비를 구할 필요는 없다.
- 카메라 벡터에 따라 수평 벡터, 수직 벡터가 변해야 한다.
- 카메라 벡터의 머리 위 수직으로 뻗어나가는 벡터인 vec_y와 외적을 해주어서 오른쪽으로 뻗는 벡터를 구한다. 이 때 카메라의 벡터도 y축에 대한 값만 가지고 있을 때 외적의 결과가 0이 나오기 때문에 vec_z와 외적을 진행한 결과를 표준화하면 right_normal이 된다.
- right_normal과 카메라의 방향 벡터를 외적하고 표준화한다면 right_up이 나온다.
외적 순서를 바꾸면 안된다!
카메라 FOV 값 구하기
위에서 같이 넘어갔지만, 각도가 얼마냐에 따라 카메라와 뷰포트 사이의 거리가 달라지게 된다. 그것을 구하는 공식이 cam.focal_len = (float)WIDTH / 2 / get_tan(cam.fov / 2); 가 된다.
아직 인자로 받는 것은 아니기에 하드 코딩으로 값을 넣어주었다.
광선 벡터 구하기
t_ray ray_primary(t_camera *cam, double u, double v)
{
t_ray ray;
t_vec3 horizontal;
t_vec3 vertical;
t_point3 viewport_point;
ray.orig = cam->orig; // 0, 0, 0
horizontal = vmult(cam->right_normal, u);
vertical = vmult(cam->up_normal, v);
viewport_point = vplus(cam->left_bottom, horizontal);
viewport_point = vplus(viewport_point, vertical);
ray.dir = vunit(vminus(viewport_point, ray.orig));
return (ray);
}left_bottom 값, 카메라 벡터의 오른쪽인 벡터, 카메라 벡터의 위쪽인 벡터 값을 우리는 알고 있다.
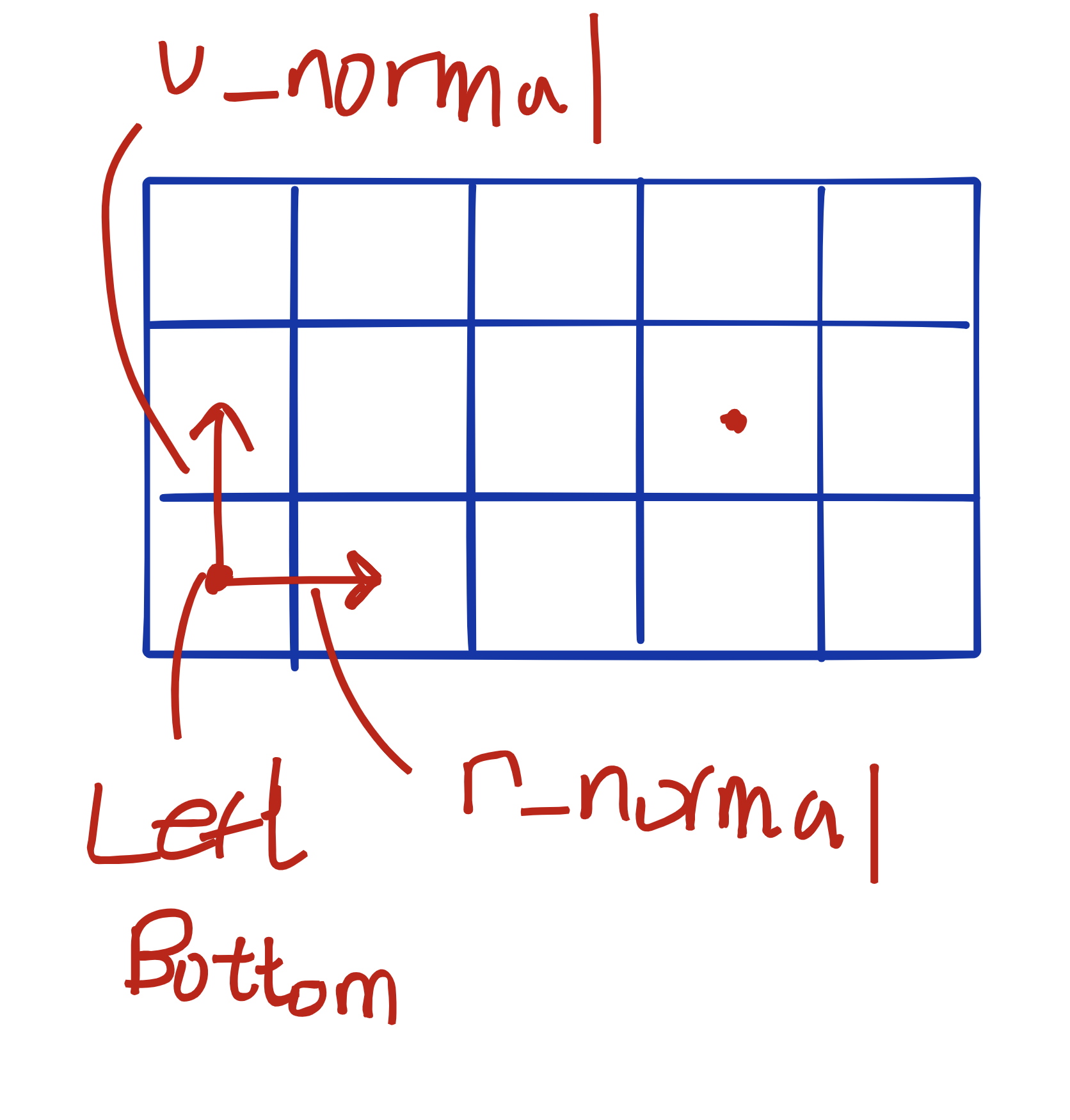
viewport의 어느 픽셀이든 while 문의 u, v(x축인 j, y축인 i) 값만 알고 있다면 left_bottom에서 cam->right_normal u, cam→up_normal v 만큼 곱해서 나온 벡터를 더해주기만 하면 해당 픽셀의 위치가 나오게 된다.
픽셀의 위치를 구하면 해당 픽셀의 좌표에 카메라 원점 좌표를 빼고 나온 값을 표준화해주기만 하면 해당 픽셀에 대한 광선을 구할 수 있다.
광선 발사 로직
static void raytracing(t_scene *scene, t_mlx *mlx)
{
int i; // x
int j; // y
t_color3 pixel_color;
j = HEIGHT - 1;
while (j >= 0)
{
i = 0;
while (i < WIDTH)
{
printf ("x : %d y : %d\n", i, j);
scene->ray = ray_primary(&scene->camera, i, j); // 광선의 방향 벡터가 정해진다.
print_vec(scene->ray.dir); // 확인을 위한 출력 코드.
pixel_color = ray_color(scene); // 광선을 발사하여 물체와 충돌 유무에 따라 색이 변한다.
my_mlx_pixel_put(mlx, i, HEIGHT - 1 - j, create_trgb(0, pixel_color.x, pixel_color.y, pixel_color.z));
// 위쪽에서부터 찍을 것이기에 높이에서 빼줌.
++i;
}
--j;
}
}넓이(x) 300, 높이(y) 150 뷰포트(캔버스) 기준.
실제 코드에서 x는 0 ~ 299, y는 0 ~ 149의 범위를 가지고 반복문을 돌아가며 뷰포트의 픽셀을 정하게 된다. 300 * 150로, 이 뷰포트는 총 45000번의 광선 발사를 통해 정해진 픽셀로 이루어져 있는 셈이다.
x : 191 y : 50
x : 0.189001, y : -0.111579, z : -0.975617
x : 192 y : 50
x : 0.193386, y : -0.111482, z : -0.974768
x : 193 y : 50
x : 0.197761, y : -0.111382, z : -0.973902
x : 194 y : 50
x : 0.202123, y : -0.111281, z : -0.973017
x : 195 y : 50
x : 0.206474, y : -0.111178, z : -0.972115
x : 196 y : 50
x : 0.210812, y : -0.111073, z : -0.971196
x : 197 y : 50
x : 0.215138, y : -0.110966, z : -0.970259
x : 198 y : 50
x : 0.219451, y : -0.110857, z : -0.969305
x : 199 y : 50
x : 0.223751, y : -0.110746, z : -0.968334
x : 200 y : 50
x : 0.228039, y : -0.110633, z : -0.967346
x : 201 y : 50
x : 0.232313, y : -0.110518, z : -0.966342
x : 202 y : 50
x : 0.236574, y : -0.110401, z : -0.965321
x : 203 y : 50
x : 0.240821, y : -0.110282, z : -0.964284
x : 204 y : 50
x : 0.245054, y : -0.110162, z : -0.963230
x : 205 y : 50
x : 0.249274, y : -0.110040, z : -0.962161
x : 206 y : 50
x : 0.253479, y : -0.109916, z : -0.961076
x : 207 y : 50
x : 0.257670, y : -0.109790, z : -0.959975
x : 208 y : 50
x : 0.261846, y : -0.109662, z : -0.958859
x : 209 y : 50
x : 0.266008, y : -0.109533, z : -0.957728
x : 210 y : 50
x : 0.270155, y : -0.109402, z : -0.956581
x : 211 y : 50
x : 0.274287, y : -0.109269, z : -0.955420
x : 212 y : 50
x : 0.278404, y : -0.109134, z : -0.954244
x : 213 y : 50
x : 0.282505, y : -0.108998, z : -0.953053
x : 214 y : 50
x : 0.286591, y : -0.108860, z : -0.951848
x : 215 y : 50
x : 0.290662, y : -0.108721, z : -0.950629
x : 216 y : 50
x : 0.294717, y : -0.108580, z : -0.949396
x : 217 y : 50
x : 0.298755, y : -0.108437, z : -0.948149
x : 218 y : 50
x : 0.302778, y : -0.108293, z : -0.946889위의 로그는 실제 반복문을 돌아가면서 뷰포트의 x, y에 따른 광선의 방향 벡터를 구한 결과를 로그로 찍은 것이다.
참고 자료
(5) Raytracing One Weekend 식 이해하기! 2
mini_raytracing_in_c/03.ray_and_camera.md at main · GaepoMorningEagles/mini_raytracing_in_c
