[miniRT] #6 법선 구현

sham·2022년 3월 31일

42Seoul miniRT

[miniRT]

목록 보기

6/19

역시나 실습 자료를 기반으로 작성하였다.

레이를 쏜 백터 길이(t) 구하기

근의 공식을 이용해서 레이의 단위 백터와 구의 충돌 여부에 대해서 구할 수 있었다. 이제는 구와 레이의 정확한 교점을 구해서 명도를 조절해줄 것이다.

정확한 교점을 구한다는 것은 t에 대한 해를 구해서 충돌한 해당 광선이 출발 지점에서부터 얼마만큼의 거리인지를 구할 수 있다는 의미가 된다.

At^2 + Bt + C = 0

{-b \pm \sqrt{b^2 - 4ac} } \over {2a}

hit_sphere.c

#include "structures.h"
#include "utils.h"

//t_bool에서 double로 변환.
double      hit_sphere(t_sphere *sp, t_ray *ray)
{
    ...
    discriminant = b * b - 4 * a * c;

    /* * * * 수정 * * * */
    if (discriminant < 0) // 판별식이 0보다 작을 때 : 실근 없을 때,
        return (-1.0);
    else
        return ((-b - sqrt(discriminant)) / (2 * a)); // 두 근 중 작은 근
    /* * * * 수정 끝 * * * */
}

discriminant 는 근의 공식의 판별식만을 처리한 것이기에 음수일 경우에는 -1을 리턴하고 0 이상이면 해를 구하기 위한 나머지 처리를 진행한다.

여기서 리턴하는 값이 그토록 원했던 t, 광선을 쏜 백터의 스칼라에 대한 값이다.

법선 벡터(Normal Vector)

물체 표면과 빛의 상호작용을 계산하기 위해 법선을 이용할 것이다. 법선은 어떤 표면에 수직인 방향으로 뻗어나가는 벡터로, 광선과 구체가 부딪힌 지점에서 수직으로 뻗어나가는 벡터를 이용하면 구, 관성의 교점, 구의 중심을 나눠주면 정규화된 법선을 구할 수 있다. 어떻게?

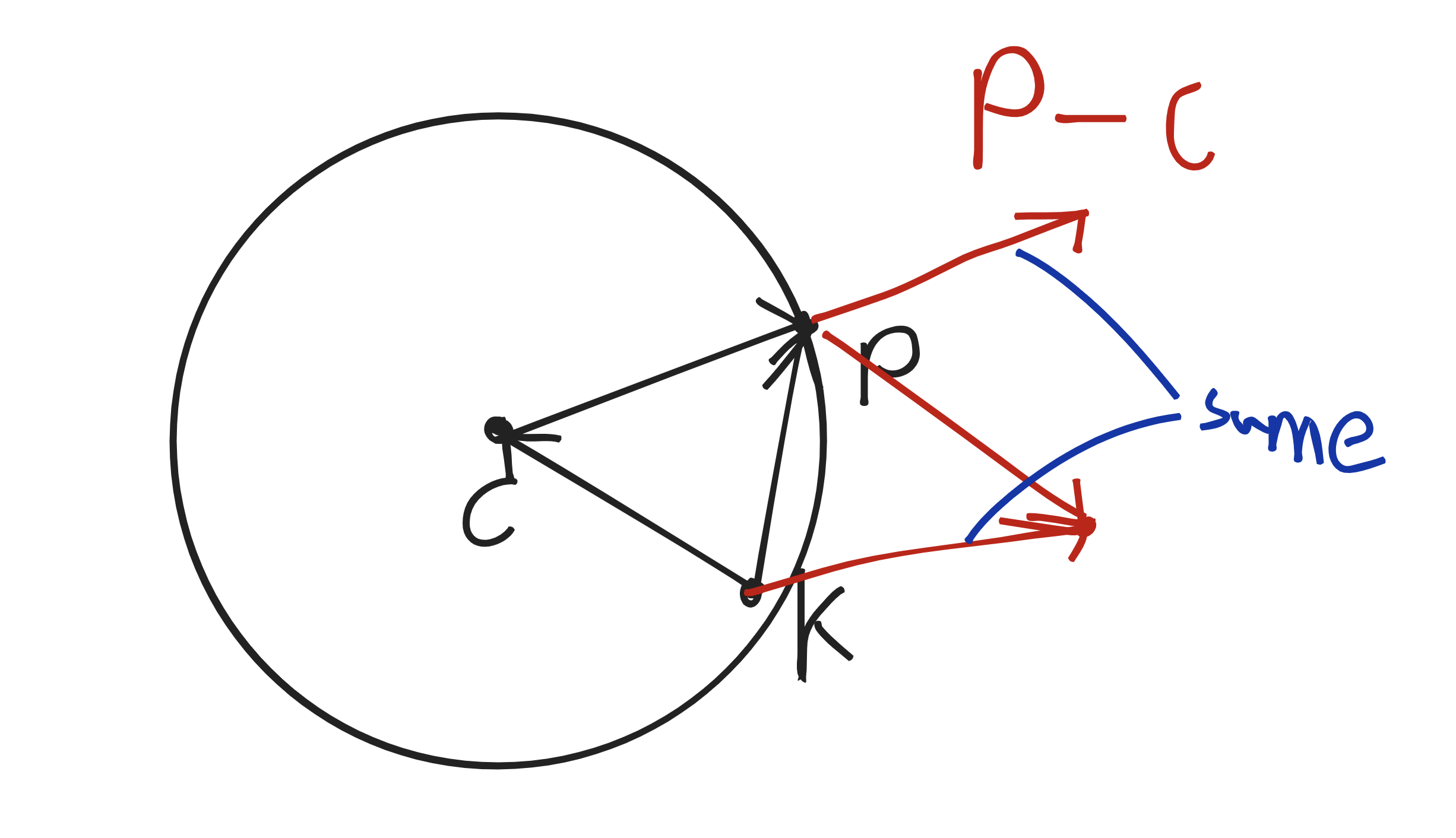
우리는 구와 광선의 교점, 구의 중심을 알고 있다. 교점에서 중심을 빼준 뒤 구의 반지름으로 나눠주면 정규화된 법선을 구할 수 있다.

위의 그림이 잘 이해가 가지 않는다면 직접 그려보자.

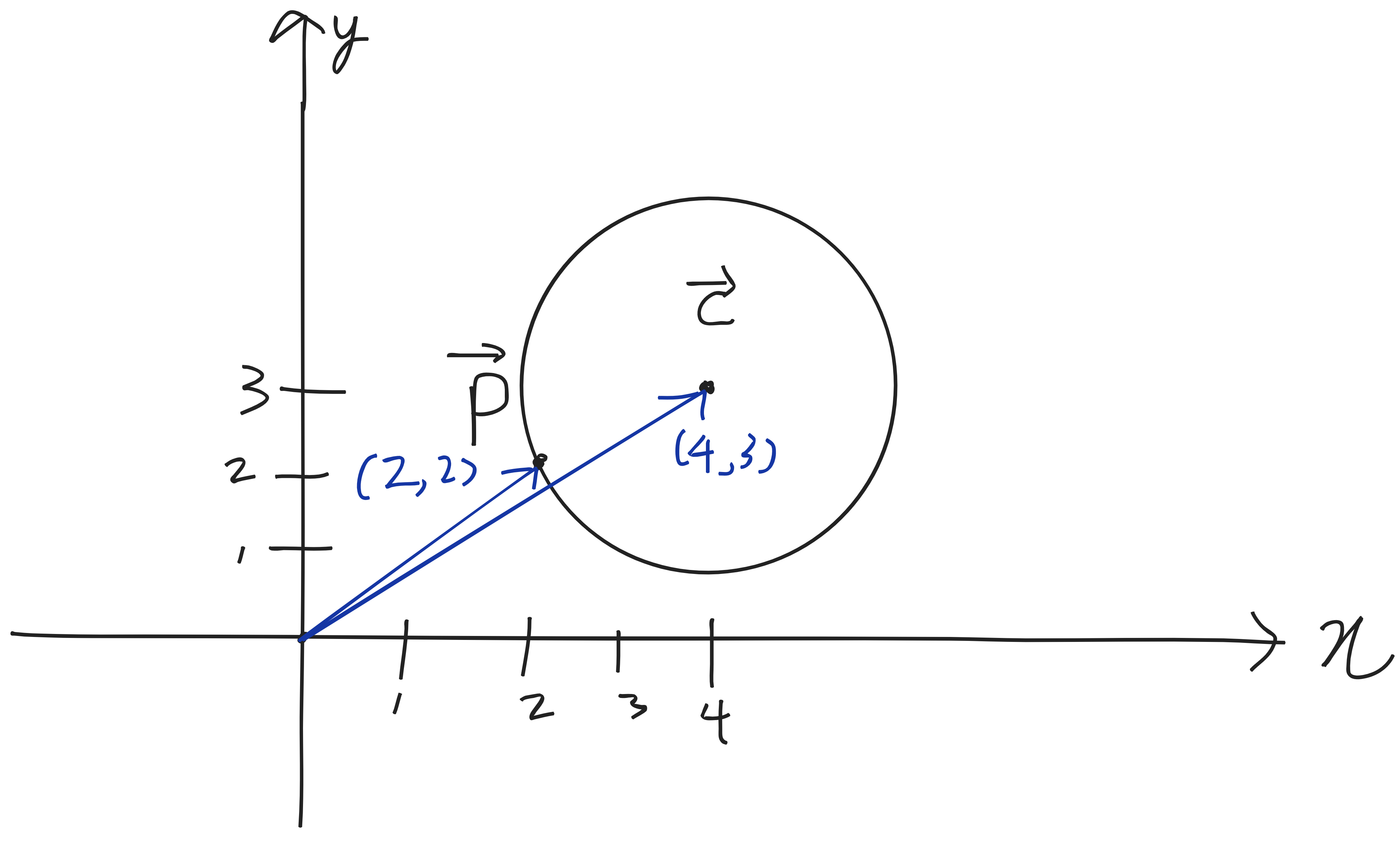
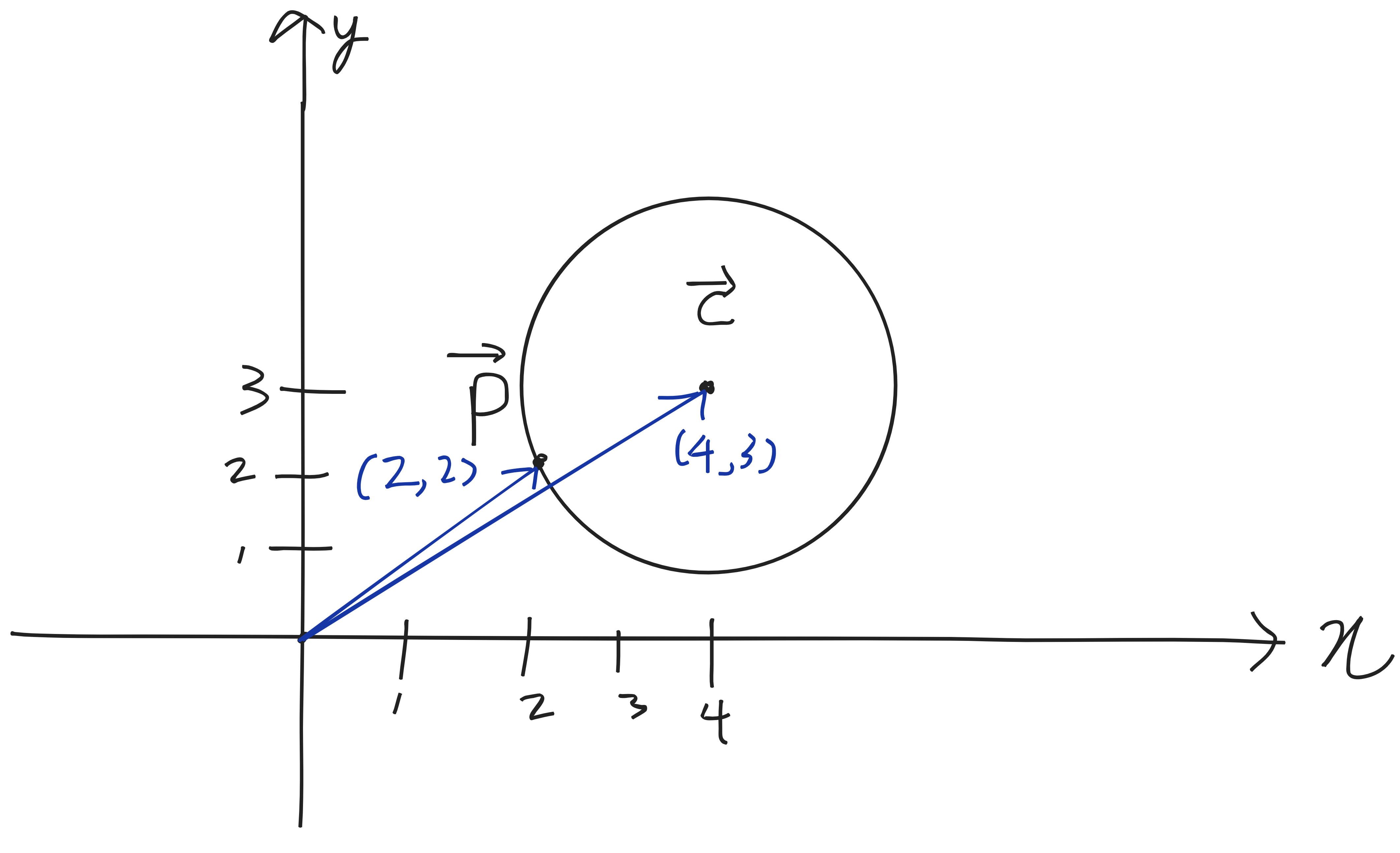
백터와 좌표

P와 C는 벡터이기도 하고, 3차원 상의 좌표이기도 하다. 서로 섞여서 사용하더라도 아무런 문제가 없다.

위 그림의 C, P를 가지고 2차원 좌표 평면 상에서 실험을 해보자.

백터로 보았을 때

백터는 방향과 크기를 가지고 있다. 풀어보면 원점 + 단위 벡터 * 길이(스칼라)인데, 수식으로 보면 다음과 같다.

P(t) = O + D\times t

위의 그림을 위의 수식처럼 대입시켜 보자. 원점에 대해 알고 있지만 단위 백터와 길이에 대해서는 우린 알지 못한다.

단위 벡터 구하기

단위 백터를 구하는 수식은 다음과 같다.

U = ({x\over\sqrt{x^2 + y^2}}, {y\over / \sqrt{x^2 + y^2}})

x, y에 대한 값을 알고 있으니 벡터 P와 벡터 C의 단위벡터를 직접 구해보자.

\vec P = ({2\over\sqrt{2^2 + 2^2}}, {2\over / \sqrt{2^2 + 2^2}}) = ({2\over\sqrt{8}}, {2\over \sqrt{8}})

\vec C = ({4\over\sqrt{4^2 + 3^2}}, {3\over / \sqrt{4^2 + 3^2}}) = ({4\over5}, {3\over 5})

길이 구하기

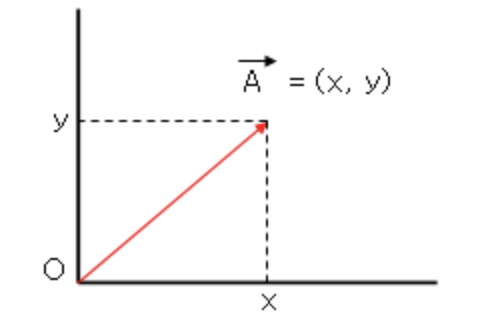
x, y 좌표를 알기에 우리는 피타고라스의 정리를 이용해서 삼각형의 빗면, 벡터의 길이를 구할 수 있다.

a = \sqrt{x^2 + y^2}

|A| = \sqrt{x^2 + y^2}

벡터 P와 벡터 C의 길이를 직접 구해보자.

|\vec P| = \sqrt{2^2 + 2^2} = \sqrt{8}

|\vec C| = \sqrt{4^2 + 3^2} = 5

증명

P(t) = O + D\times t

\vec P = O + D\times t = (0 ,0) + ({2\over\sqrt{8}}, {2\over \sqrt{8}}) \times \sqrt{8} = (2, 2)

\vec C = O + D\times t = (0 ,0) + ({4\over5}, {3\over 5}) \times 5 = (4, 3)

이로써 벡터와 좌표는 사실상 동일하다고 볼 수 있다는 것이 증명되었다.

굳이 증명하지 않아도 쉽게 알 수 있는 것이, 원점(0, 0, 0)에서 뻗어나가 결과적으로 닿는 벡터의 종점이 바로 좌표다. 백터, 좌표를 의미하는 구조체가 똑같은 구조를 가지는 것이 바로 이 때문이다.

법선 벡터 실제로 구해보기

위의 그림을 그대로 가져와서 실제로 좌표 위에서 법선 벡터를 구해보자.

벡터의 뺄셈

\overrightarrow{CP} = \vec{P} - \vec{C}

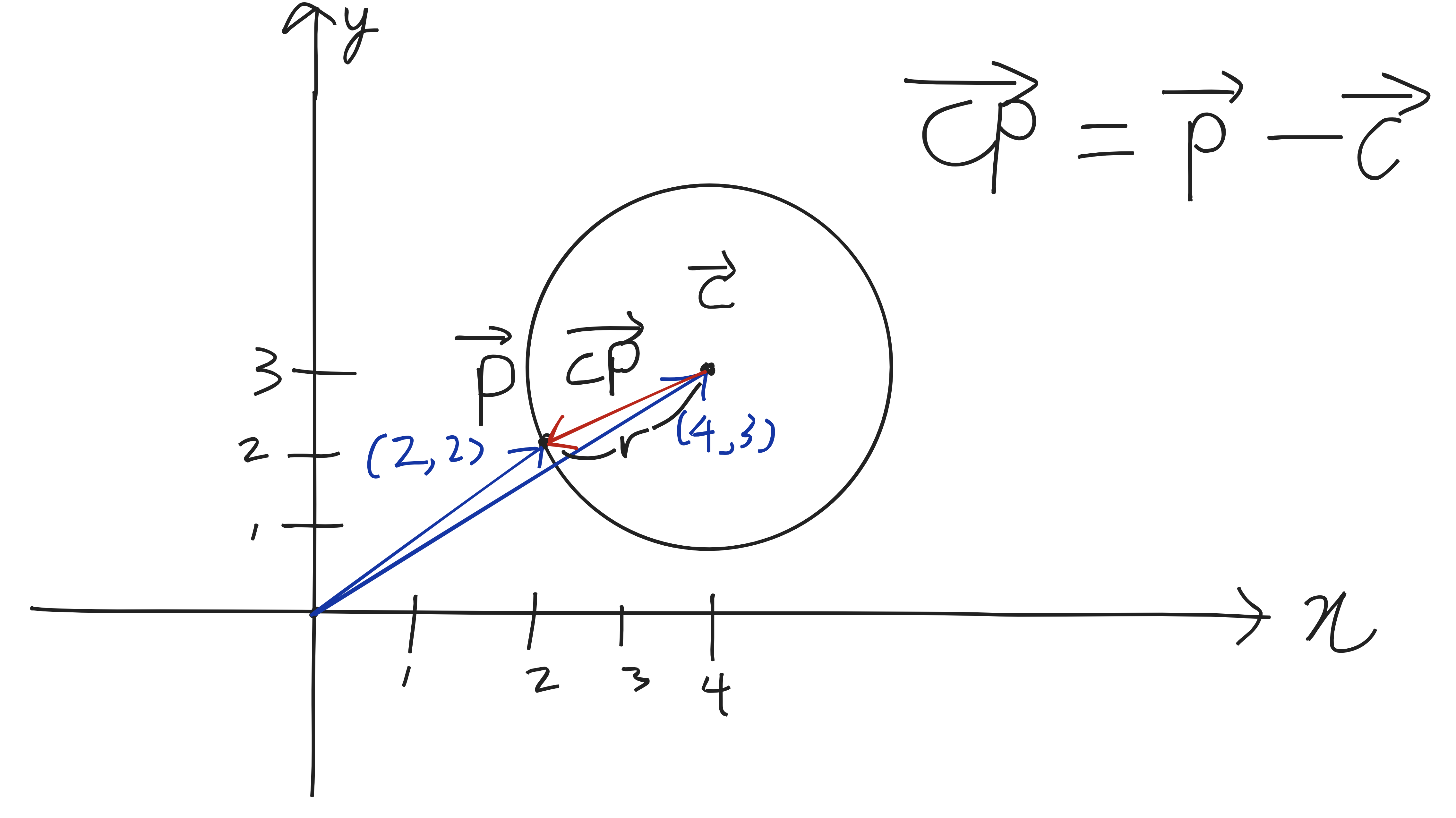
벡터 CP는 벡터 P - 벡터 C와도 같다. 어째서인가? 벡터의 방향과 크기가 같다면 위치에 상관하지 않고 동일하다고 판단하기 때문이다.

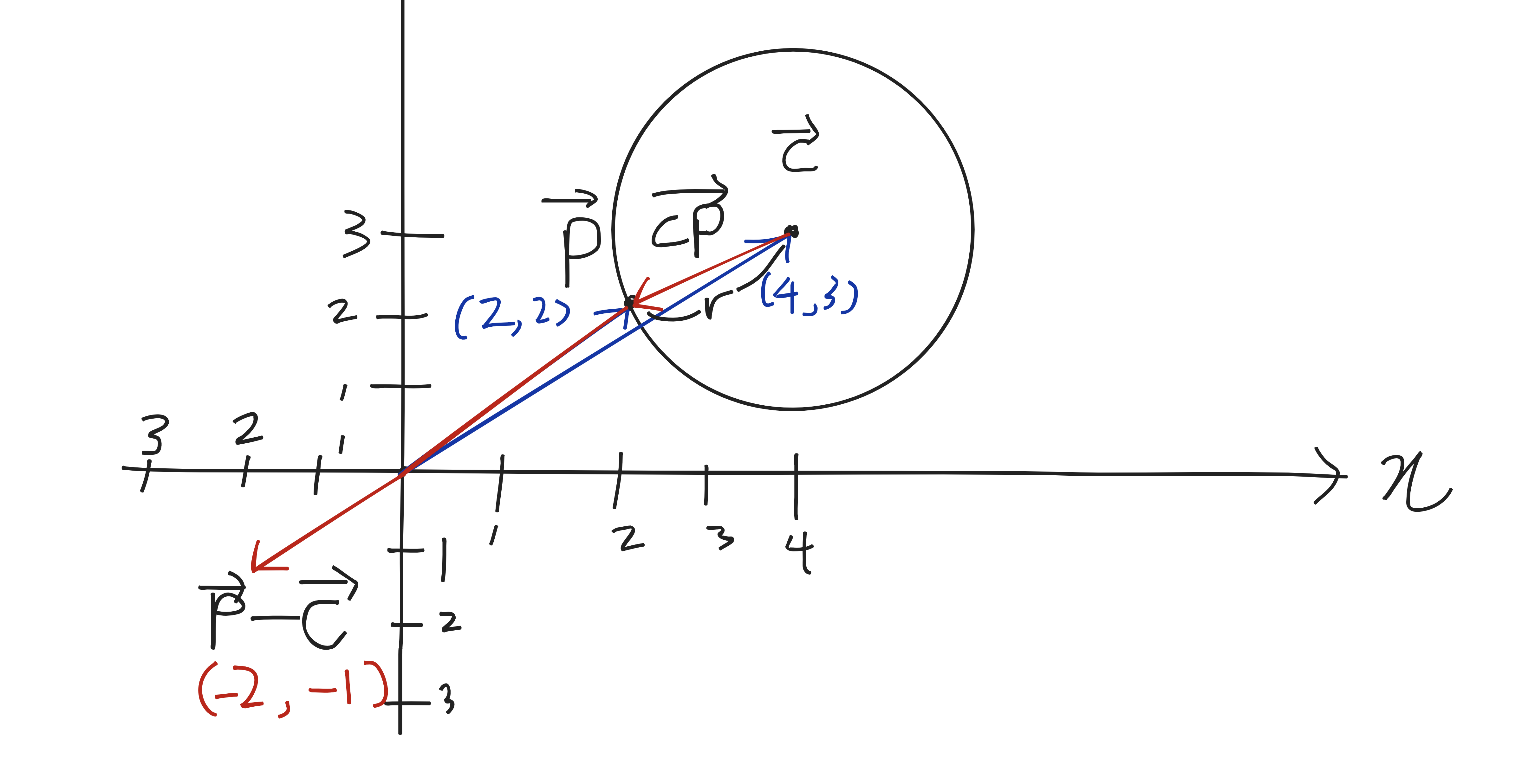
벡터의 뺄셈은 x끼리, y끼리 각 요소를 빼주는 것인데, 시각적으로 확인하고 싶다면 피연산자 벡터의 종점에서부터 연산자 벡터가 반대 방향으로 뻗어나가도 된다. 결과는 똑같다.

\vec{P} - \vec{C} = (\vec{P}.x - \vec{C}.x , \vec{P}.y - \vec{C}.y) = (-2, -1)

단위 벡터 구하기

법선 벡터를 구하는데 성공했지만, 아직 단위 벡터는 아니다.

단위 벡터를 구하는 수식에 법선 벡터의 값을 집어넣자.

U = ({-2\over\sqrt{-2^2 + -1^2}}, {-1\over / \sqrt{-2^2 + -1^2}}) = ({-2\over\sqrt{5}}, {-1\over \sqrt{5}})

분모의 값은 반지름의 값과도 같다. -2^2 * -1^2의 제곱근인 √5가 바로 (-2, -1) 벡터의 길이이자 반지름이기 때문이다.

이 길고 긴 과정을 끝내고서야 우리는 최종적으로 광선이 물체와 부딪혔을 때의 교점과 수직이 되는 벡터, 동시에 길이를 1로 보는 단위 벡터를 구하는데 성공했다.

ray.c

//광선이 최종적으로 얻게된 픽셀의 색상 값을 리턴.
t_color3    ray_color(t_ray *ray, t_sphere *sphere)
{
    double  t;

    t_point3 hit_point; // 레이가 부딪힌 지점
    t_vec3  normal_vec; // 법선 백터
    t_vec3  n;

    t = hit_sphere(sphere, ray);
    printf ("근 : %f\n", t);
    if (t > 0.0)
    {
        //정규화 된 구 표면에서의 법선
        // ray_at(ray, t) = ray->orig + vmult(ray->dir, t)
        // 원점 + 방향 * 길이 = O + D * t = P(t)
        hit_point = ray_at(ray, t); // 광선과 구체가 충돌한 교점
        normal_vec = vminus(hit_point, sphere->center); // vminus(P - C), 법선 벡터를 의미한다.
        n = vunit(normal_vec); // 표준화, 단위 백터가 된다.
        return (vmult(color3(n.x + 1, n.y + 1, n.z + 1), 0.5));
    }
    else
    {
        // (1-t) * 흰색 + t * 하늘색
            return (color3(0.5, 0.5, 0.5));
    }
}

vunit 을 통해 정규화 과정을 진행한다.

인자로 들어가는 저 백터가 의미하는 것은 vminus(ray_at(ray, t), sphere->center)는 법선 벡터를 의미한다.

정규화

모든 벡터는 정규화(normalize) 과정을 거쳐 단위 벡터로 만들 수 있다. 백터 U가 (x, y)라고 했을 때, 정규화 수식은 다음과 같다.

U = ({x\over\sqrt{x^2 + y^2}}, {y\over / \sqrt{x^2 + y^2}})

위 식은 벡터의 각 성분에 벡터의 크기를 나눠준 것이다!

백터의 크기

x, y 좌표에 있는 백터의 길이를 피타고라스의 정리를 이용해서 구할 수 있다.

벡터의 종점에 수선을 내려 직각삼각형을 만들면 벡터의 길이가 삼각형의 빗면이 되고, 피타고라스의 정리를 응용한 수식은 아래와 같이 된다.

x^2 + y^2 = z^2

\sqrt{x^2 + y^2} = z

코드로 구현한 벡터 정규화

// 벡터 길이 제곱
double      vlength2(t_vec3 vec)
{
    return (vec.x * vec.x + vec.y * vec.y + vec.z * vec.z);
}

// 벡터의 길이, x^2 + y^2 + z^2의 제곱근
double      vlength(t_vec3 vec)
{
    return (sqrt(vlength2(vec)));
}
// 단위 벡터
t_vec3      vunit(t_vec3 vec)
{
    double len = vlength(vec);
    if (len == 0)
    {
        printf("Error\n:Devider is 0");
        exit(0);
    }
    vec.x /= len;
    vec.y /= len;
    vec.z /= len;
    return (vec);
}

왜 법선 벡터를 구하고 정규화를 해주어야 하는가?

퐁 조명 모델에서 제대로 나오는 개념이라서 간단하게 짚고 넘어가겠다.

내적(난반사) 구하기

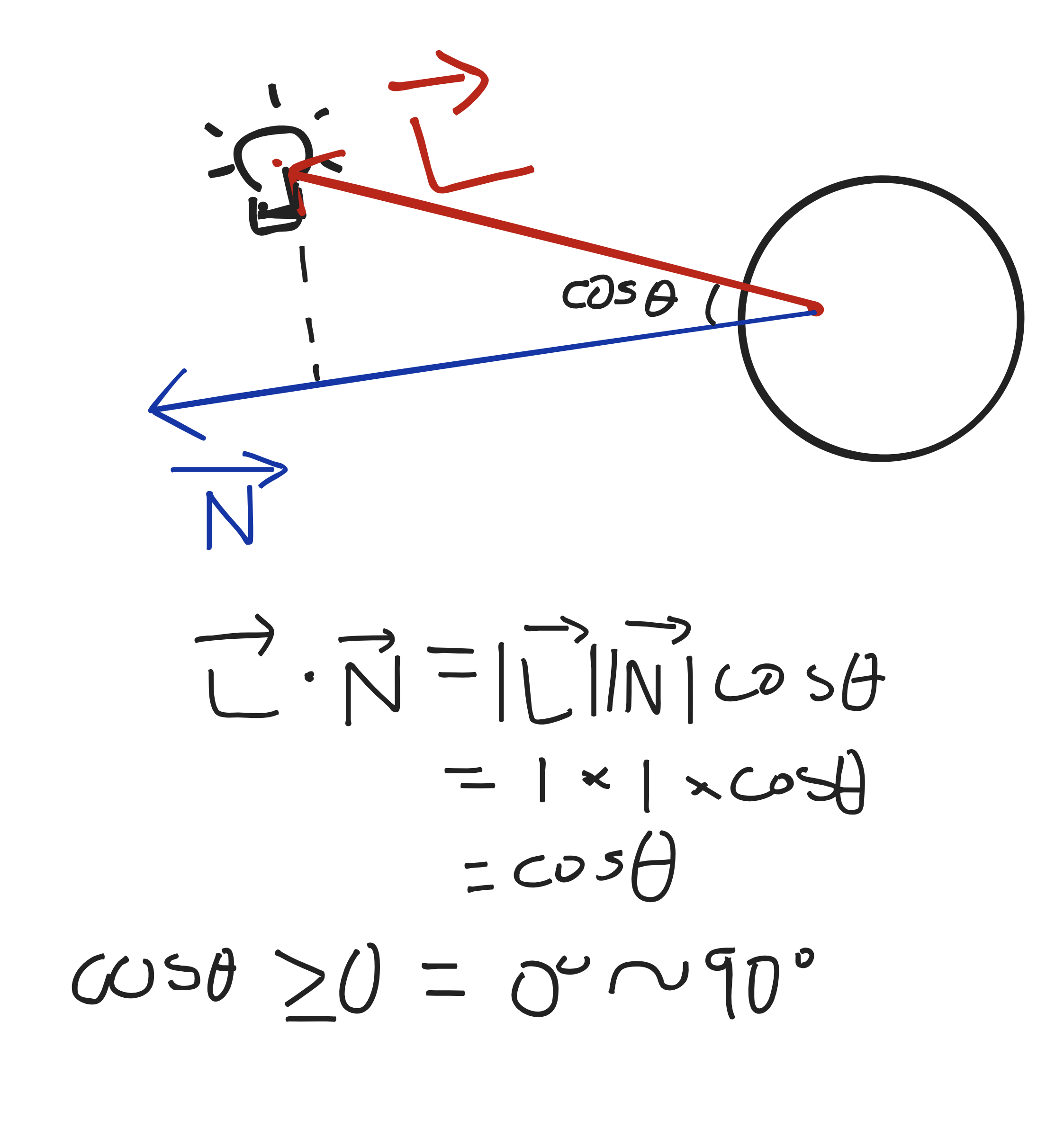
부딪힌 교점에서 뻗어나가는 법선벡터와 교점에서 광원까지의 벡터(정규화로 단위벡터화)를 내적하였을 때 나오는 결과값인 코사인 세타값을 이용해 난반사를 구현할 수 있다.

법선 벡터를 N이라고 하고 교점에서 광원까지의 벡터(단위 벡터)를 P라고 했을 때, N과 P의 내적 결과로 두 벡터가 이루는 사이각을 구할 수 있다. 사이각이 0도에 가까울 수록 해당 교점은 빛을 정면으로 받고 있다는 의미가 된다. 반대로 90도에 가까울 수록 빛을 거의 받지 못하게 되며 90도를 넘어가게 되면 광원의 영향을 아예 받지 못하게 된다고 판단할 수 있다.

외적(정반사) 구하기

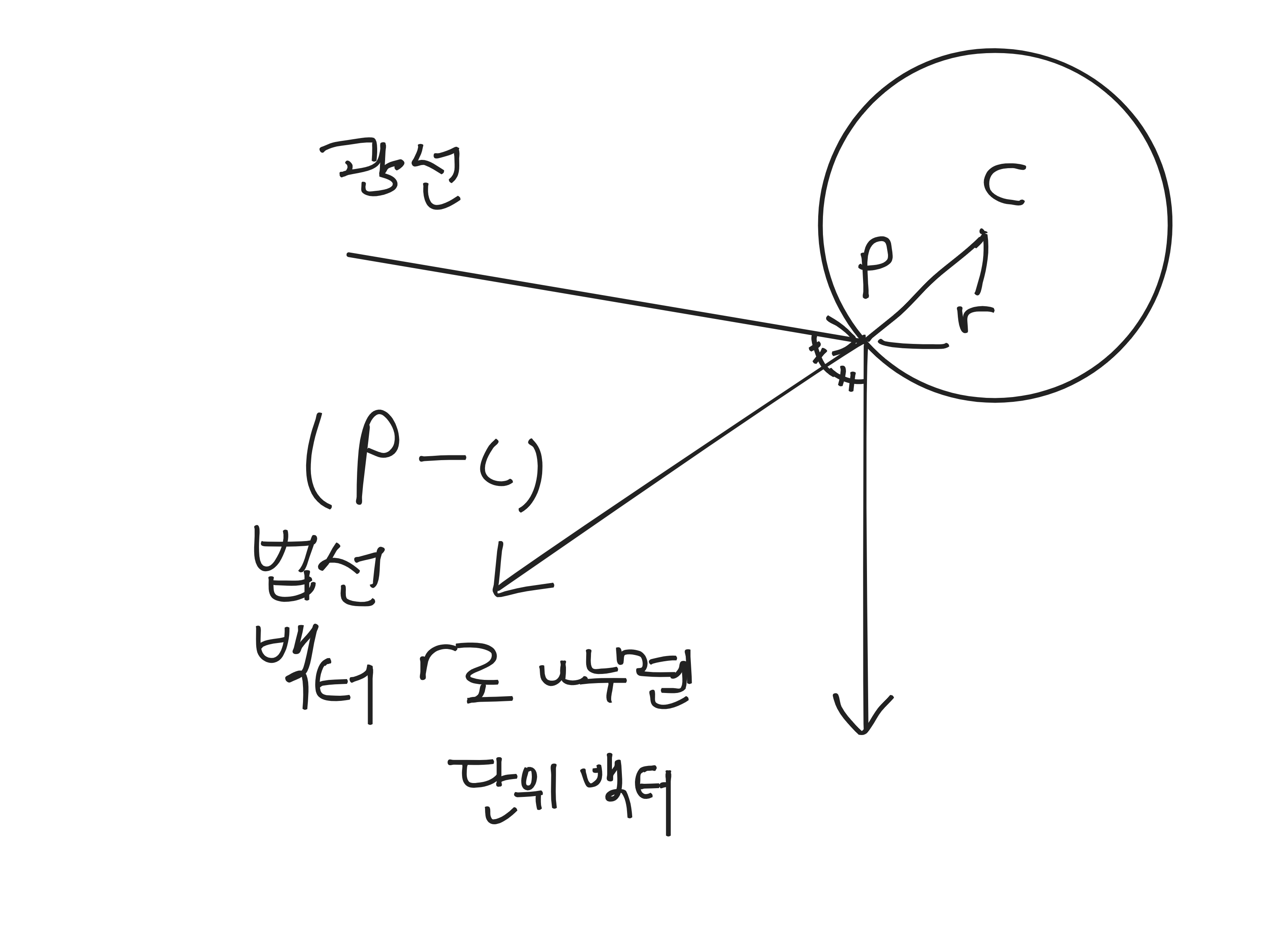
광선이 물체와 부딪혔을 때 부딪히는 것을 감지하는 데에서 끝나는 것이 아니라 표면에서 반사되는 것을 구현을 해야 한다.

벡터의 외적을 이용해서 광선이 어떻게 튕겨나가는 지를 구할 수 있다. 벡터의 외적은 또다른 벡터, 정확히 말하면 두 벡터에 수직인 벡터를 구하는를 구하는 연산인데, 그 벡터가 바로 튕겨져 나가는 방향을 의미하기 때문이다.

그를 위해서 필요한 것이 바로 법선 벡터이다. 법선 벡터는 표면적에서 수직으로 뻗어나가는 벡터인데, 해당 백터와 광선의 백터를 외적해주면 우리가 원하는 값이 나오게 된다.

그런데 외적을 해주기에 앞서, 우리는 광선에 대한 단위 벡터를 알고 있다. 그리고 외적의 중요한 특징 중 하나,

단위 백터끼리 외적한 결과는 언제나 단위백터다.

따지고 보면 당연한 것이, 단위 벡터는 벡터의 방향만을 나타내기 위해 크기를 1로 놓고 보기 때문에 똑같이 크기를 1로 놓고 보는, 오로지 방향만을 가리키는 단위 벡터 끼리의 외적 값은 단위 벡터가 나올래야 나올 수 밖에 없다.

법선 백터를 구하고, 또 정규화를 해야 하는 이유는 바로 빛과의 상호작용을 하기 위함이었다.

벡터의 내적과 외적

코드 수정 - 간단하게

기존 코드

double      hit_sphere(t_sphere *sp, t_ray *ray)
{
    t_vec3  oc; // 0에서부터 벡터로 나타낸 구의 중심.
    //a, b, c는 각각 t에 관한 근의 공식 2차 방정식의 계수
    double  a;
    double  b;
    double  c;
    double  discriminant; //판별식

    oc = vminus(ray->orig, sp->center);
    a = vdot(ray->dir, ray->dir); 
    b = 2 * vdot(oc, ray->dir);
    c = vdot(oc, oc) - sp->radius2;
    discriminant = (b * b) - (4 * a * c);
    printf ("a : %f, b: %f, c : %f, 판별식 : %f\n", a, b, c, discriminant);

    // 판별식(내적의 값)이 0보다 크다면 광선이 구를 hit한 것!
    // 내적이 양수 : cos 값이 양수, 예각
    // 내적이 0 : cos 값이 0, 직각
    // 내적이 음수 : cos 값이 음수, 둔각
     
     if (discriminant < 0) // 판별식이 0보다 작을 때 : 실근 없을 때,
        return (-1.0);
    else
        return ((-b - sqrt(discriminant)) / (2.0 * a)); // 두 근 중 작은 근
}

https://oopy.lazyrockets.com/api/v2/notion/image?src=https%3A%2F%2Fs3-us-west-2.amazonaws.com%2Fsecure.notion-static.com%2F0a1c3562-78a8-46f0-a072-784840dd0c42%2FUntitled.png&blockId=19a56118-c134-4f18-a25e-0b9120d1872d

여기서의 h, 즉 B 는 (O - C)와 단위 백터의 내적이다.

b의 값이 항상 2의 배수인데, 이를 수정해서 근의 공식을 간단하게 수정할 수 있다.

B = D \cdot (O - C) * 2

{B\over 2} = D \cdot (O - C)

수정 코드

double      hit_sphere(t_sphere *sp, t_ray *ray)
{
    t_vec3  oc; // 0에서부터 벡터로 나타낸 구의 중심.
    //a, b, c는 각각 t에 관한 근의 공식 2차 방정식의 계수
    double  a;
	double  half_b;    // b가 half_b로
    double  c;
    double  discriminant; // 판별식

    oc = vminus(ray->orig, sp->center);
    a = vdot(ray->dir, ray->dir);
    half_b = vdot(oc, ray->dir);
    c = vdot(oc, oc) - sp->radius2;
    discriminant = (half_b * half_b) - (a * c);
    printf ("a : %f, b: %f, c : %f, 판별식 : %f", a, half_b, c, discriminant);

    // 판별식(내적의 값)이 0보다 크다면 광선이 구를 hit한 것!
    // 내적이 양수 : cos 값이 양수, 예각
    // 내적이 0 : cos 값이 0, 직각
    // 내적이 음수 : cos 값이 음수, 둔각
     
     if (discriminant < 0) // 판별식이 0보다 작을 때 : 실근 없을 때,
        return (-1.0);
    else
        return (-half_b - sqrt(discriminant / a)); // 두 근 중 작은 근
}