그래픽은 그럴듯하게 보이는 것이 중요하다
개요
다음 실습 예제를 따라가면서 퐁 조명 모델(phong model)이라는 생소한 개념이 등장했다. 이를 조사하면서 조명을 간단하게 표현하기 위해 사용하는 모델이라고 이해했고, 이 모델을 이용해서 레이 트레이싱을 구현하고 있다고 나는 생각했었다. 그러나 동료들에게 물음을 구한 결과 나의 이해는 완벽하게 엇나갔다는 것을 알게 되었다. 퐁 모델로 난반사를 구현하게 된다면 그것은 레이 케스팅이라고 할 수는 있어도 레이 트레이싱이라고 할 수 없다는 것이다.
그래픽은 그럴듯하게 보이는 게 핵심
굴절이나 정반사광 같은 경우에는 명확한 공식이 존재한다. 그러나 이를 제외한 나머지 것들은 어떤 공식을 쓰던 그럴 듯하게 보이기만 하면 된다.
mini_raytracing_in_c (8) Phong lighting
정반사와 난반사, 주변광은 phong model에 한정해서 쓰이는 개념이 아니다
난반사광과 정반사광에 대한 개념부터 다시 잡아야 했다. 내가 이해한 난반사광은 광원에서부터 표면이 빛을 얼마나 받는지를 계산한 것이라고 생각했다. 정반사광은 빛이 반사되었을 때 카메라에 들어오는 빛을 정반사광이라고 생각했다. 이 두가지 개념이 퐁 조명 모델에서만 유일하게 사용되는 개념이라고 생각했다.
그러나 실제 정반사와 난반사는 표면이 울퉁불퉁한지 매끈한지에 따라 빛이 어떻게 퍼져나가는지에 대해 구분한 광학적인 개념이었다. 반사되는 표면이 거울처럼 매끄럽다면 어느 위치에서던 같은 각도로 빛은 반사가 되고, 이를 정반사라고 한다. 반사되는 표면이 울퉁불퉁하다면 빛은 이리저리 튀며 각기 다른 방향으로 반사가 되고, 이를 난반사라고 한다. 밑의 그림처럼 말이다.
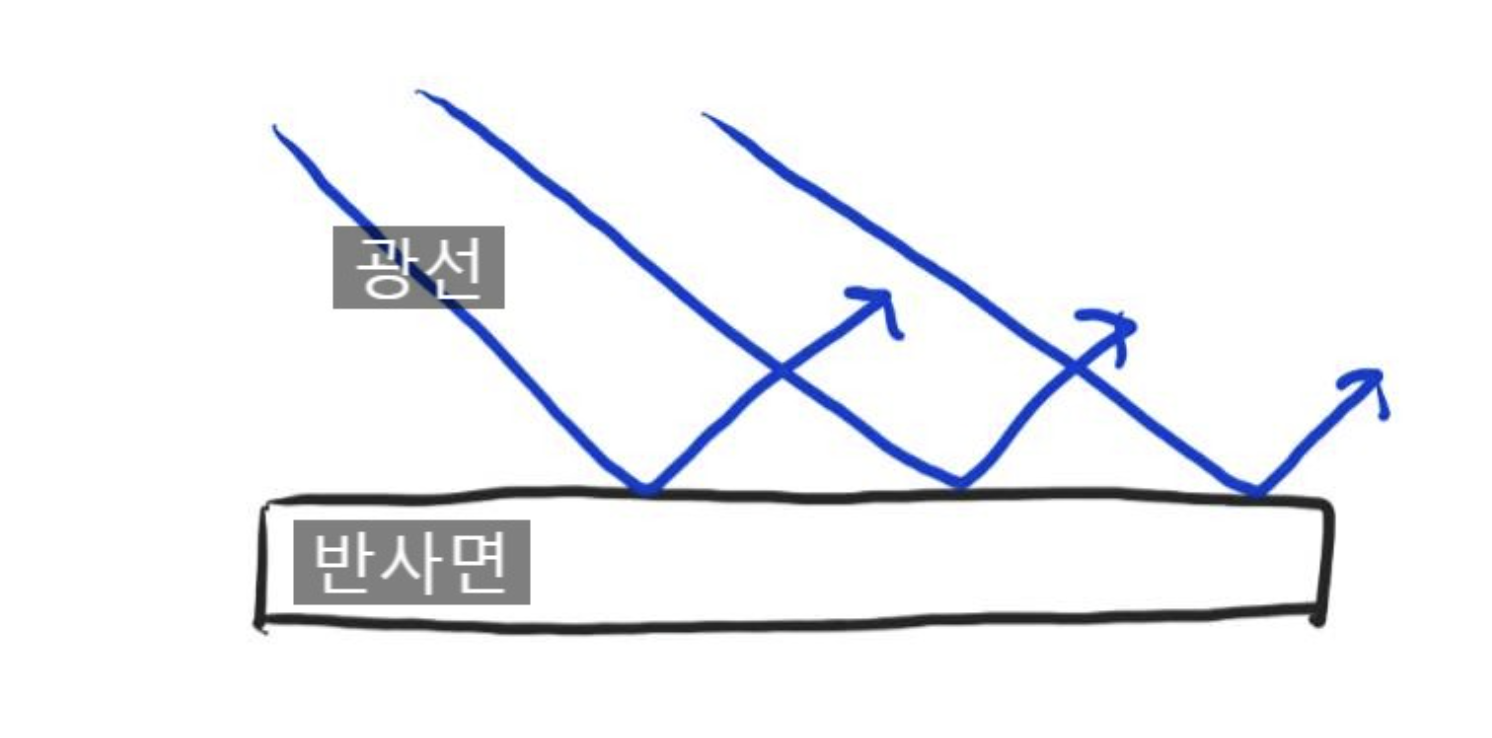

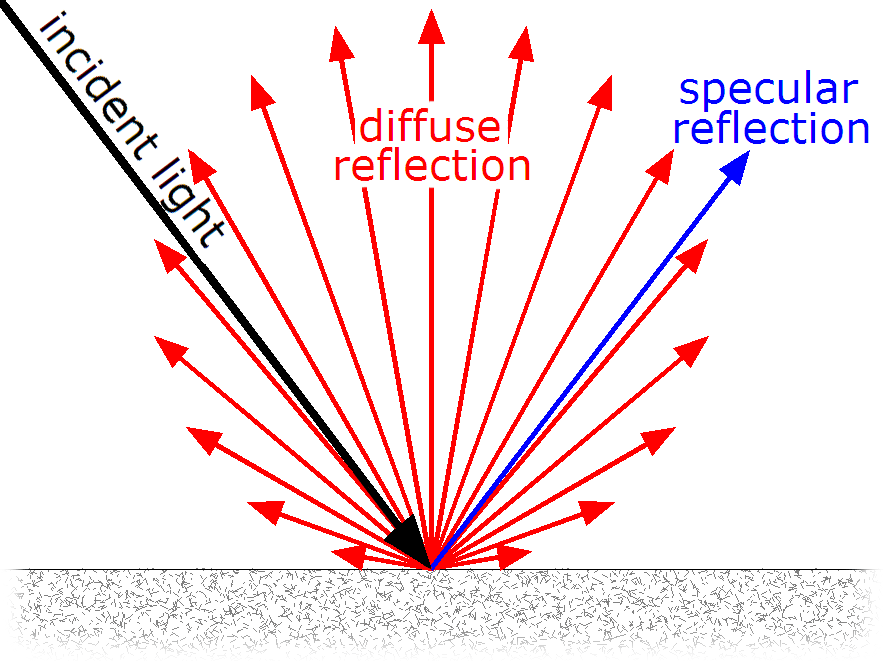
실제 난반사광, 정반사광처럼 구현한다는 것은 특정 물체가 얼마만큼의 난반사광 비율과 정반사광 비율을 가지고 있는 지에 대해서 구하는 것이 된다.
[물리학][광학] 1. 빛의 반사 - 정반사, 난반사, 반사의 법칙, 반사파
단순화를 위한 phong model
퐁 조명 모델은 광원을 받는 어떤 물체를 표현할 때 주변광(Ambient) 난반사광(Diffuse), 정반사광(Specular), 방사광(Emission) 이 네 가지를 전부 합쳐서 표현하는 하나의 방식인 것이다.
굴절되는 벡터와 광원과의 벡터의 유사성
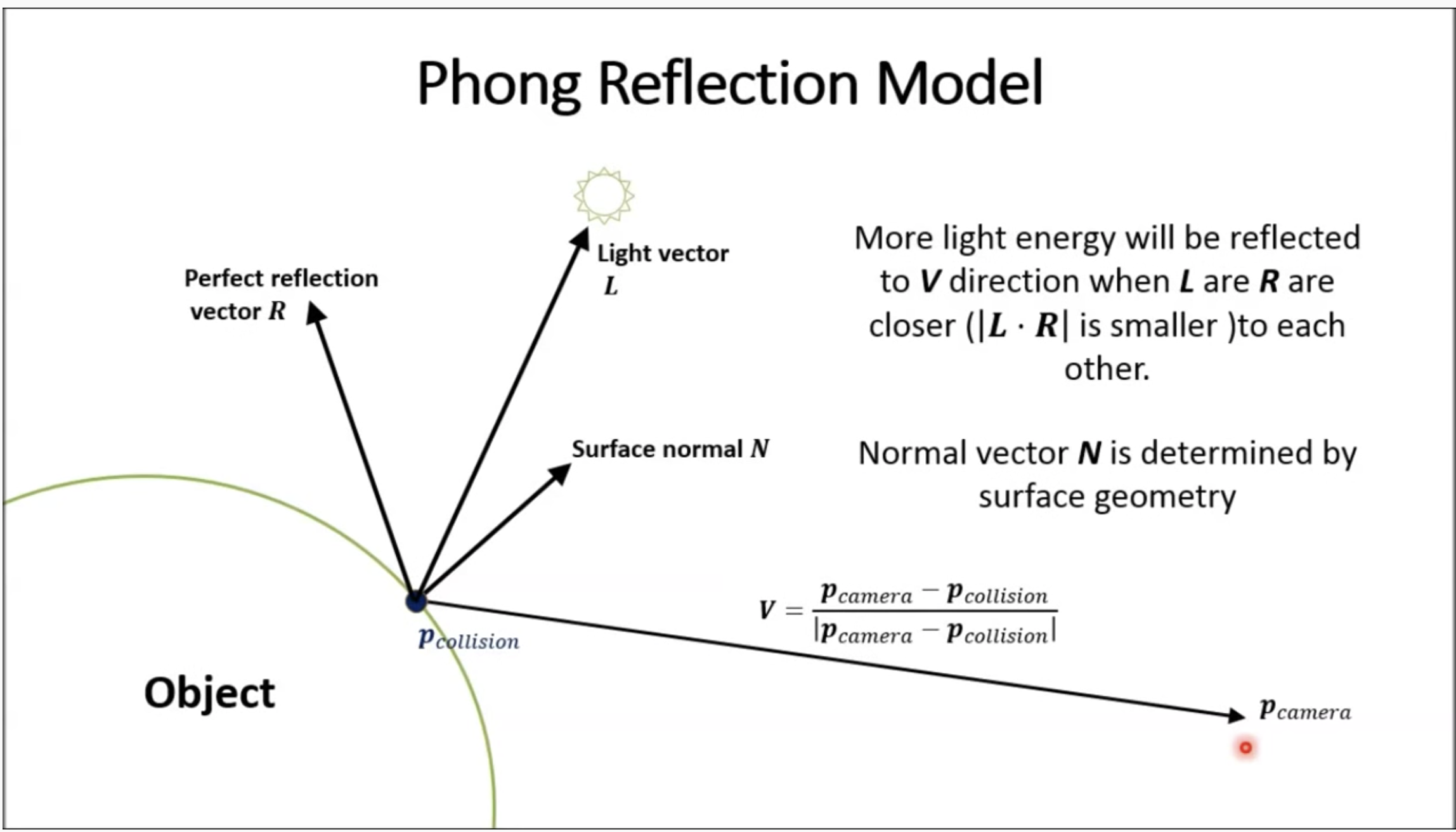
광원이 없다면 광선이 물체와 충돌했다고 한들 까맣게 보이는 것이 정상일 것이다.
광선을 쏘아 물체와 충돌한 후 해당 광선이 광원에 충돌해야 빛을 받아서 물체 고유의 색깔을 반사할 수 있게 되는 것이다. 퐁 조명 모델은 정반사와 난반사 모두 위의 공식을 이용해서 구현을 하게 된다. 충돌지점과 광원을 내적하여 사이각을 구하고 사이각이 작을 수록 빛을 난반사를 많이 받는다 가정하고, 광선이 굴절한 후 광원과 유사하다면 정반사를 받는다고 가정하는 것이다.
forward ray tracing, backward ray tracing
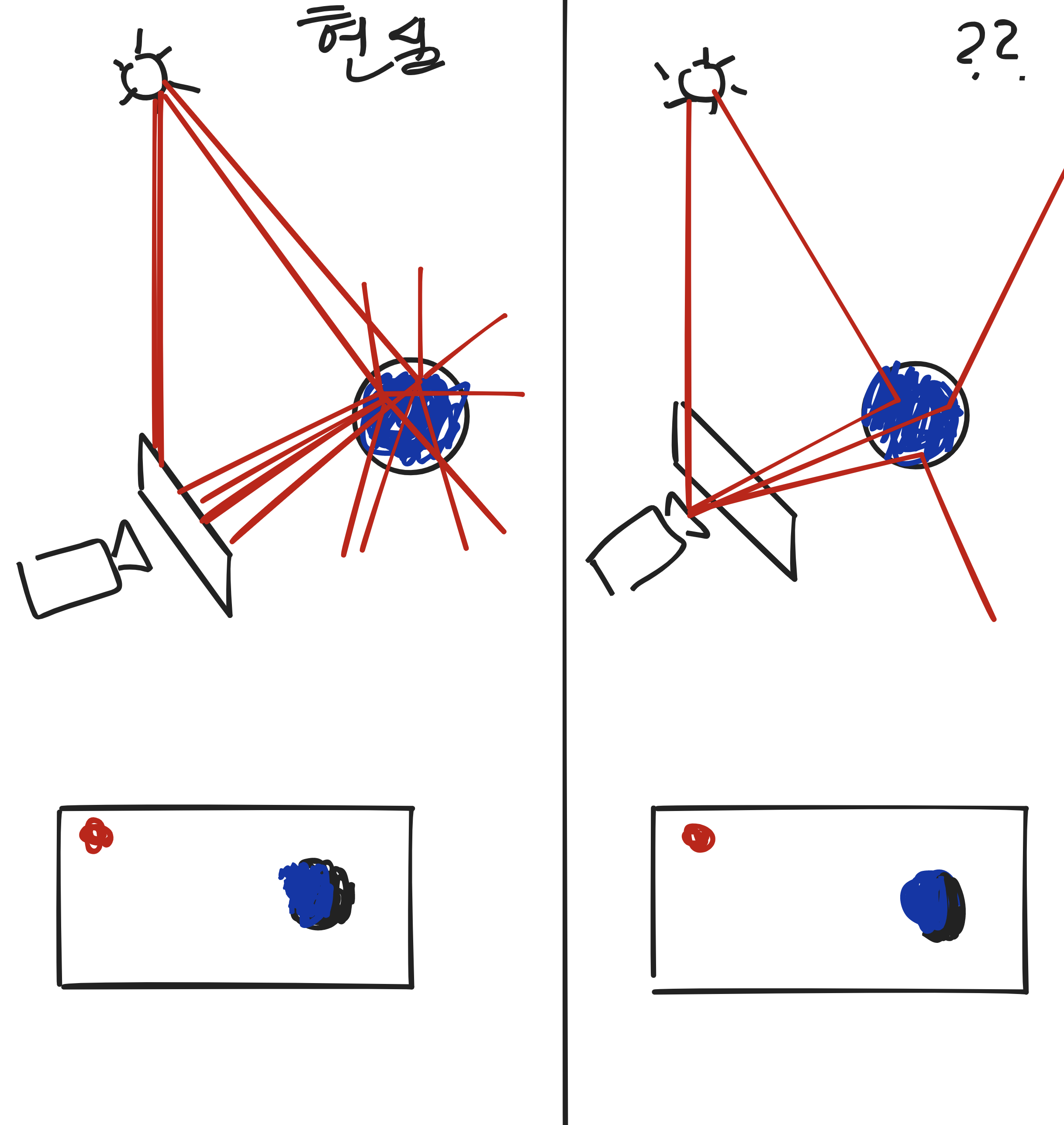
그런데 뭔가 이상하다. 잘 생각해보면 카메라에서 광선을 쏘아서 충돌된 광선이 굴절하여 광원에 닿아 빛을 반사하는 게 아닌, 반대로 광원에서부터 수많은 광선이 나오고 그 중 카메라와 직접적으로 충돌하게 되면 해당 픽셀은 광원의 색(하얀색)이, 그 중 물체와 충돌한 후 굴절하여 카메라에 충돌하면 해당 픽셀은 물체의 색만을 반사하여 물체의 색을 띄게 되는 것이 현실적이지 않은가? 왜 반대인 카메라에서 광선을 나가는 것처럼 생각하고 있었을까?
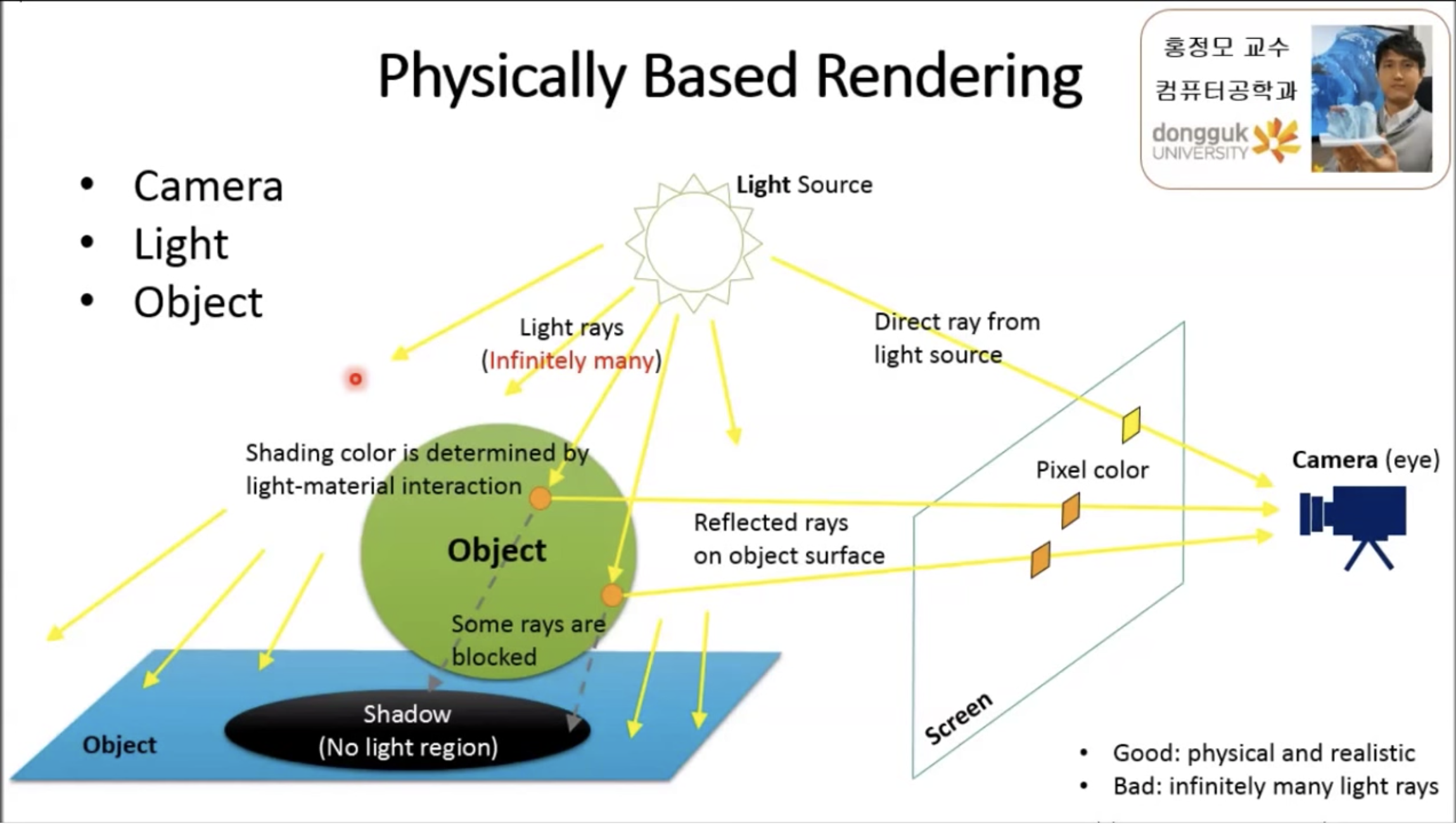
현실처럼 광선에서부터 광선을 쏘는 빛 추적 방식을 forward ray tracing이라고 하는데, 실제 세계의 빛의 흐름을 더 정확하게 모델링하는 방식으로 최종적으로 뷰포트(카메라)에 들어온 빛이 픽셀로 변환된다. 물리적이고 사실적이라는 장점이 있지만 빛의 광선을 전부 계산해야 하기 때문에 연산이 늘어난다는 단점이 있다.
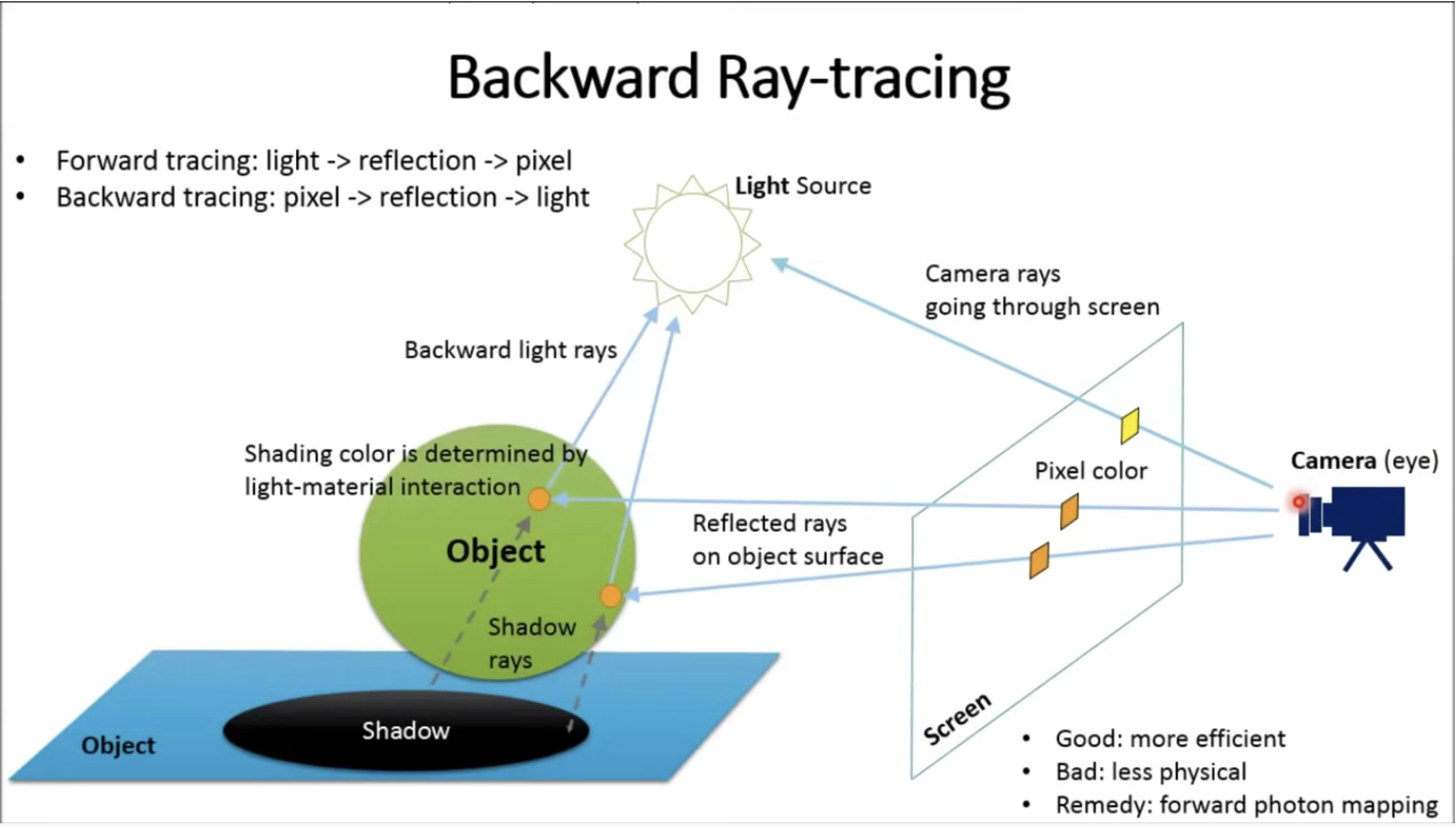
반대로 카메라에서 광선을 쏘는 빛 추적 방식을 backward ray tracing이라고 하는데, 실제 카메라를 통해 보는 화면(캔버스, 모니터)를 가상화한 뷰포트의 각 픽셀 하나하나에서 광선을 쏘아서 무엇을 충돌하냐에 따라 픽셀을 구성하는 방식이다. 위의 방법보다는 덜 현실적이지만 효율적으로, 연산을 크게 줄인다는 장점이 있다.
퐁 조명 모델에서 구현하는 난반사
실제 난반사처럼 구현한다면 해당 교점에서 랜덤한 벡터로 빛이 튕겨져 나가고, 레이 트레이싱이기 때문에 튕겨져나간 빛이 다른 물체에 충돌할 때 해당 충돌점에서 또 랜덤한 벡터로 튕겨져 나가는 빛을 계산하는 방법을 쓸 수 있을 것이다. 그러나 퐁 모델로 난반사를 구현하게 된다면 광원에서 빛이 나와서 물체에 반사되어 눈에 들어오는 단계만 수학적으로 계산하게 된다.
그렇다면 퐁 조명 모델에서 난반사를 구하는 공식은 어떻게 되는가?
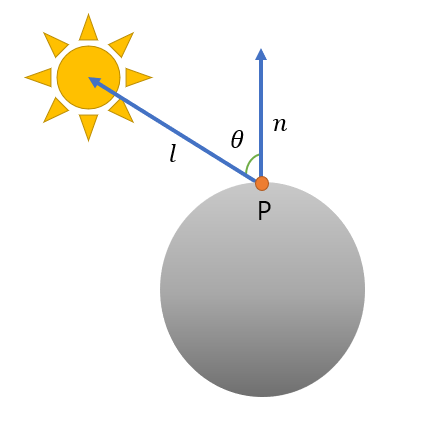
퐁 조명 모델에서의 난반사는 광원에서부터 교점까지의 벡터와 교점의 법선 벡터의 내적을 구했을 때, 두 벡터 전부 표준 벡터라는 가정하에 결과 값인 코사인 세타를 통해 사이각을 구하고, 해당 사이각이 0, 수직에 가까울 수록 빛을 많이 받고 있다는 의미가 된다.
물리적으로 올바르지 않고, 빛을 계속해서 추적하지도 않기에 레이 트레이싱이라고 하기에는 애매하지만, 적은 연산으로 그럴 듯하게 보이게끔 구현한다는 점이 핵심인 것이다.
minRT 자료를 찾아보면서 빛의 구현 부분에도 내용이 차이가 나는 부분을 발견한 이유도 이것 때문이었다.
빛의 반사를 구현할 때 퐁 조명 모델로 간략하게 구현했는가 실제 난반사처럼 구현했는가에 따라 코드가 다를 수 밖에 없었던 것이다.
퐁 조명 모델을 사용한 예제
mini_raytracing_in_c/08.phong_lighting.md at main · GaepoMorningEagles/mini_raytracing_in_c
실제 난반사처럼 구현한 예제(재귀)
(9) Raytracing One Weekend 식 이해하기! 6
ray tracing과 ray casting, path tracing과 phong model
용어에 대한 정리로 마무리를 하자.
ray tracing
가상의 광선을 발사하고 광선이 물체와 충돌하면 현실처럼 다시 반사되는 빛을 재귀적으로 연산하여 이미지를 렌더링하는 기법. 반사되는 횟수가 일정 횟수에 도달하거나 반사된 광선이 그 어떤 물체와도 충돌하지 않게 되는 것이 재귀의 종료 조건이 된다.
ray casting
가상의 광선을 발사해서 광선이 물체와 충돌하였을 경우 물체까지와의 거리를 토대로 이미지를 렌더링하는 기법. 광선이 물체와 충돌하기까지의 거리를 계산할 뿐 더 이상의 연산을 수행하지 않는다.
path tracing
빛이 반사되었을 때의 경로를 추적해서 재귀적으로 렌더링한다는 점에서 ray tracing과 결과적으로는 같다고 할 수 있다. 그러나 ray tracing이 각 픽셀을 렌더링하기 위해 하나의 광선을 쏘아서 굴절, 반사의 경우에만 추가적인 광선을 쏘는 반면 path tracing은 반사, 굴절이 없는 물체에도 추가적인 광선을 쏘아서 모든 물체가 빛을 반사하고 흡수하는 현실의 빛 효과를 완벽하게 따라한다. 그렇기에 path tracing은 하나의 픽셀을 렌더링하기 위해 하나의 광선이 아닌 수십, 수백 개의 광선을 쏘게 된다.
https://www.youtube.com/watch?v=frLwRLS_ZR0
