들어가며
ALU는 "Arithmetic Logic Unit"의 약자로, 컴퓨터의 중요한 구성 요소 중 하나입니다. ALU는 CPU (Central Processing Unit)의 핵심 부분 중 하나로서 산술 및 논리 연산을 수행하는 장치입니다. 주요 역할은 다음과 같습니다:
산술 연산: ALU는 덧셈, 뺄셈, 곱셈, 나눗셈과 같은 산술 연산을 처리합니다. 이러한 연산은 CPU가 숫자를 계산하고 수학적 연산을 수행하는 데 필요합니다.
논리 연산: ALU는 논리 연산자(AND, OR, NOT, XOR 등)를 사용하여 비트수준의 논리 연산을 수행합니다. 이는 조건을 평가하고 논리 게이트를 사용하여 프로그램의 제어 흐름을 조작하는 데 사용됩니다.
-chatGPT
ALU 산술 연산, 논리 연산들 도와주는 연산기이다. 이전까지 알아본 1 bit full adder와 다른 서킷들을 합쳐서 구성되어 있으며 점차적으로 진화된 형태를 띈다.
2진 연산 방식
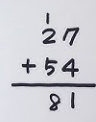
우리가 10진수 연산을 할 때 연산을 어떻게 할까? 위 그림을 보면은 첫째 자리수 7과 4를 더해서 11이 나오지만 한 자리로는 표현할 수 없어서 1을 다음자리로 넘기고 있다. 이렇게 다음 자리로 올라가는 수를 우리는 올림수라하고 영어로는 Carry out이라고 한다. 둘째 자리수 입장에서는 2와 5를 더하면 되는데 올림수가 올라왔고 올라온 수를 Carry in이라고 한다. 똑같은 올림수인데 어느 시점에서 바라보냐에 따라서 용어가 다르다
2진 연산도 마찬가지이다. 하나의 자리에서 표현할 수 있는 수는 0과 1이다. 그래서
1 + 1 = 2
는 2진수에서는 표현하지 못하는 방법이고 1을 다음 자리로 올려줘야한다. 마치 10진수에서 한 자리로 10을 표현하지 못해서 1을 다음 자리로 올리듯이 말이다.
Overflow
덧셈기와 뺄셈기에서 오버플로우는 언제 발생하는지 알아보자.
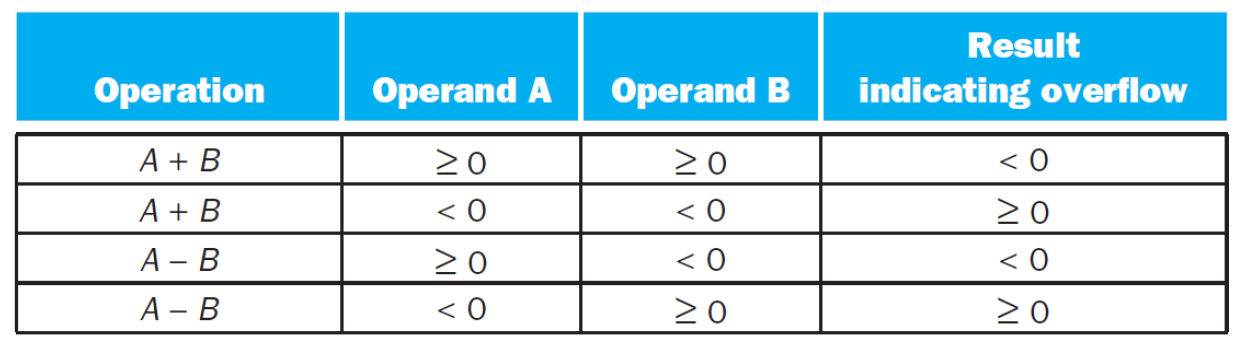
먼저 Overflow란 현재 가지고 있는 비트로는 연산 결과를 표현할 수 없을 때 발생하는 현상이다. 예를 들어 Singed 3비트 체계에서는 표현할 수 있는 수가 -4 ~ 3 까지이다. 그런데 2 + 2를 하면 어떨까? 4는 표현할 수 없는 수이고 2비트로 나타내면은 100 이다. 하지만 Signed 3비트 체계에서 100 은 -4이다. 즉, 4는 표현할 수 없는 수이고 이런 경우에 연산 결과로 오버플로우가 발생했다고 한다.
덧셈기에서 오버플로우는 서로 같은 부호를 더했을 때 발생할 수 있다.
뺼셈기에서 오버플로우는 서로 다른 부호를 뺄 때 발생할 수 있다.
우리는 여기서 조금 더 Overflow에 대한 일반화된 규칙을 만들어낼 수 있다.
Rule of thumb
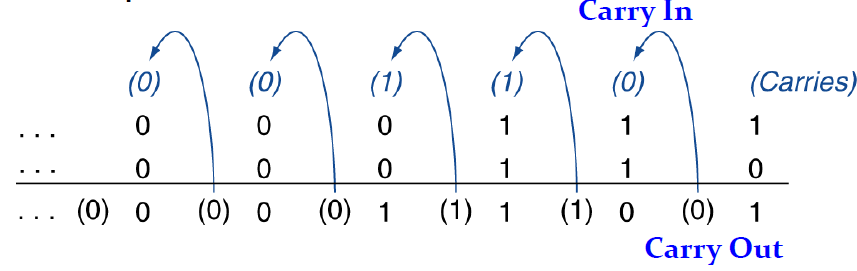
N비트 덧셈 혹은 뺄셈을 할 때 마지막 ALU의 Carry in과 Carry out이 다르다면 우리는 그 때 Overflow가 발생했다고 볼 수 있다.
요약. 마지막 ALU의 Carry-in 과 Carry-out이 다르다면 Overflow가 발생
ALU
ALU는 단순히 덧셈, 뺄셈 처럼 산술연산만 가능한게 아니라 논리 연산도 가능하다. AND, OR, NOT, NAND, NOR처럼 말이다. 어떻게 ALU가 이렇게 다양한 연산을 할 수 있는 지를 점차적으로 알아보자. 핵심 키워드는 MUX이다.
AND, OR
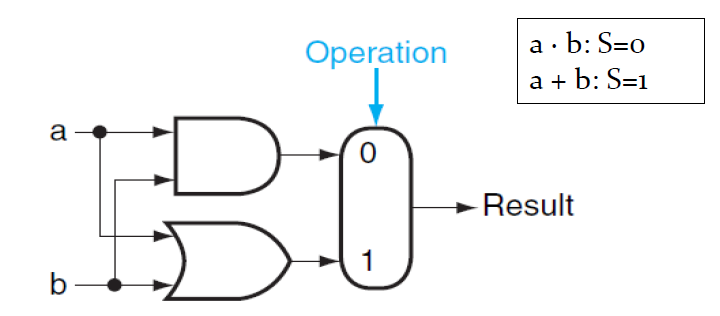
먼저 AND, OR 연산을 하는 서킷이다. a랑 b랑 AND연산의 결과를 MUX의 0과 매핑을 하고 OR연산을 할 때는 1과 매핑을 한다. 그럴 시에 MUX에 0을 인가하면은 AND연산을, 1을 인가하면은 OR연산을 수행한다.
ADD
이전 연산기에서 ADD연산을 수행하도록 서킷을 확장해보자.
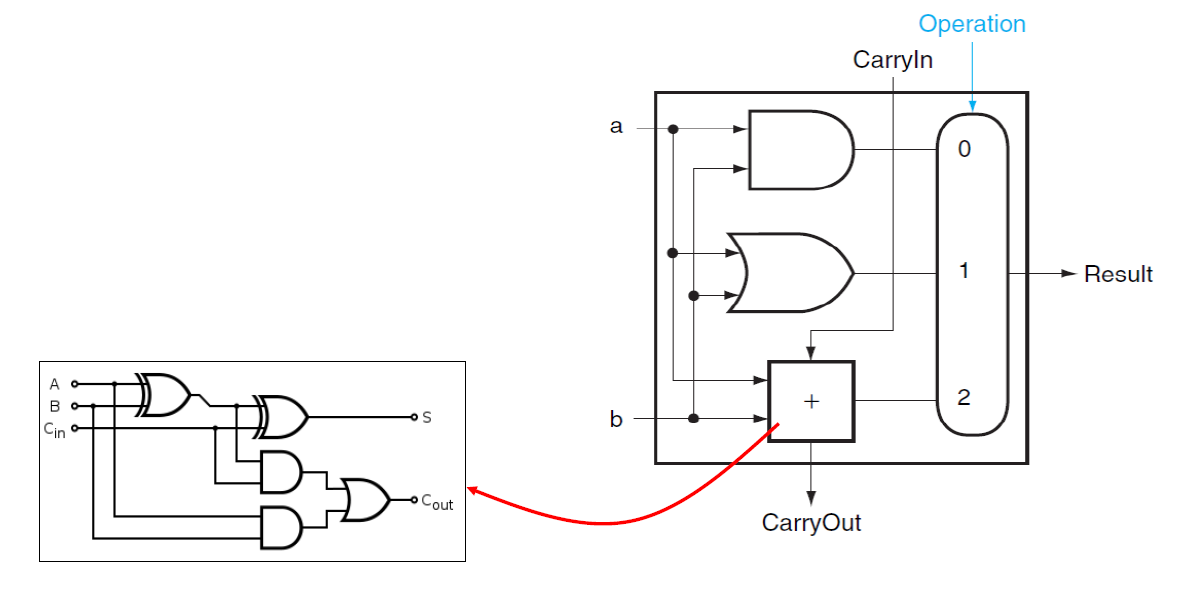
기존에 있었던 AND와 OR 서킷에는 손댄 부분이 하나도 없다. 단지 덧셈기를 하나 추가하고 MUX의 크기도 늘렸다. 이제는 MUX에 2를 인가하면은 덧셈기로 작동한다.
기존과는 다르게 덧셈기를 위해 Carry-in과 Carry-out이 추가되었음을 알 수 있다.
복습하자면, 덧셈기에서 Sum은 A, B, Carry-in의 XOR연산으로 구할 수 있고 Carry-out은 A, B의 XOR 연산과 AND연산의 값들을 OR 연산으로 구할 수 있다. 둘의 공통 연산으로 A, B의 XOR연산을 엿볼 수 있다.
32비트 덧셈기
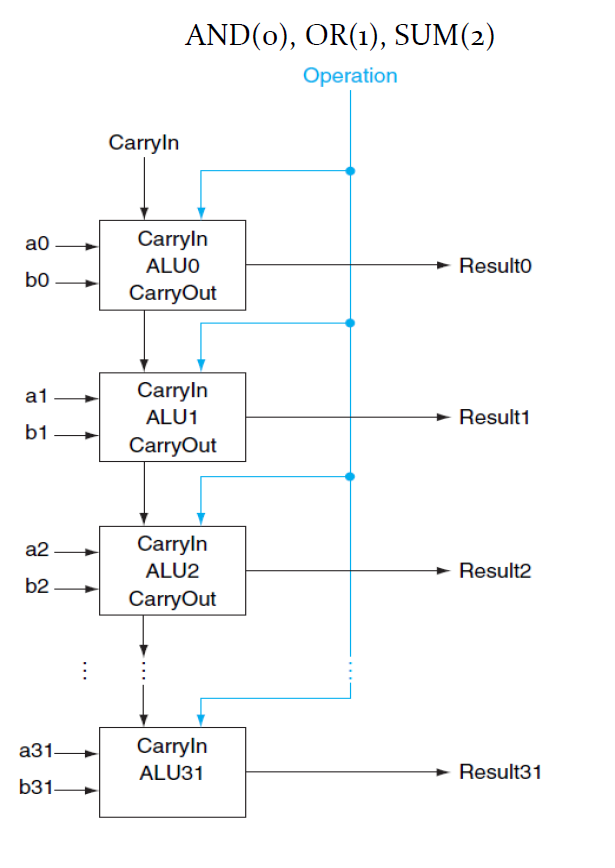
각 ALU에는 이전 ALU의 Carry-out이 Carry-in으로 들어온다. 그리고 모든 ALU의 MUX에는 같은 신호 (Operation)이 들어와야 한다.
SUB
AND, OR, ADD 연산을 하는 ALU에 뺄셈 기능을 추가해보자.
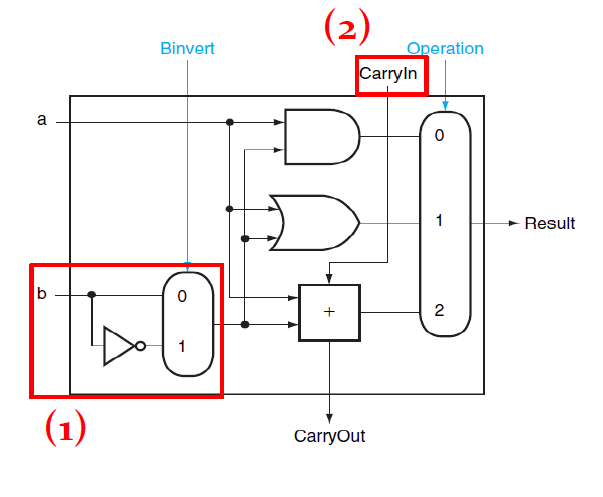
A-B는 A + !B + 1로 볼 수 있다. 2의 보수를 활용한 방법이다.
B의 보수는 NOT 연산으로 쉽게 구할 수 있다. 그래서 B의 input 바로 앞에 MUX를 추가해서 NOT연산을 수행할 수 있게 한다. 그런데 B의 보수 뿐만 아니라 1을 더해주어야 뺄셈이 구현이 된다. 어디서 1을 가져올 수 있을까?
답은 바로 첫번째 ALU의 Carry-in에 있다. 기존의 ALU에서는 Carry-in이 무조건 0이다. 왜냐하면 첫째 자리는 올림수를 받을 일이 없기 때문이다. 하지만 첫번째 ALUdml Carry-in에 1을 인가해주면은 뺄셈 연산에서 필요한 기능을 얻을 수 있다.
NOR, NAND
NOR과 NAND는 어떻게 구현할 수 있을까? 이 때는 드모르간 법칙을 이용한다.
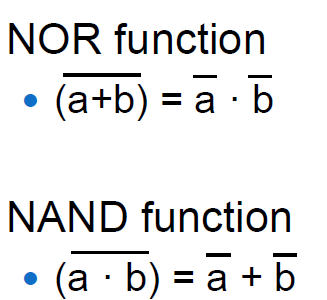
a와 b의 XOR은 !a, !b의 AND연산으로 구할 수 있다. b의 보수는 SUB연산에서 인버터와 MUX를 추가했기 때문에 구할 수 있다. 이번에는 a의 input에 인버터와 MUX를 추가하자.
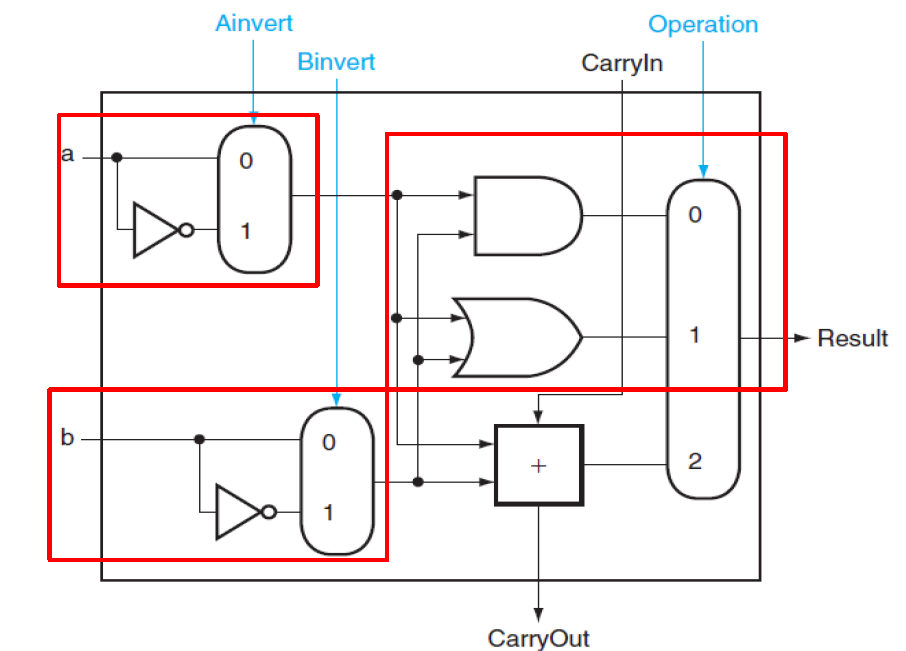
a와 b의 XAND는 어떻게 구할까? a, b의 MUX에 각각 1을 인가하고 Operation을 1로 인가(OR연산)하면 된다.
SLT - for Condition code
SLT는 Set on Less Than의 약자이다. 이제 마지막으로 ALU에 하나를 추가할건데 그게 뭐냐면 Less이다.
Less를 추가하는 이유를 설명하자면 바로 condigion codes 중에서는 Negative를 구하기 위해서이다.
Negative를 구하는 방법은 다음과 같다.
- 모든 ALU의 less값은 0으로 인가된다. 그리고 less에는 어떠한 논리, 산술연산도 들어가지 않는다. 즉, 모든 less값은 0으로 출력된다.
- 마지막 ALU의 Sum이 Set이라는 이름으로 첫번째 ALU의 less값으로 들어갈 수 있다. 마지막 ALU의 Sum은 다시 말해서 MSB의 비트값이고 이는 곧 "부호"를 의미한다.
- 결론적으로 less연산을 할 때는 MSB의 값이 첫번째 ALU의 less로 들어가고 less 연산의 결과는 000...0 이거나 000...1이다. 전자이면 양수, 후자이면 음수이다.
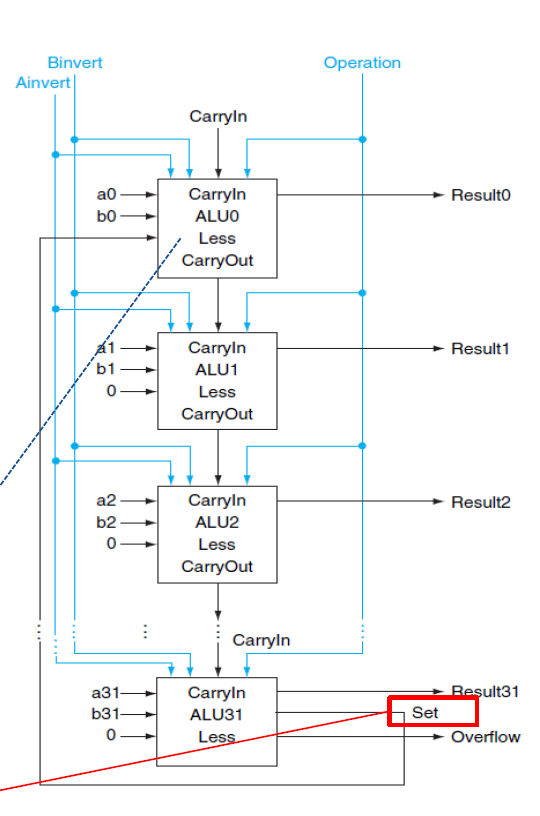
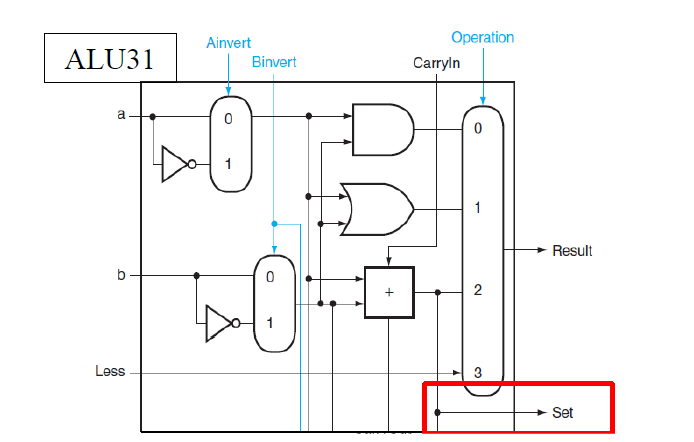
ALU - condition code
지금까지 ALU가 만들어지는 과정에 대해서 살펴보았다. 자 그러면 ALU에서는 어떻게 condition code를 만들어내는지 살펴보자.
먼저 condition code는 총 가지이다.
- Overflow
- Carry
- Negative
- Zero
3가지는 이미 살펴보았다. 먼저 Overflow는 마지막 ALU의 Carry-in과 Carry-out의 값이 다르면 Overflow이다.
Carry는 마지막 ALU의 Carry-out이다.
Negative는 SLT 전략을 이용해서 구할 수 있따.
자 그러면 마지막으로 Zero는 어떻게 구할까?
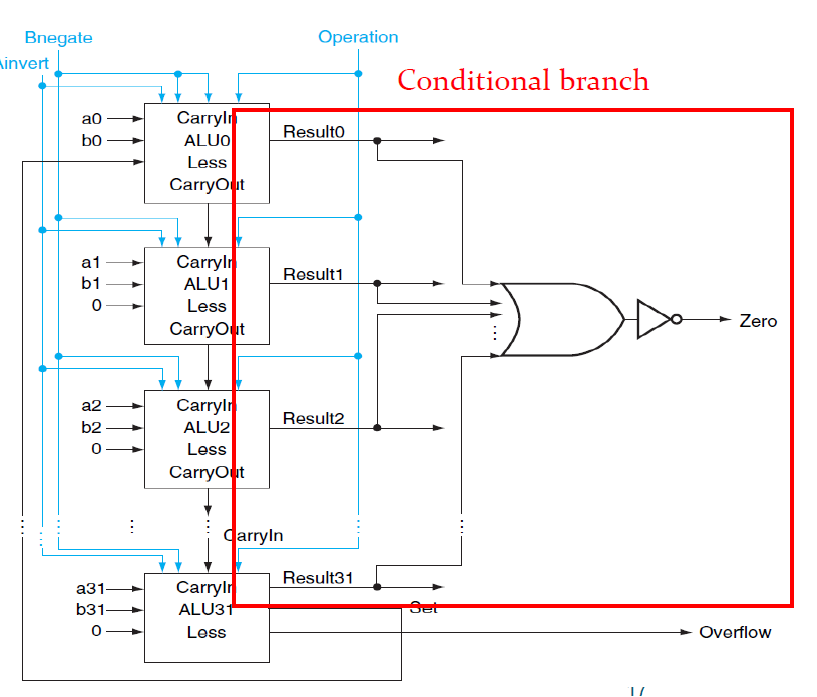
Operation에 ADD가 인가되어서 덧셈 연산을 하면은 Result가 여러 비트가 나오게된다. 모든 비트들이 0이면은 AND연산을 했을 때에도 0이 나온다. 그러면 이는 곧 결과값이 zero라는 뜻이다. 단 하나의 결과값이라도 1이면은 AND연산시에 1이 나온다.
Zero는 AND연산값에 보수를 결과값으로 제공한다. 즉, 모든 비트가 0이면은 Zero는 1이다.
