CS224W의 Community Structruture in Networks 강의와 Spectral Clutering 강의 부분을 정리한 글입니다.
아래 4가지 알고리즘에 대한 내용을 알아봄
- Louvain 알고리즘
- BigCLAM
- Spectral Clustering
- Motif-based Spectral Clustering
1. Community Structruture in Networks
Granovetter Theory
- 커뮤니티 탐지는 서로 밀집하게(densely)하게 연결된 노드를 구분하는 것이 목적
Q. 사람들은 개인적인 소개로 구직 정보를 얻을 때 어떻게 정보를 얻을까?
→ 친구보다는 지인을 통해 정보 얻음
친한 친구보다 지인을 통해 직장을 찾는 것은 friendships에 두 가지 측면이 있다는 것을 말함
- (1) Structural : 링크가 어떤 부분을 연결하는가?
- (2) Interpersonal : 어떤 링크가 더 강하고 약한가?
Structural role : Triadic Closure(= High Clustering Coefficients)
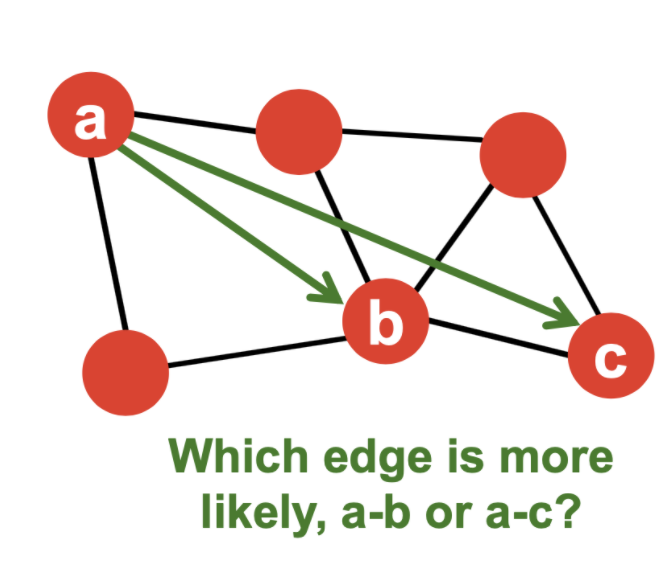
a-c보다 a-b가 두 명의 공통 노드를 공유하기 때문에 더 연결될 가능성이 높은 edge 임
Granovetter의 설명(Granovetter Theory)
- 사회 구조의 edge가 연결되는 role은 구조적, 정보적 측면에서 정의
- Structural
- 구조적으로 가까운 edge들은 사회적으로도 강하게 연결
- 서로 다른 네트워크를 연결하는 장거리 edge들은 사회적으로도 약하다
- Information
- 구조적으로 가까운 edge 들은 정보가 중복됨
- 장거리 edge들이 다른 부분에서 새로운 정보를 얻게 해줌(지인)
- Structural
2. Network Communities
Modularity
-
Granovetter Theory에 따르면 Network는 강하게 연결된 노드의 집합
-
Nework Communities
- 내부적으로 연결된 많은 노드들과 몇개의 외부적인 노드들로 이ㅣ루어진 집합
-
Modularity Q
-
노드간의 연결성 나타내는 Metric, 네트워크가 커뮤니티로 얼마나 잘 나뉘어졌는지 측정하는 척도
-
위의 Expected term을 찾기 위해 Configure model(null model) 사용
-
Modularity 의 특징은 [-1,1] 구간 값을 가짐
-
해석은 음수면 서로 상관 관계가 거의 없고, 0.3~0.7정도면 의미있는 커뮤니티 정보라 볼 수 있음
-
- 2m 은 normalize constant를 위한([-1,1] 구간으로 만들기 위한) 정규화 상수
- 는 연결되어 있으면 ? 1 아니면 0
Modularity 는 아래 식으로 다시 나타낼 수 있음(증명 생략)
- : 노드 i와 j 사이의 Edge weight
- : 그래프 안의 모든 edge weight의 합
- : 두 노드가 같은 커뮤니티면 1, 아니면 0
3. Louvain Algorithm
- 커뮤니티 탐지를 위한 greedy algorithm. 시간 복잡도 O(nlog(n))
- weighted graph에 사용하며 hierarchical community를 찾을 수 있다함
- Large graph 에서 성능이 잘 나온다함
- 두 phase로 이루어진 학습과정을 통해 greedy하게 modularity를 최대화 하는 알고리즘임
non-overlaps 알고리즘 설명
phase1
1) 각 노드가 single community라 생각
2) 노드 i를 어떤 이웃 j의 community에 넣으면 modularity값이 얼마나 증가하는 지 를 측정
3) 노드i를 가장 큰 를 발생시키는 community 로 이동 시킴
4) 변화가 없을대까지 phase1를 반복
phase2
1) phase1의 결과 얻은 communities를 모아 single super node를 만듬
- super-node 사이에 하나의 edge라도 있으면 연결
- 두 sper-node 사이에 edge 가중치는 커뮤니티 간 모든 edge 가중치의 합
2) 다시 phase1으로 돌아가 한 개의 community 를 찾을 때 까지 과정을 반복함
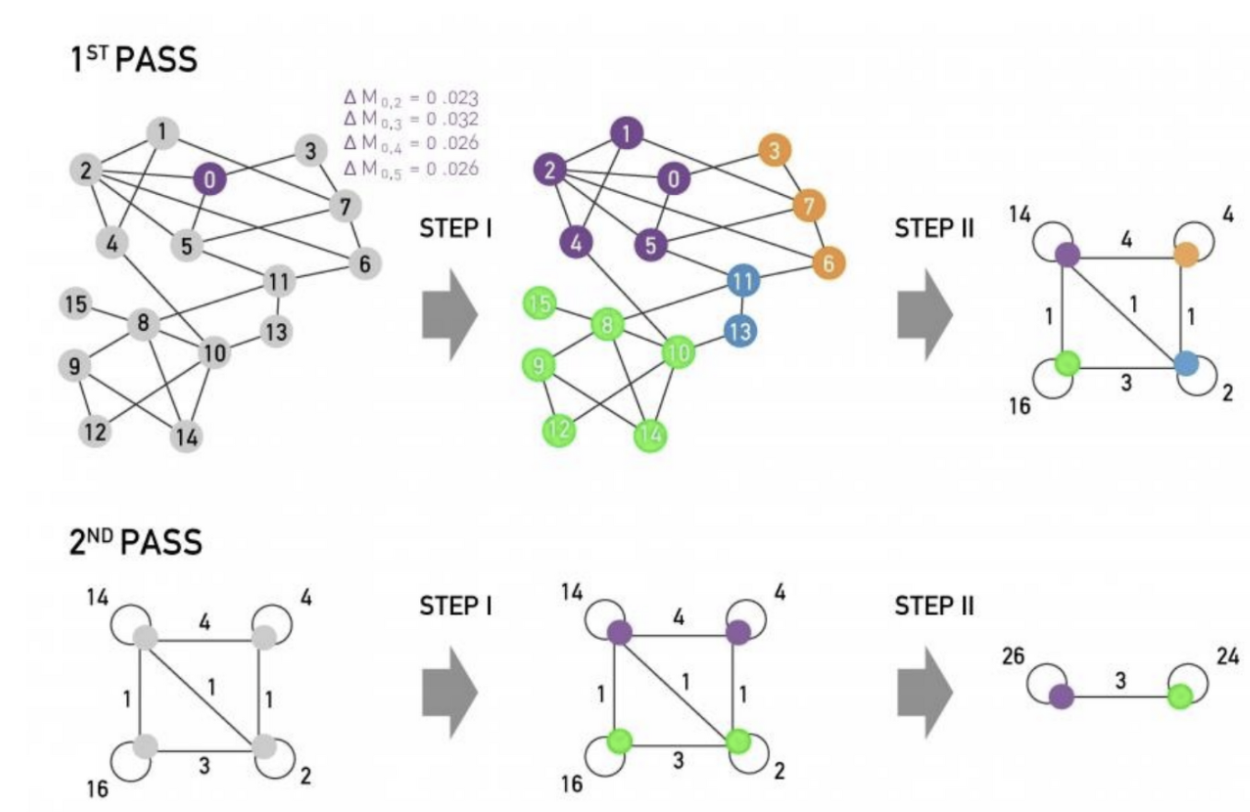
4. Dectecting Overlapping Communities : BigCLAM
- 실제 real world graph는 overlapping communities의 형태를 갖는 경우가 많다.
- Overlapping의 경우 인전행렬 또한 겹치는 부분이 존재
overlaps 알고리즘 설명
STEP1.
- Node community affilations에 근거해 graph를 위한 generative model 정의
- Community Affiliation Graph Model(AGM)
STEP2.
- Graph G가 AGM을 통해 만들어졌다는 가정을 가짐
- generated 된 G을 가지도록 최적의 AGM을 찾음 → AGM이 G을 generative 하도록 모델 파라미터 학습
- 위의 과정을 통해 커뮤니티를 찾을 수 있으며 각 파라미터는 노드가 커뮤니티에 얼마나 속하는 지 알려줌
Generative process
- model parameter :
- : community C의 노드가 각 노드와 연결될 확률
모델 파라미터(F)가 주어질 때, 그래프(G)가 생성될 확률을 구하고, 이 Likelihood을 최대화 하는 F를 찾음
- : 노드 u, v가 커뮤티티에 동시에 속할 확률
- MLE를 통해 를 최대화하는 F의 파라미터를 찾음
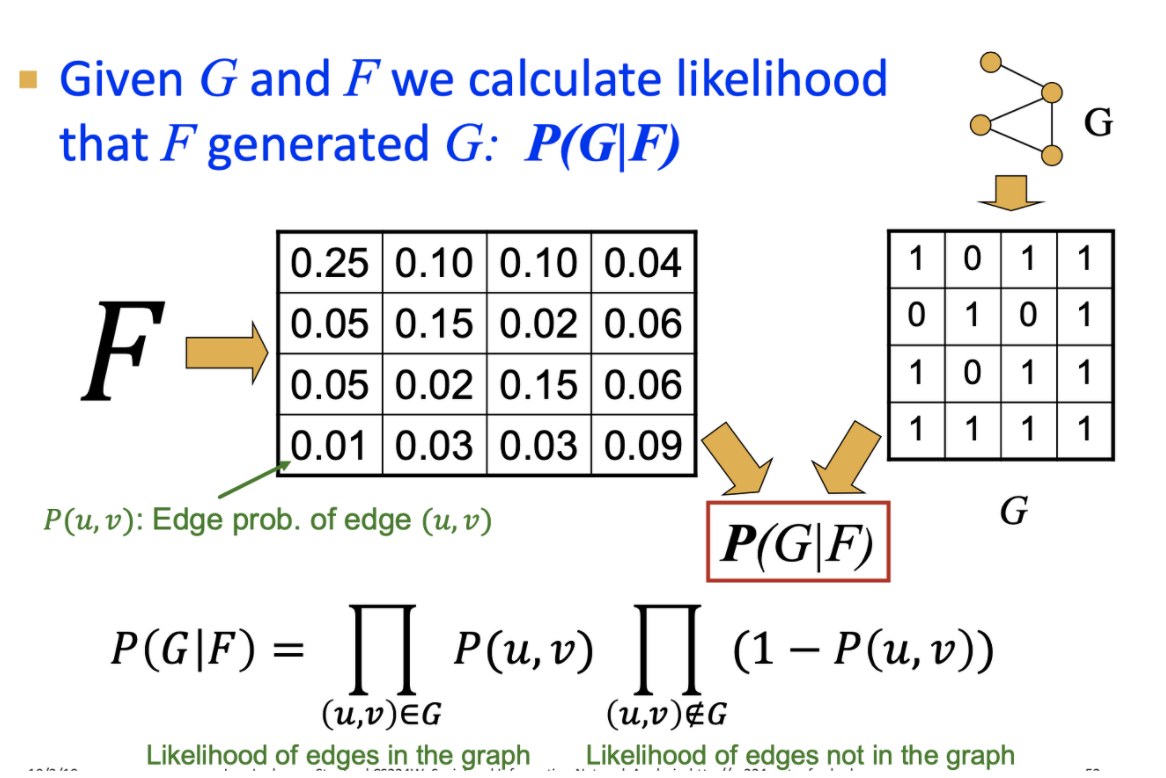
5. Spectral Clustering
Spectral Clustering의 개요
알고리즘은 3단계로 구성
1) Pre-processing
- 그래프를 표현하는 matrix 생성(Degree Matrix, Adejacency Matrix, Laplacian Matrix)
2) Decomposition(행렬 분해)
- matrix의 eigen value와 eigen vector를 계산
- 행렬을 eigen value와 eigen vector 기반으로 저차원으로 mapping
3) Grouping
- 행렬 분해를 통해 얻은 새로운 representation(eigen vector)로 2개 이상 Cluster를 만들고, 각 data point들을 Cluster에 할당
Partitioning 에 대한 용어 및 개념 설명
Graph Partitioning
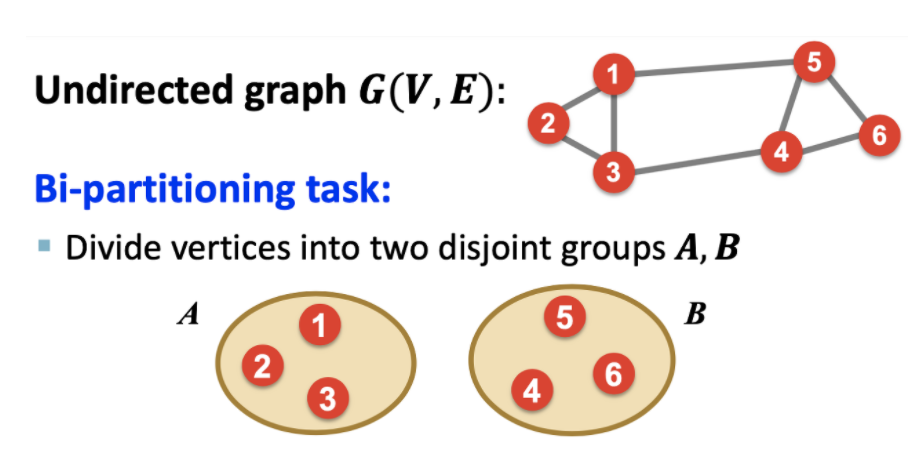
Q. 어떻게 그래프를 좋은 partition으로 나눌 것인가?
Q. 어떻게 효율적으로 partition을 정의할 것인가?
→ 그룹 내 노드간의 연결을 최대화 하면서 그룹 간 연결을 최소화 하는것이 좋은 Partitioning(일반 군집화 알고리즘의 클러스터링 평가와 일치하는 느낌)
Graph Cuts
- cut : set of edges with one endpoint in each
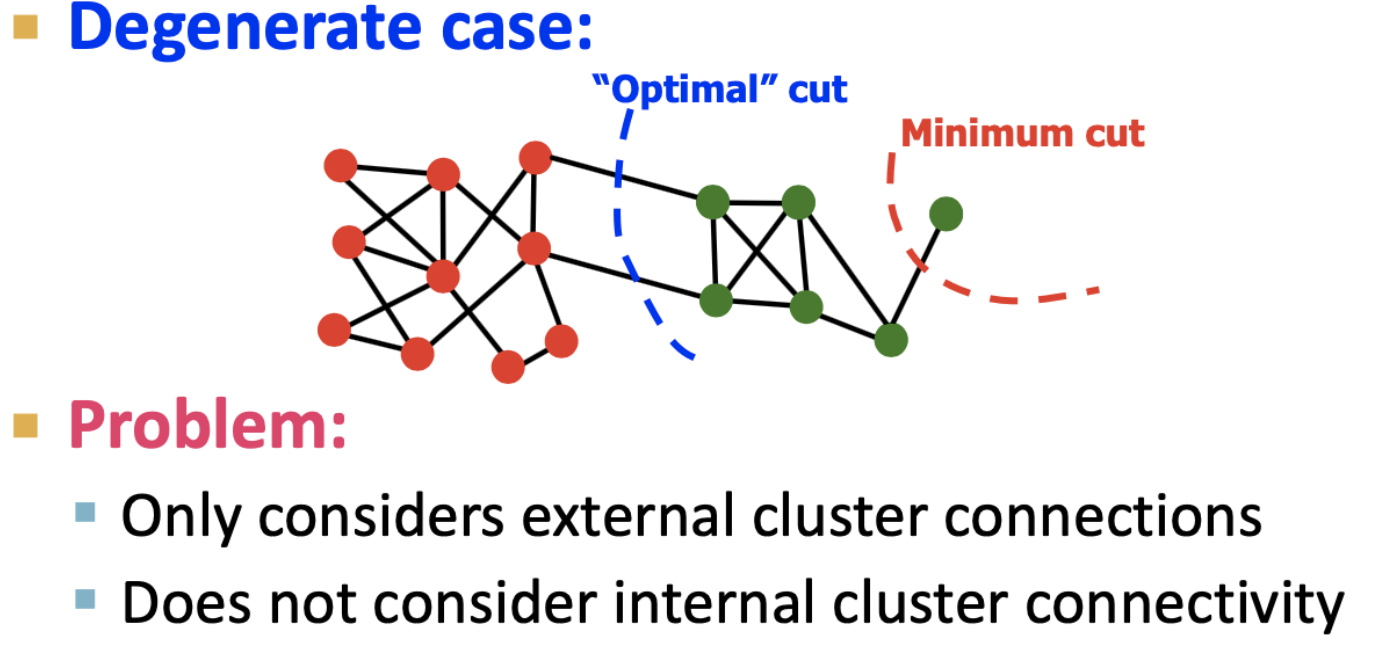
- minimum-cut
- 그룹들간의 연결 weight릃 최소화 함
- cluster 외부의 연결에만 집중하고, 내부의 연결성은 고려하지 않은 문제점이 있음 → Conductance를 고려하여 해결
- Conductance
- 군집 내부의 연결성을 고려(군집 내 Density를 반영)
- 각 그룹간의 Density는 상대적이므로 Cut을 각 그룹의 Volume으로 나눠 구함
- 따라서 더 균형을 갖춘 Partitioning을 할 수 있음
- 그러나, 최적의 Conductance를 찾는 문제는 NP-Hard
따라서 Conductance를 구하는 과정에서 eigenvalue와 eigenvector를 이용하는 방법을 선택하는 것
Spectral Graph Partitioning
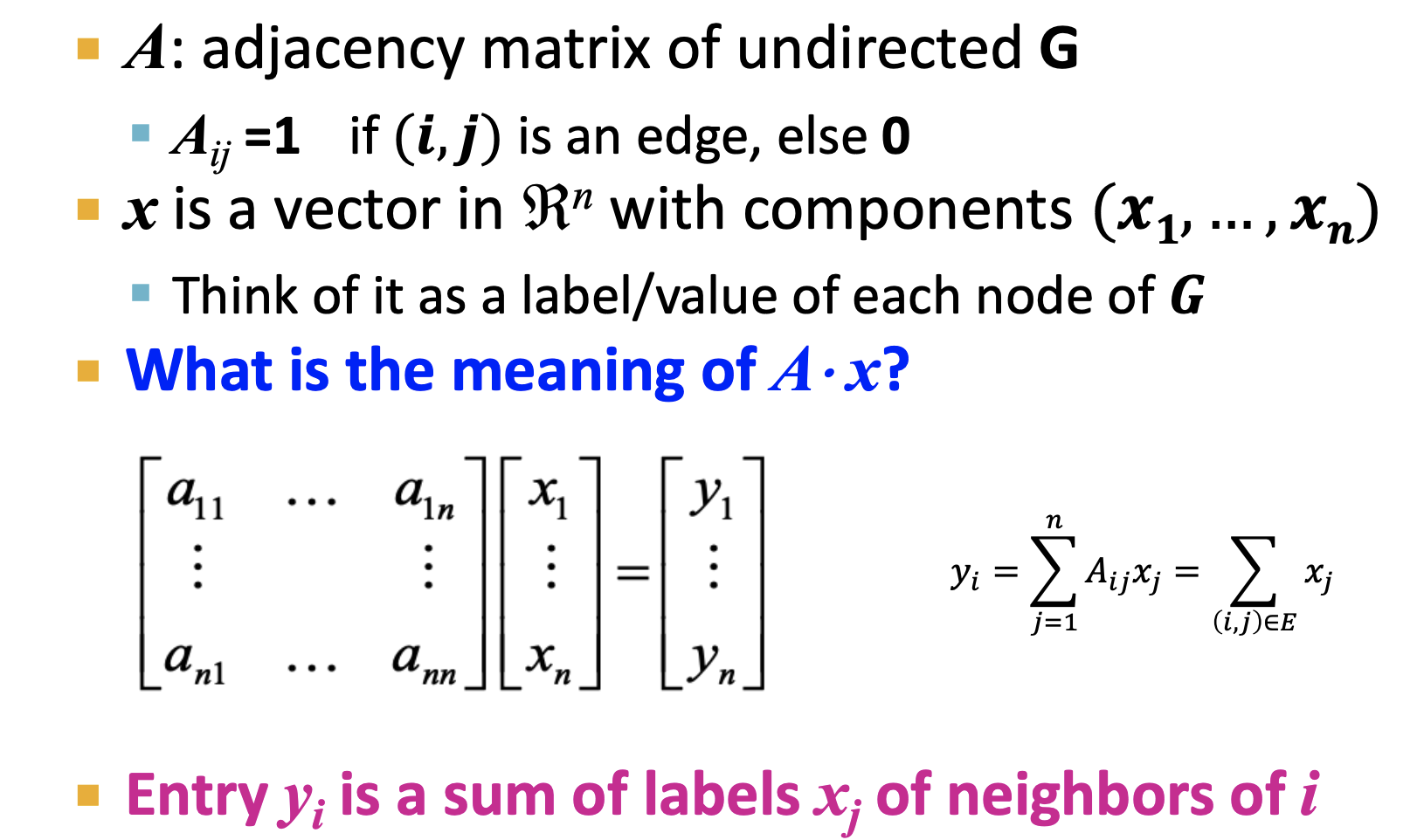
Q. A * X 의 의미?
- A * X의 선형변환은 노드 i의 이웃인 j의 라벨들의 합
Spectral Graph Theory는 Matrix Representing G의 Spectrum을 분석하는 방법
- spectrum : 그래프의 eigenvector 는 eigen value 의 크기 순으로 정렬한 것
예시) d-regular graph(모든 노드가 동일 degree를 가진 그래프)
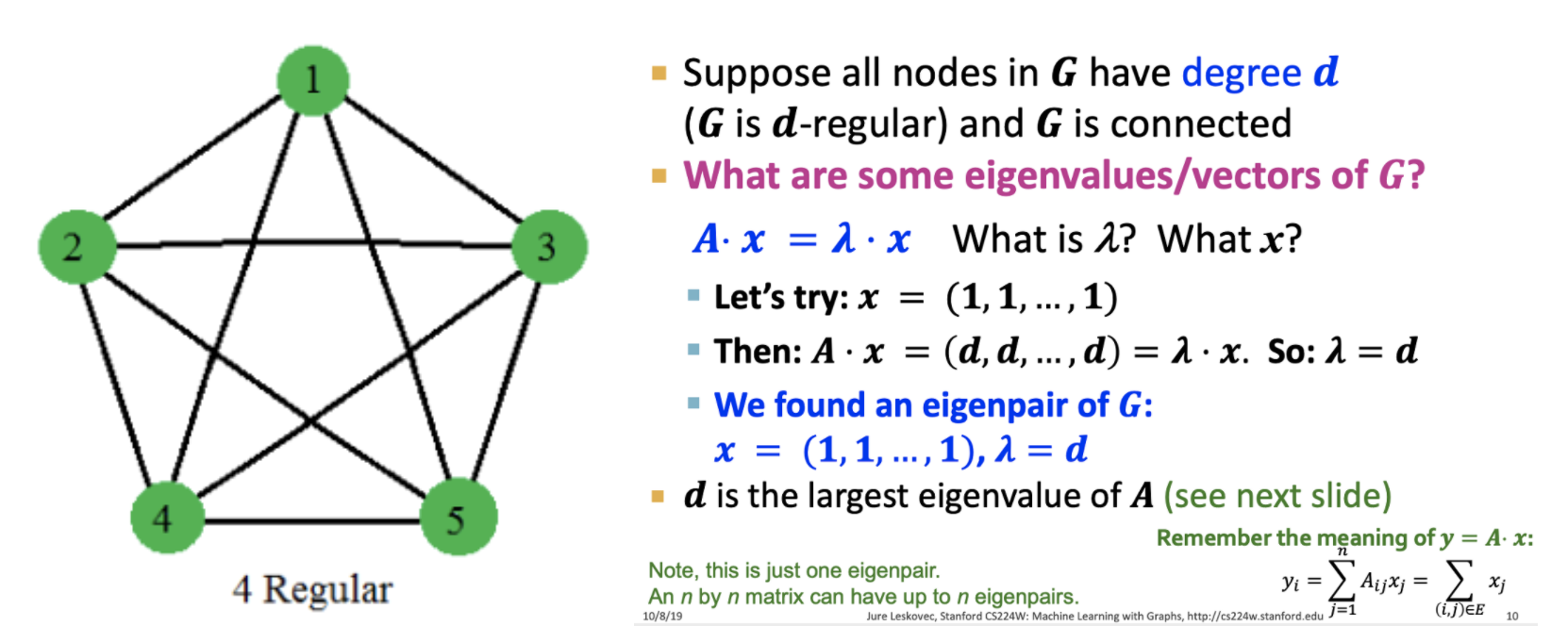
Q. 에서 와 는 무엇인가?
- 를 (1, 1, ... , 1) 벡터라 하자.
- 그러면 이 되고 가 됨
- 는 의 가장 큰 eigen value이며, 가 n by n 행렬일 때, n개의 eigen vecor, value가 나오게 됨
Matrix Representations
- Degree matrix
- Adjacency matrix
- Lapacian matrix
- eigen value가 음이 아닌 상수
- eigen vector가 항상 orthogonal

Q. 의 의미?
- 와 의 차이를 제곱한 값의 합
(증명 생략)
는 균형있게 파티셔닝 하기 위해 찾은 eigen value
→ 최적의 cut을 찾는 문제는 두 노드간의 차이를 최소화 하는 를 찾는 문제로 바뀌게 됨

정리하면 를 최소화하는 것이 최적 Cut을 찾는 일임
이는 Laplacian Matrix L의 를 찾는 것과 같음
즉, 를 만족하는 벡터 는 eigen vector 임
→ 와 eigen vector를 이용한 클러스터링이 conductance(cut criterion)을 최소화 하는 것을 입증한다 함
알고리즘 요약
Q. 어떻게 그래프의 좋은 Partitioning을 정의 할까?
→ 주어진 그래프의 cut criterion을 최소화
Q. 어떻게 Partitioning의 효율적인 구분이 가능할까?
→ 그래프의 eigen value와 eigen vector를 구해 근사정보를 활용한다
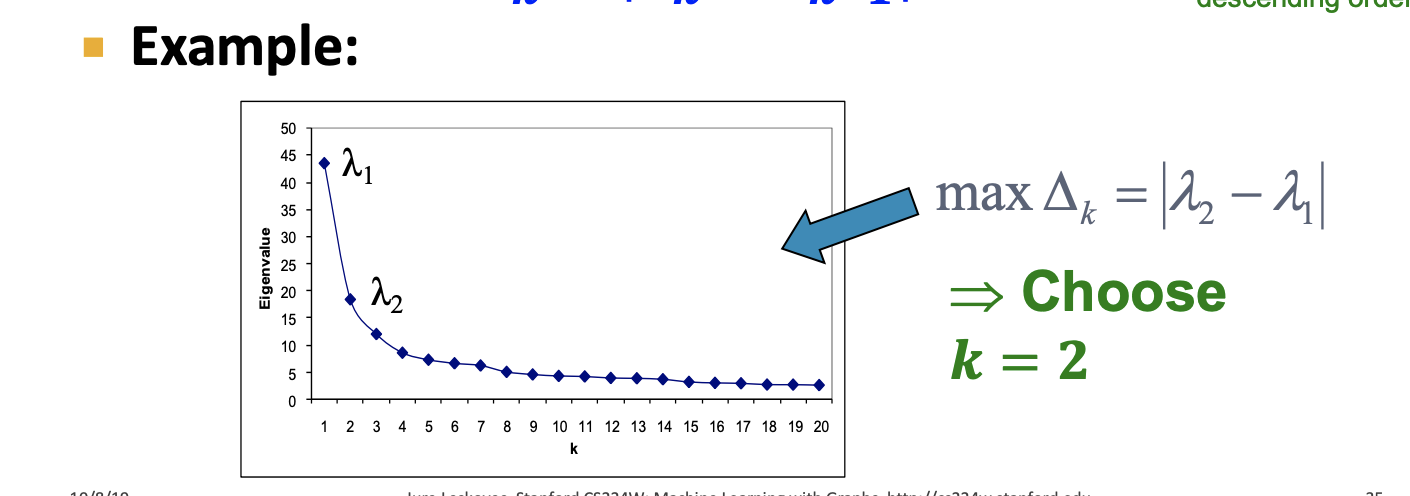
최적의 K를 찾는 것은 딱히 최적의 방법은 없고 eigen gap을 최대화 하는 지점을 찾는다함(elbow point 느낌)
Eigen gap : 두 연속적인 eigen value의 차이
Motif-based Spectral Clustering
- motif 기반의 Spectral clustering 알고리즘
- motif : recurring, significant patterns of interconnections
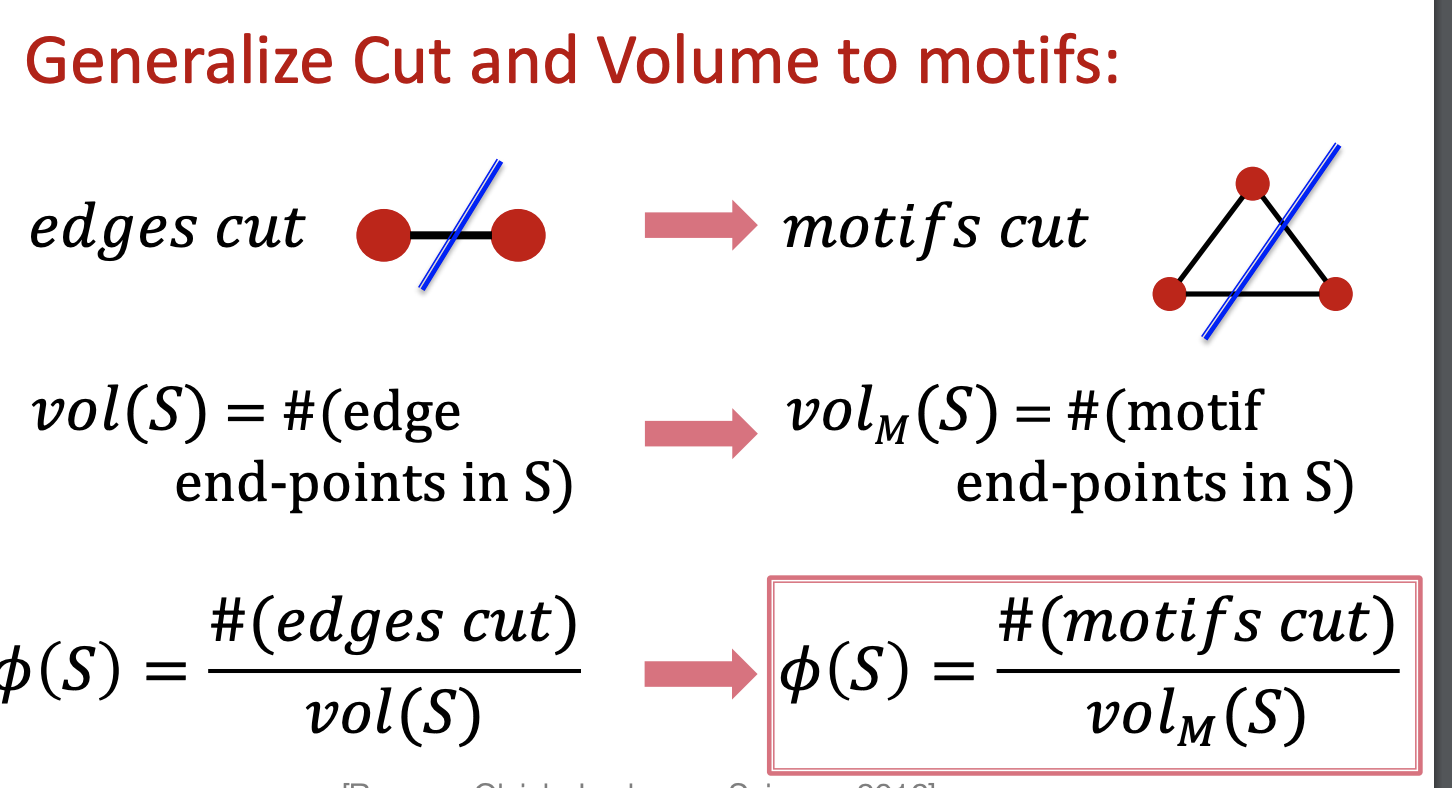
motif의 Conductance를 찾는 것 또한 NP-Hard 문제
알고리즘
- 주어진 그래프 G에서 motif M이 나타나는 edge의 갯수로 wighted graph W를 만듬
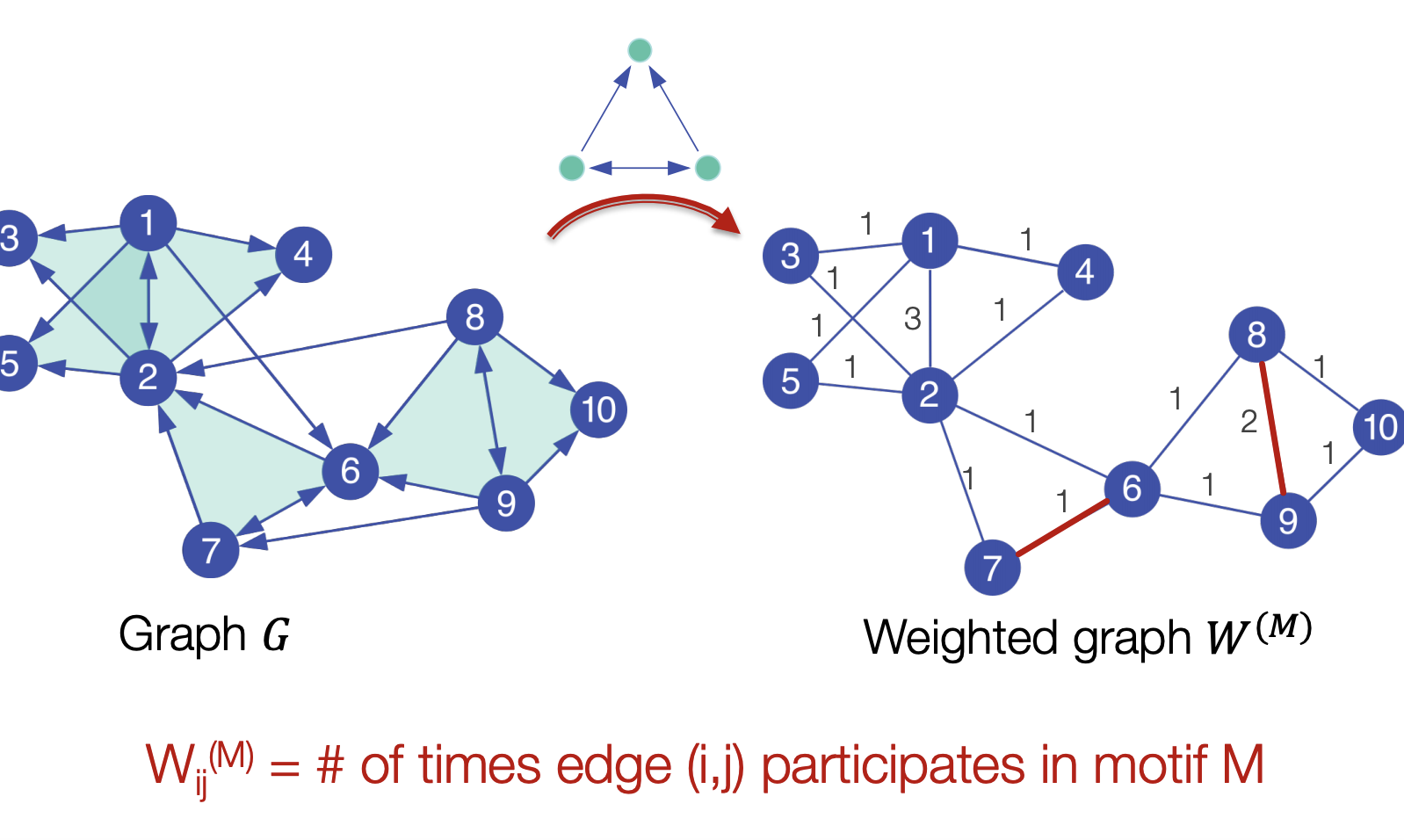
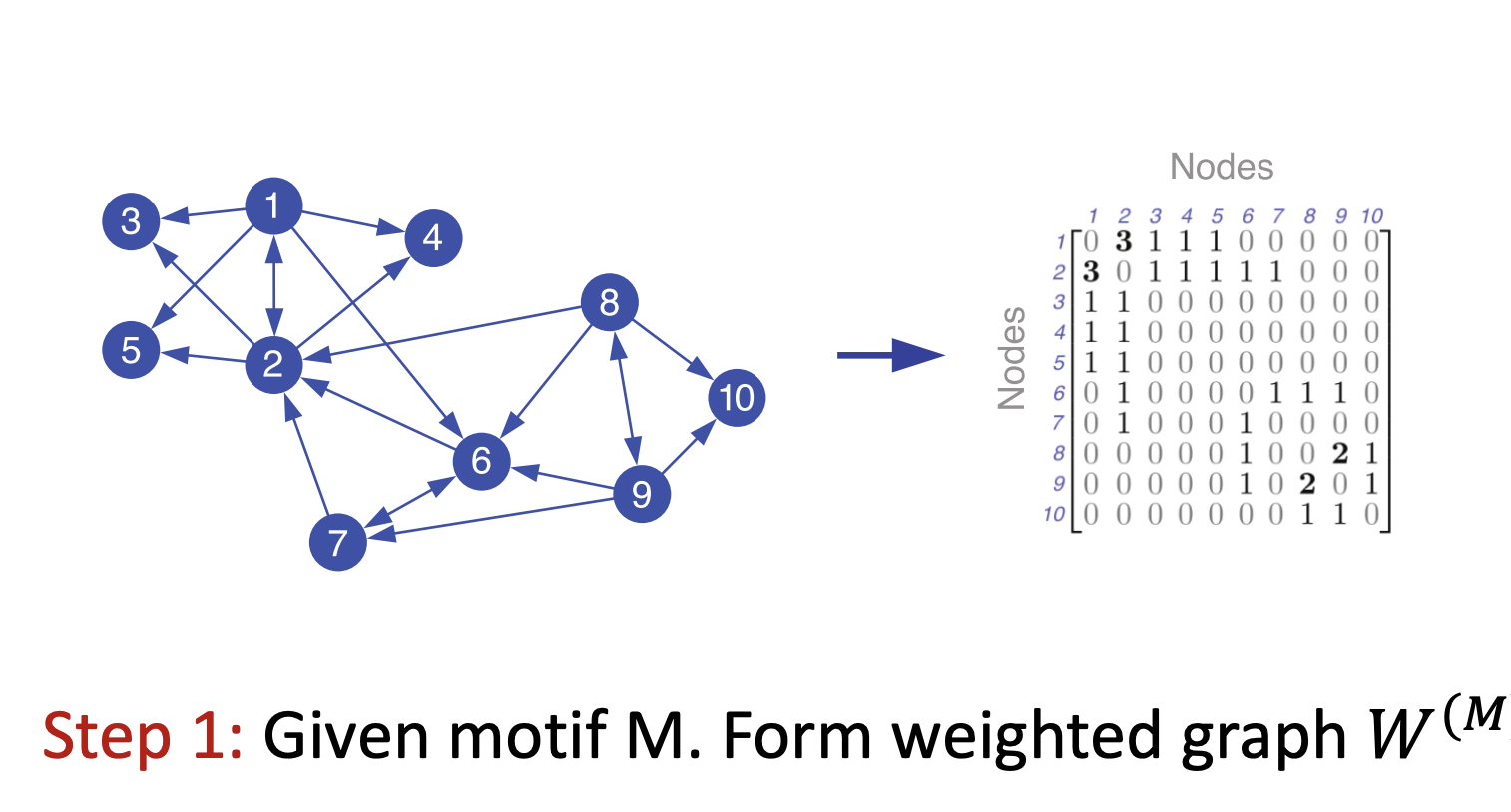
- 에 대해 Laplacian Matrix를 구하고 eigen vector와 eigen value를 구함( 를 구하는 것이 목표)

- 값을 정렬하고 x축을 각 S집합, y축을 Conductance하는 plot을 그림. Conductance가 최소화 되는 지점은 휴리스틱하게 찾음
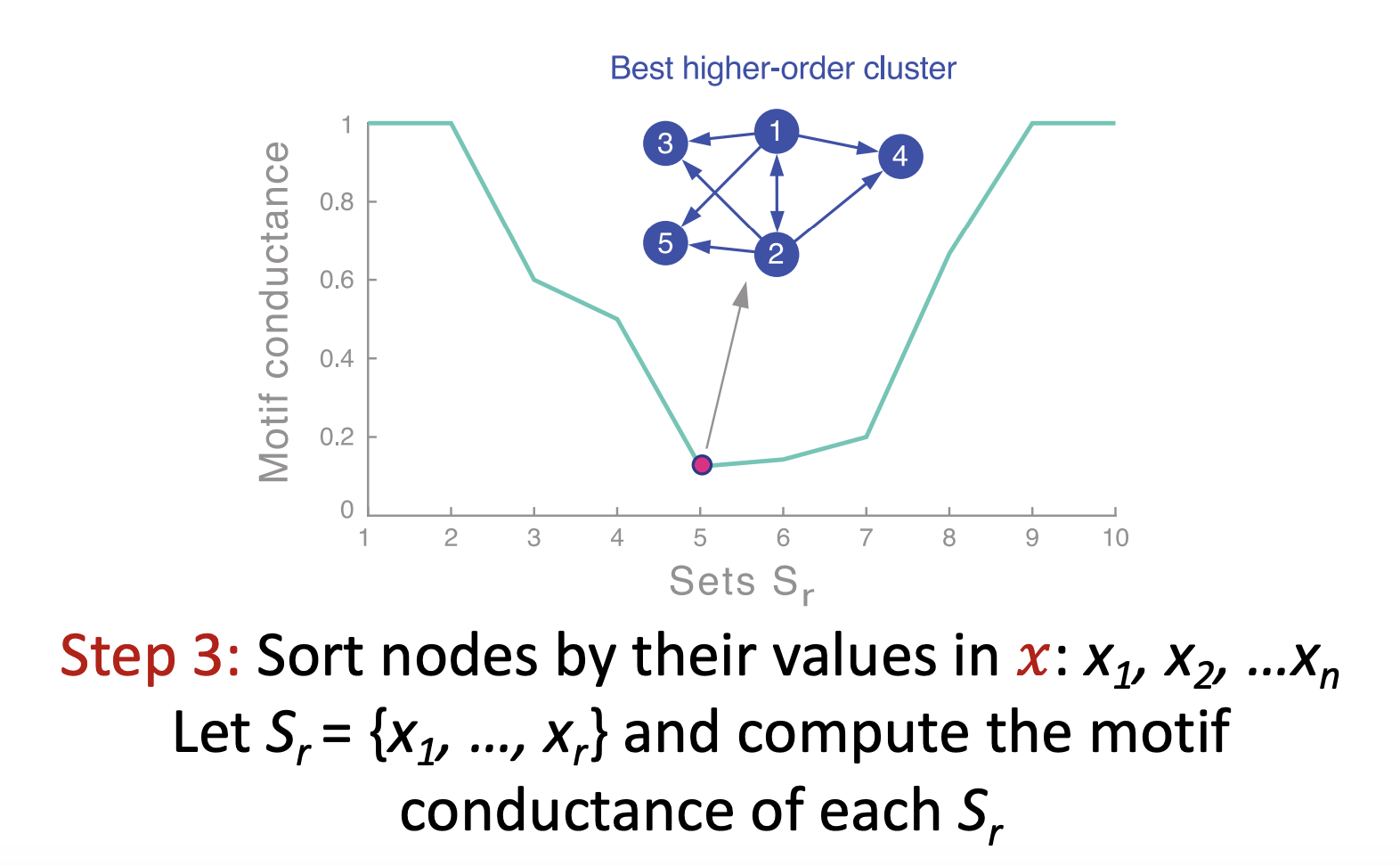
- 알고리즘의 결과는 아래의 수식이 보장된다 함. 알고리즘을 통해 찾은 conductance값이 거의 최적 값에 가까움(near optimal)

Reference
CS224W: Machine Learning with Graphs
