CS224W의 Limitations of GNN, Advanced topic in GNN, A General perspective on GNN, Scaling up GNN Large Graph 강의 중 GNN의 한계점과 대안법에 요약한 글
1. Graph Isomorphism을 구분하는 문제

→ agg 과정에서 max pooling이나 mean pooling을 하게 되면, 두 그래프는 같은 결과 값이 나오게 됨
→ 이를 해결하기 위해, Injective function을 agg function으로 사용
injective function : 하나의 Output에 하나의 원소를 mapping하는 함수
→ node의 subtree가 다르면 representation이 달라지게 됨
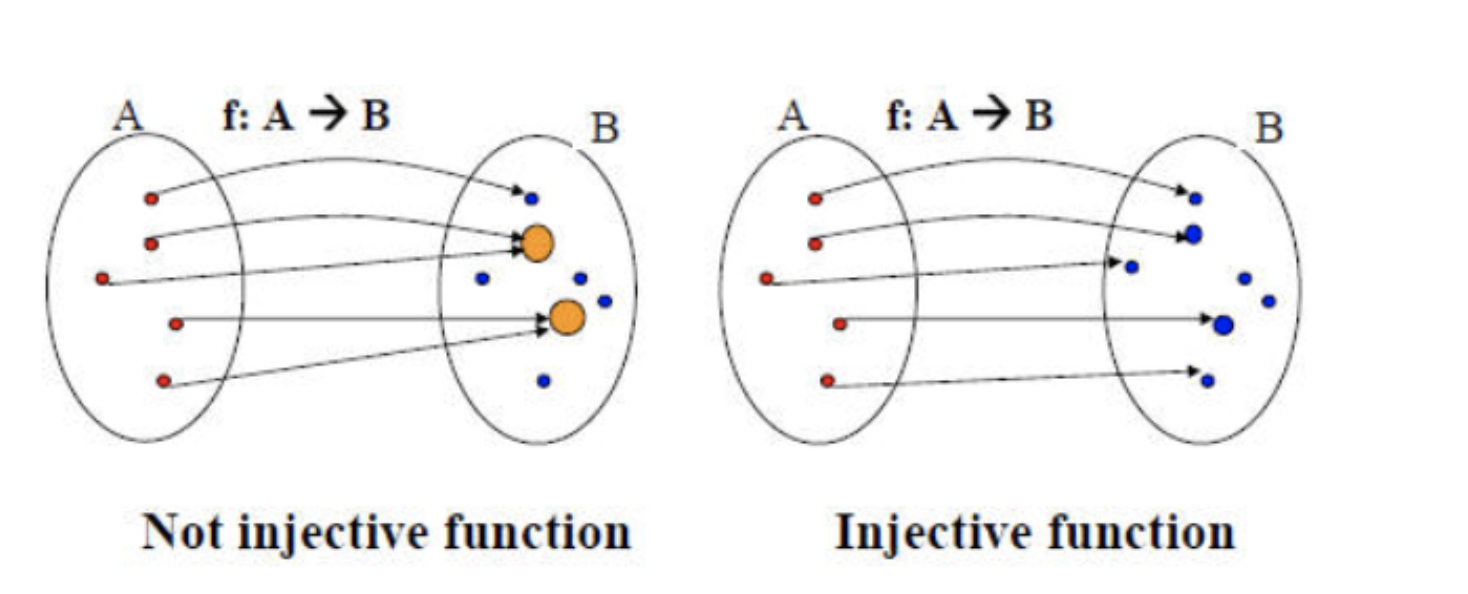
즉, Injective function을 통해 동형 그래프라도 각 Node의 subtree가 다르면, node representation을 다르게 가져가겠다는 것.
예시 1) GCN의 Not injective 예시
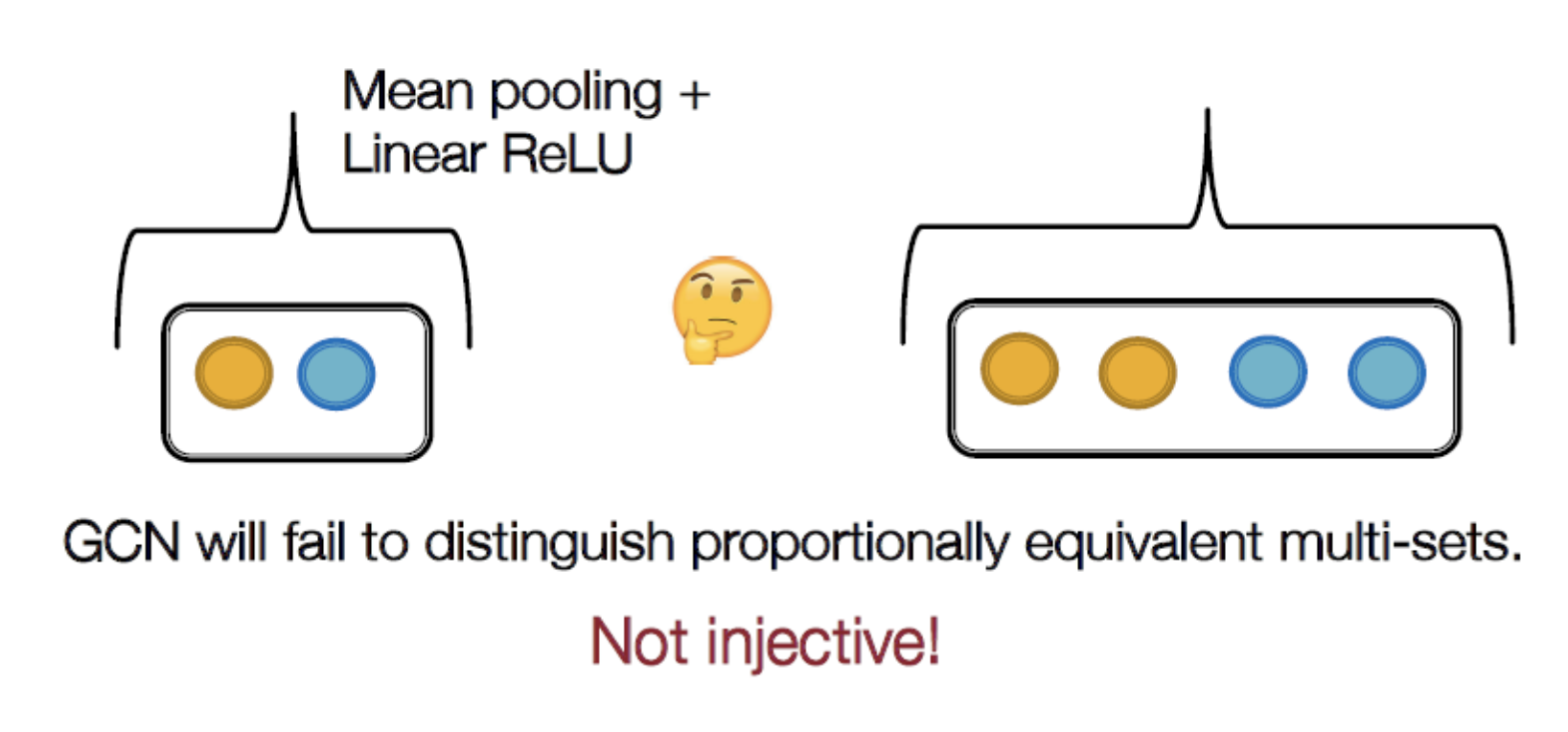
→ GCN은 multi-set을 적용하더라도 injective 하지 않음(mean pooling을 하기 때문)
예시2) GraphSAGE의 Not injective 예시
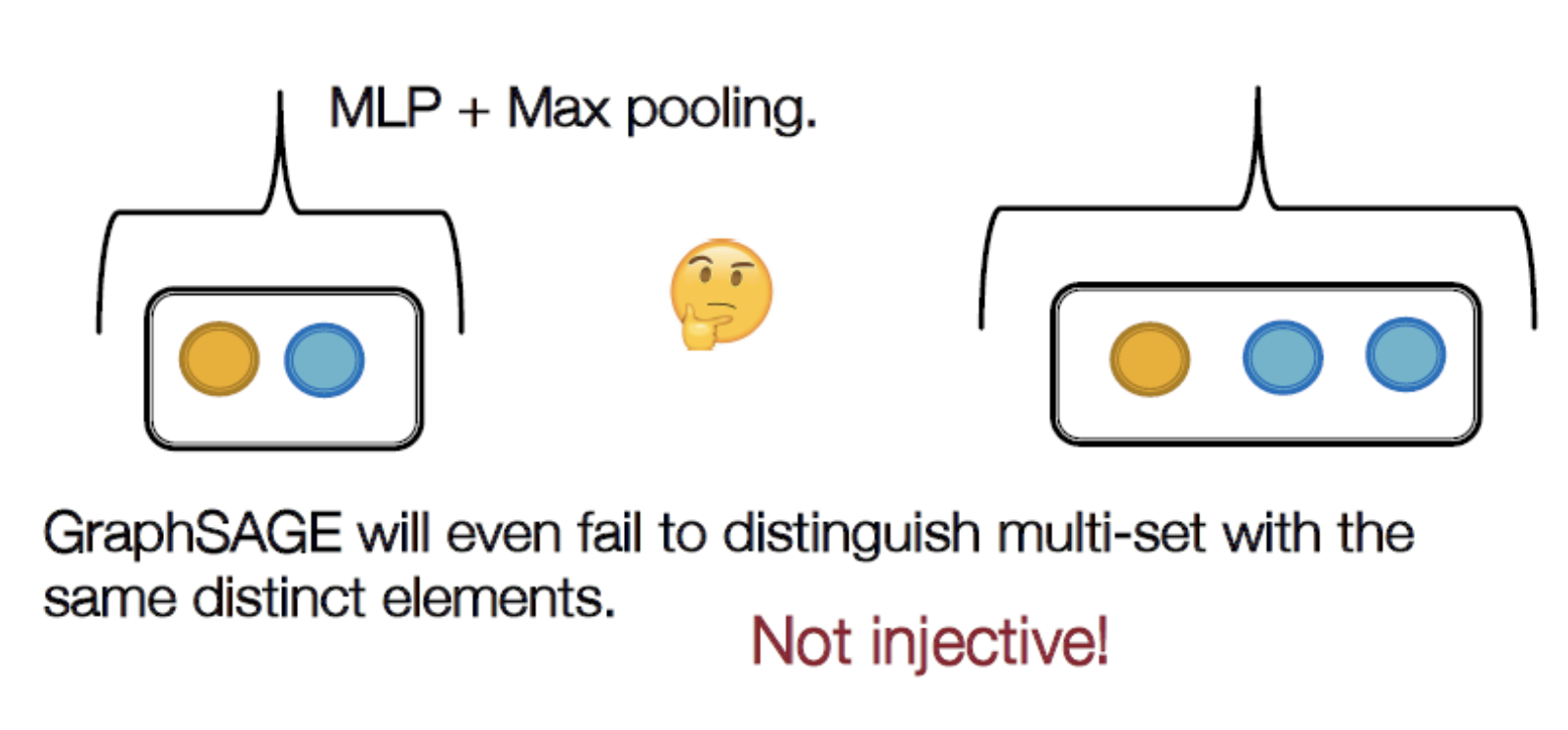
→ max pooling이기 때문에 노드 개수가 의미 X
- Injective Multi-set function
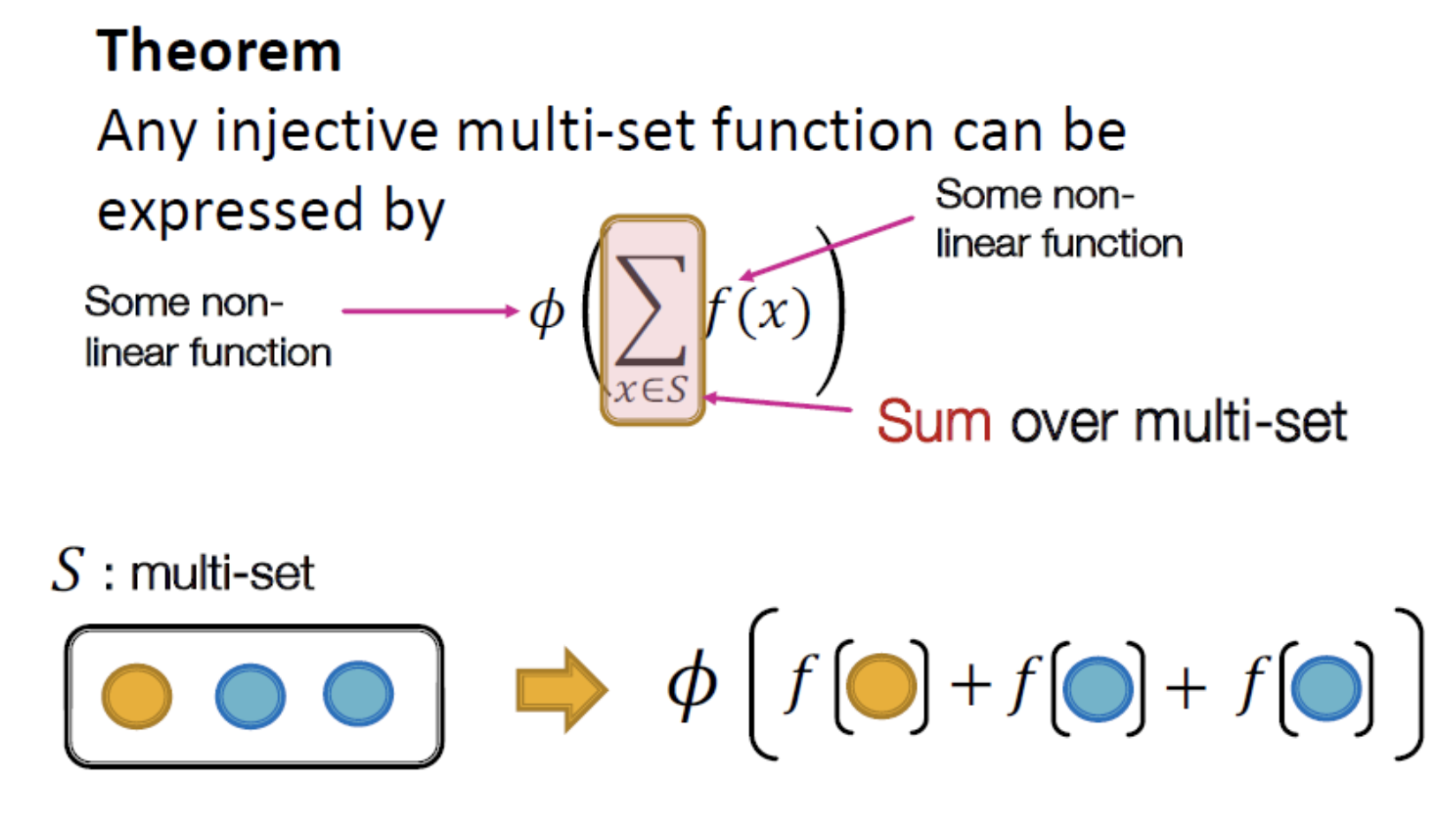
Graph Isomorphism Network(GIN)
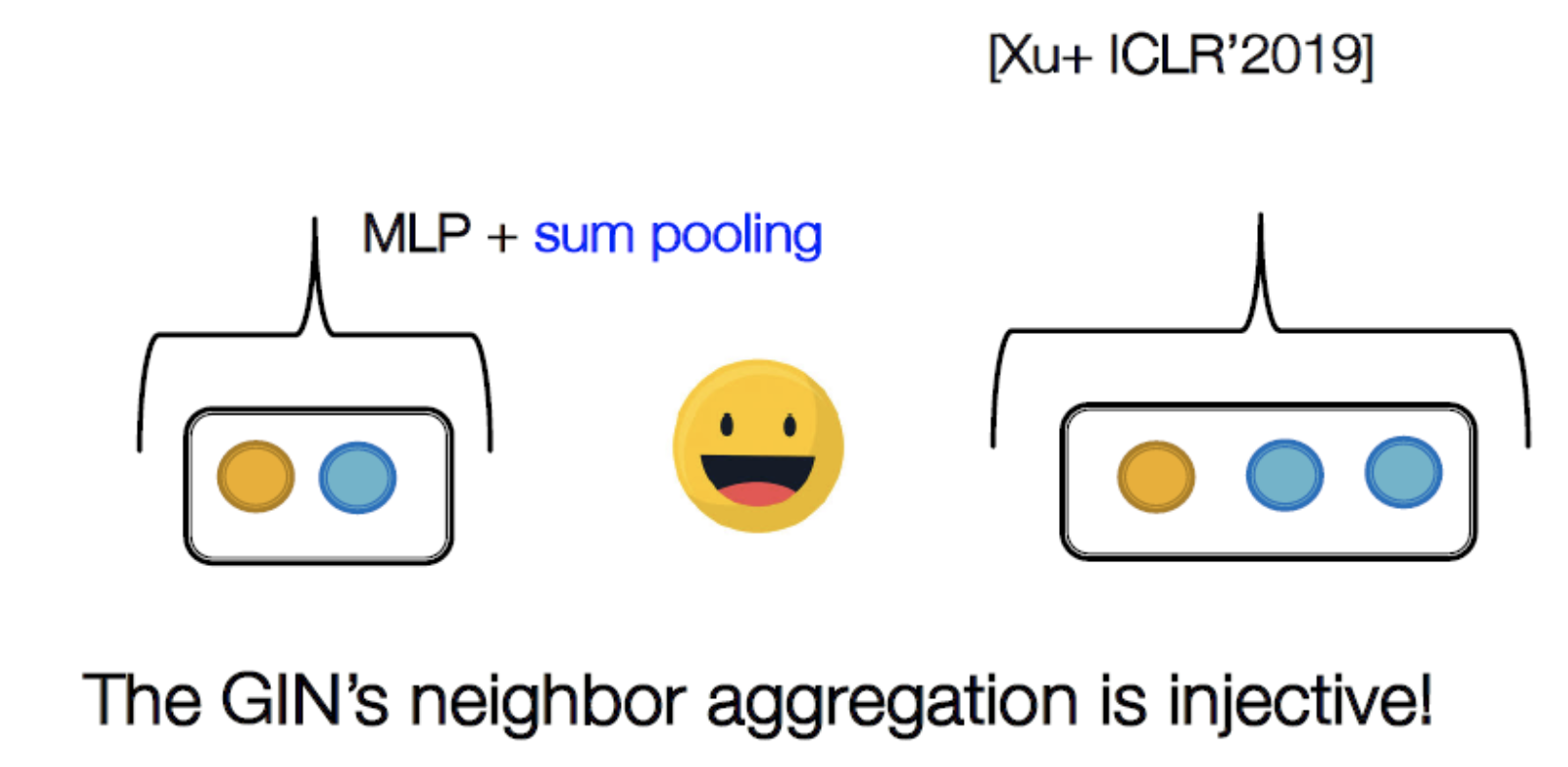
→ root에서 sub tree를 내리고 node의 색을 부여해 구분. 이를 통해 동형그래프를 판단. 개수만으로 결정 하는 것이기 때문에 node feature가 존재할 경우에는 큰 의미 없다?
- GIN의 Computation 예시. 아래 방식을 Weisflier-Lehman(WL) Graph Isomorphism Test라 함 → subtree 확인 후 동형그래프면 같은색 아니면 다른 색 부여함
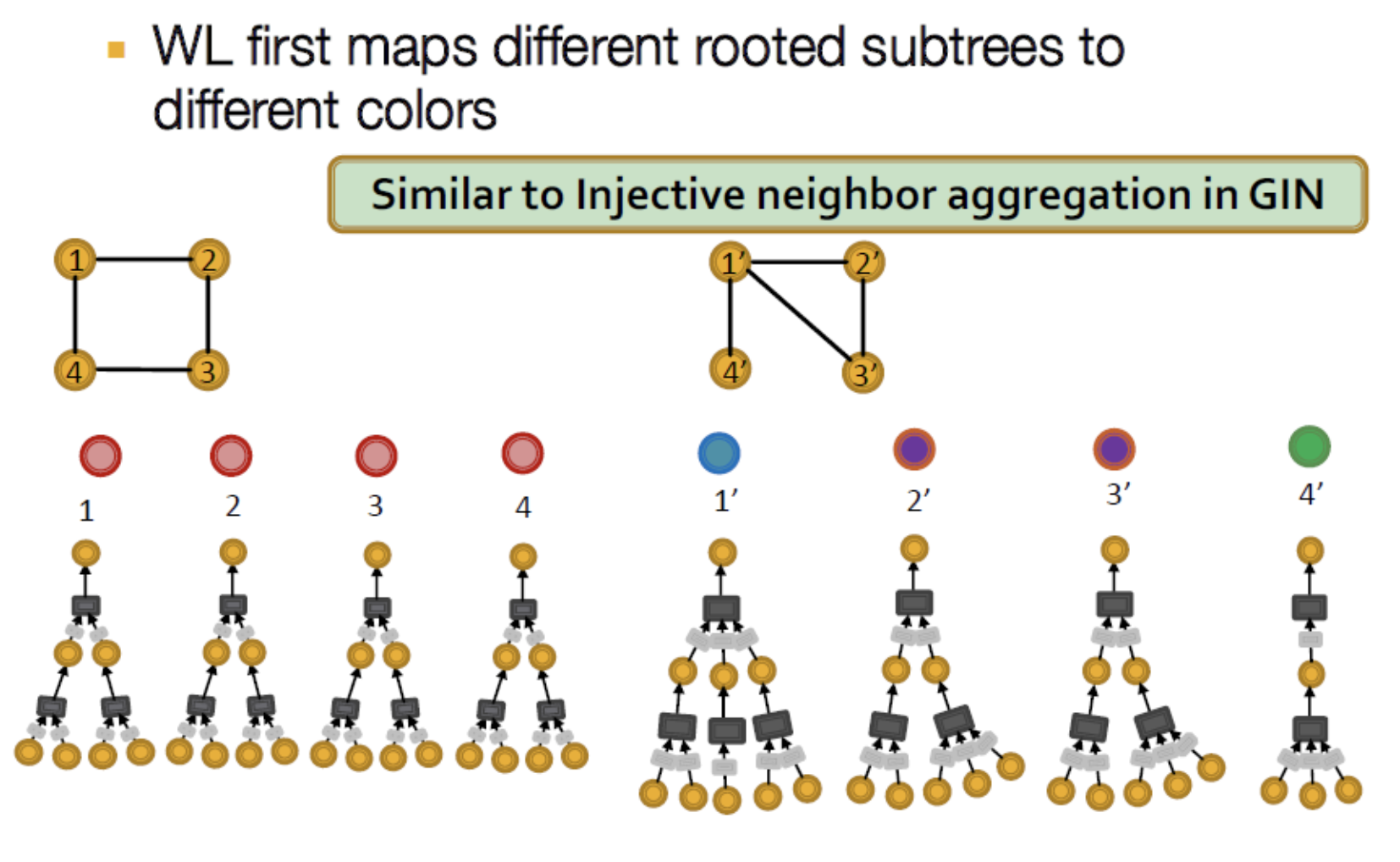
- 그러나 모든 node가 같은 수의 subtree를 가진다면 WL로 구분 불가.
- 여러 task에서 SOTA성능을 보였다하며, node feature가 주어지면 타 알고리즘과 큰 차이가 없다.
2. Vulnrability of GNNs to noise ingraph data
- GNN은 그래프의 노이즈(node feature의 변화, edge 추가/삭제)에 robust 하지 못함
- Direct attack : target node의 feature/connection 변경
- Indirect attack : target node의 neighborhood feature/connection 변경
기타 한계 사항으로는 라벨링 데이터 부족, 실제 학습과 테스트의 분포가 다른 이슈가 있다함
3. Node의 Identift aware 문제
문제 1. 같은 이웃구조 → 같은 노드 임베딩 가져야 함 → position aware 문제
문제 2. 다른 이웃구조 가지면 다른 노드임베딩 가져야함
→ Cycle의 length를 고려하지 못하는 문제
즉, Node의 Identify aware task를 말하는 주제
문제 1에 대한 예시
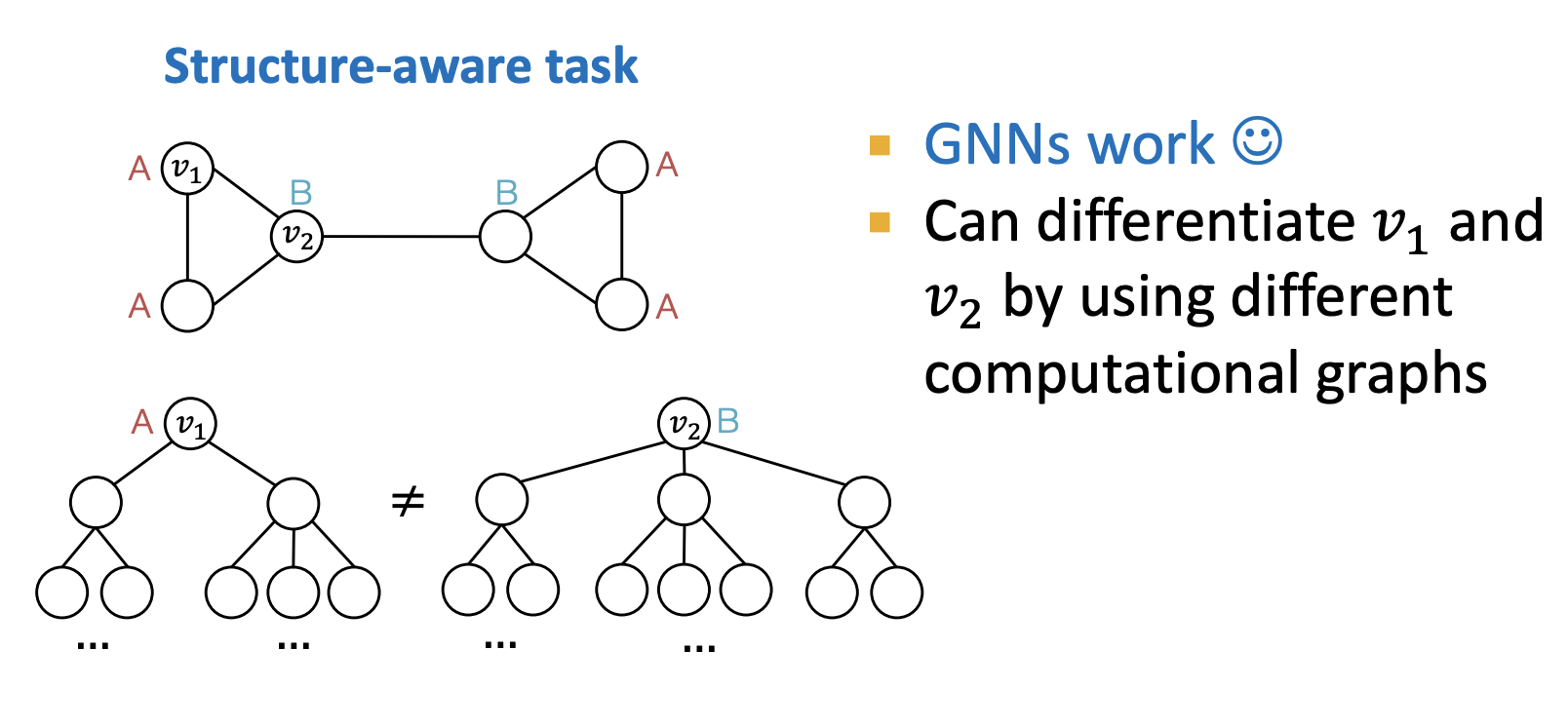
- 노드 v1와 v2의 Computational Graph는 다름
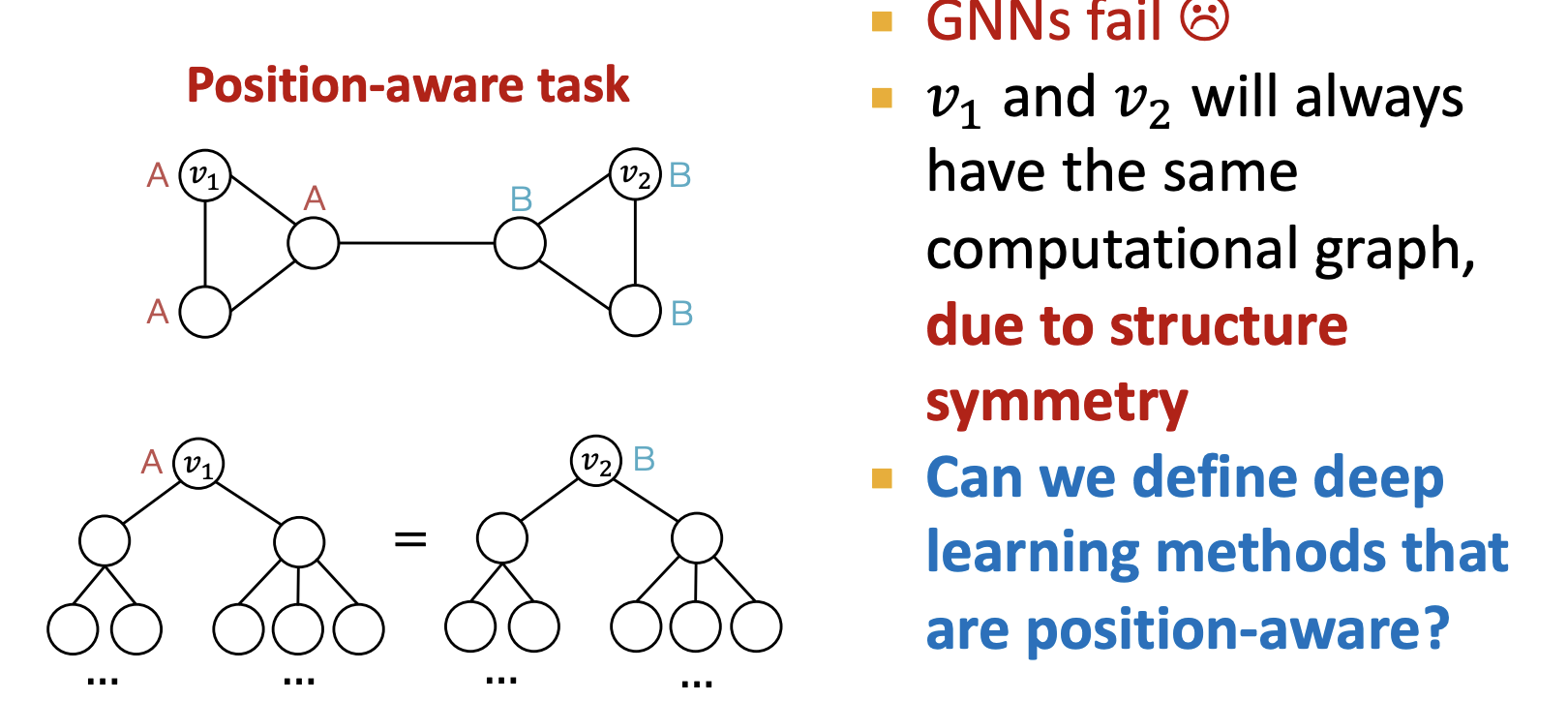
- 노드 v1와 v2의 Computational graph가 같음 → 해결방법? Anchor node를 이용
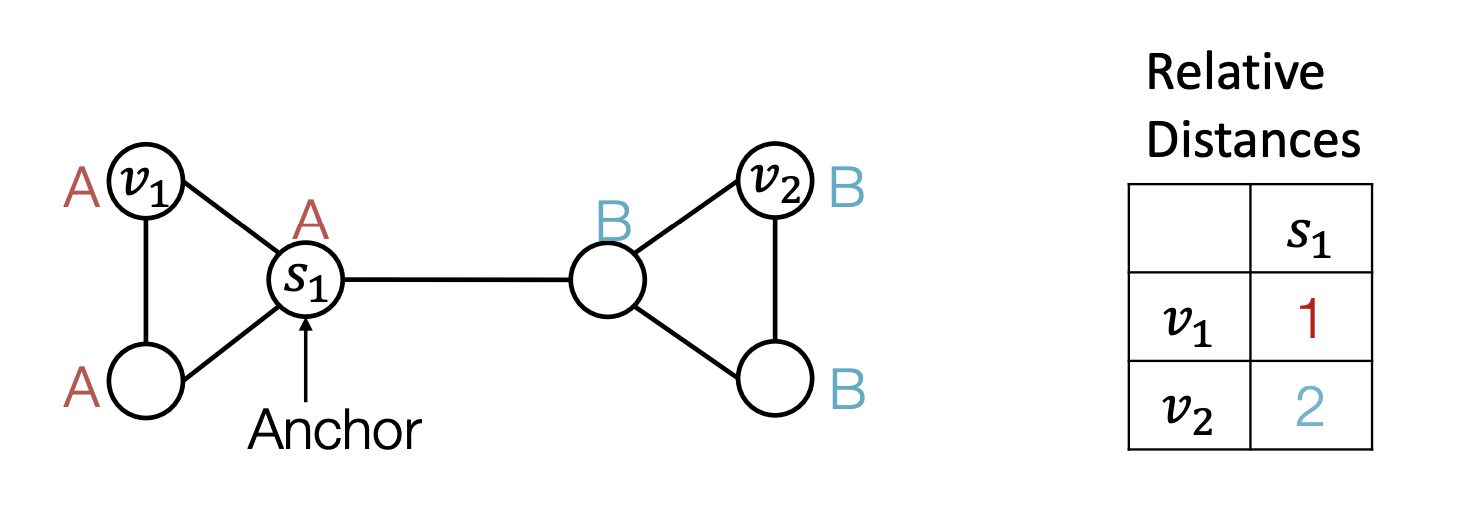
- s1를 ahchor node로 고려한다면 relative distance를 계산할 수 있음
- 많은 anchor set은 더 정교한 position 정보를 줄 수 있음
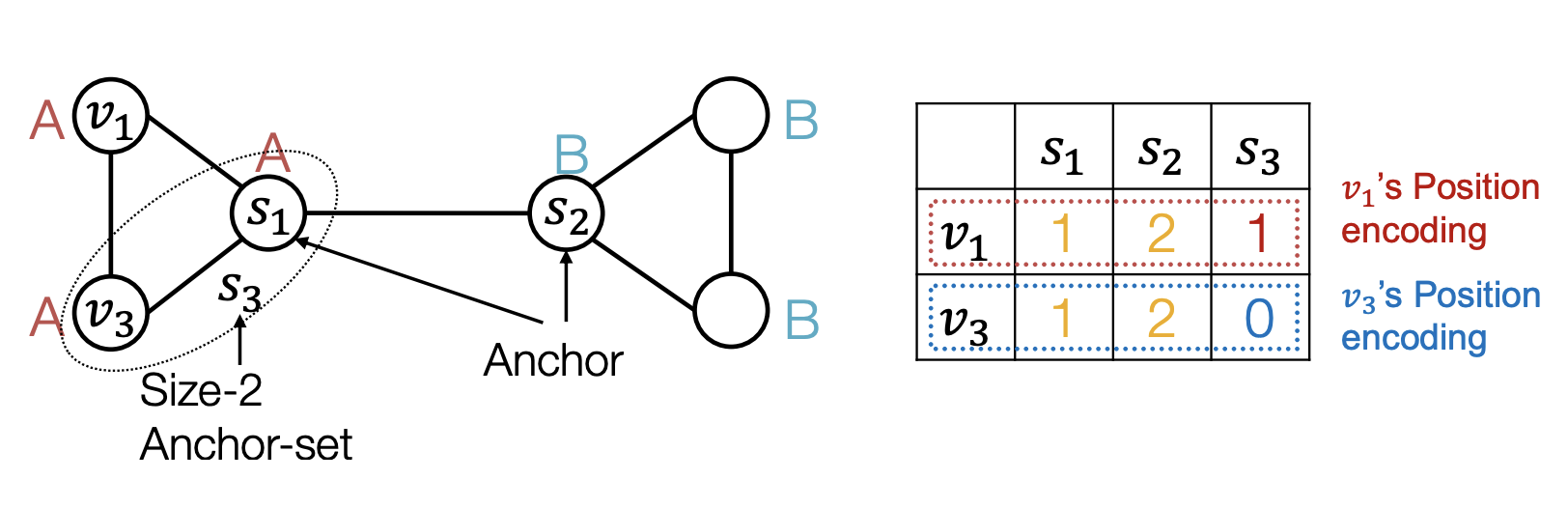
Q. GNN은 structure-aware task에서 완벽히 작동? NO!
- Node level, Edge level, Graph level 에서 실패 케이스가 있음
같은 Computational graph 를 가져 structure aware 에 실패한 사례
1) 사례(Node level)
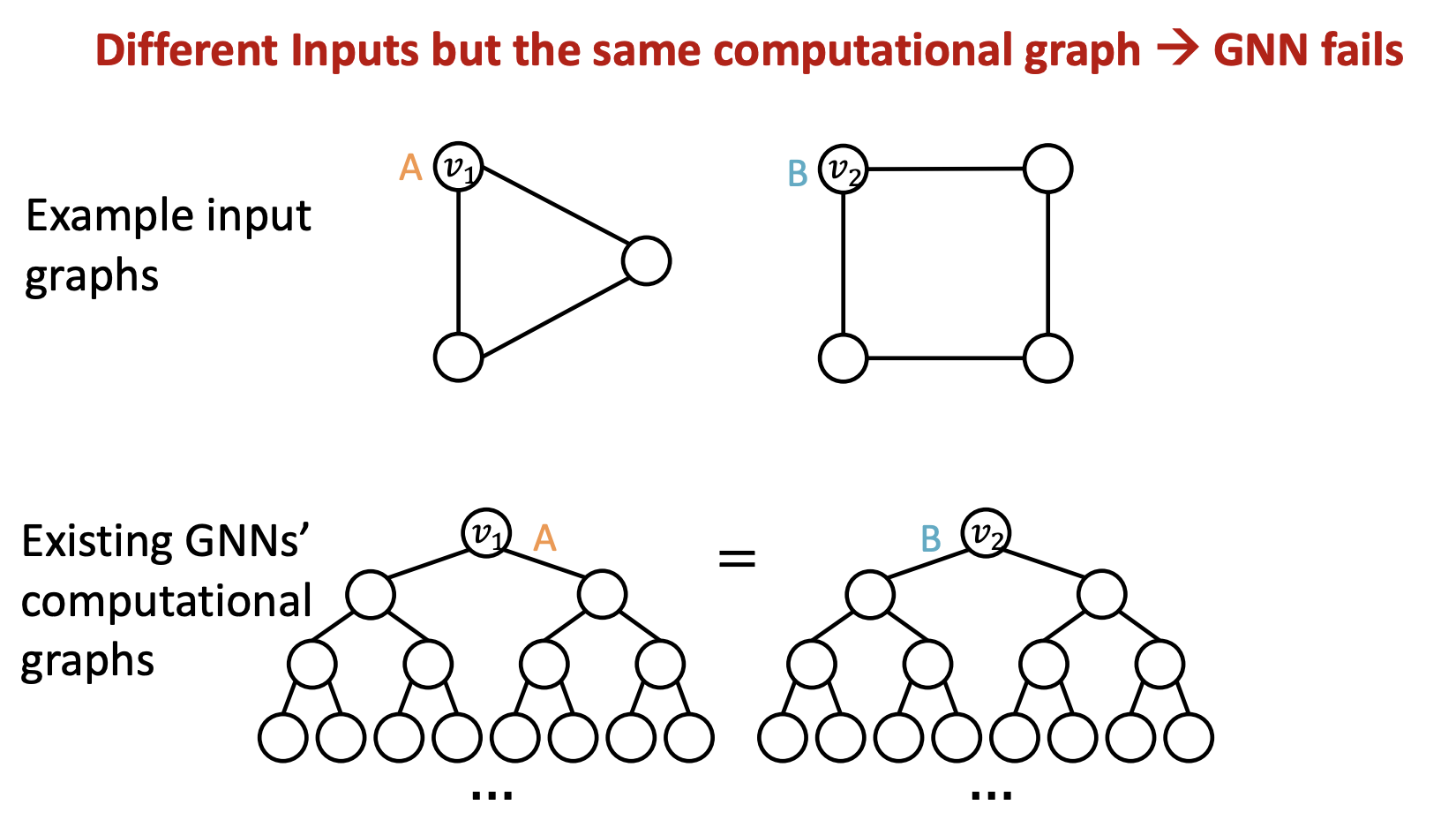
2) 사례(Edge level)

3) 사례(Graph level)
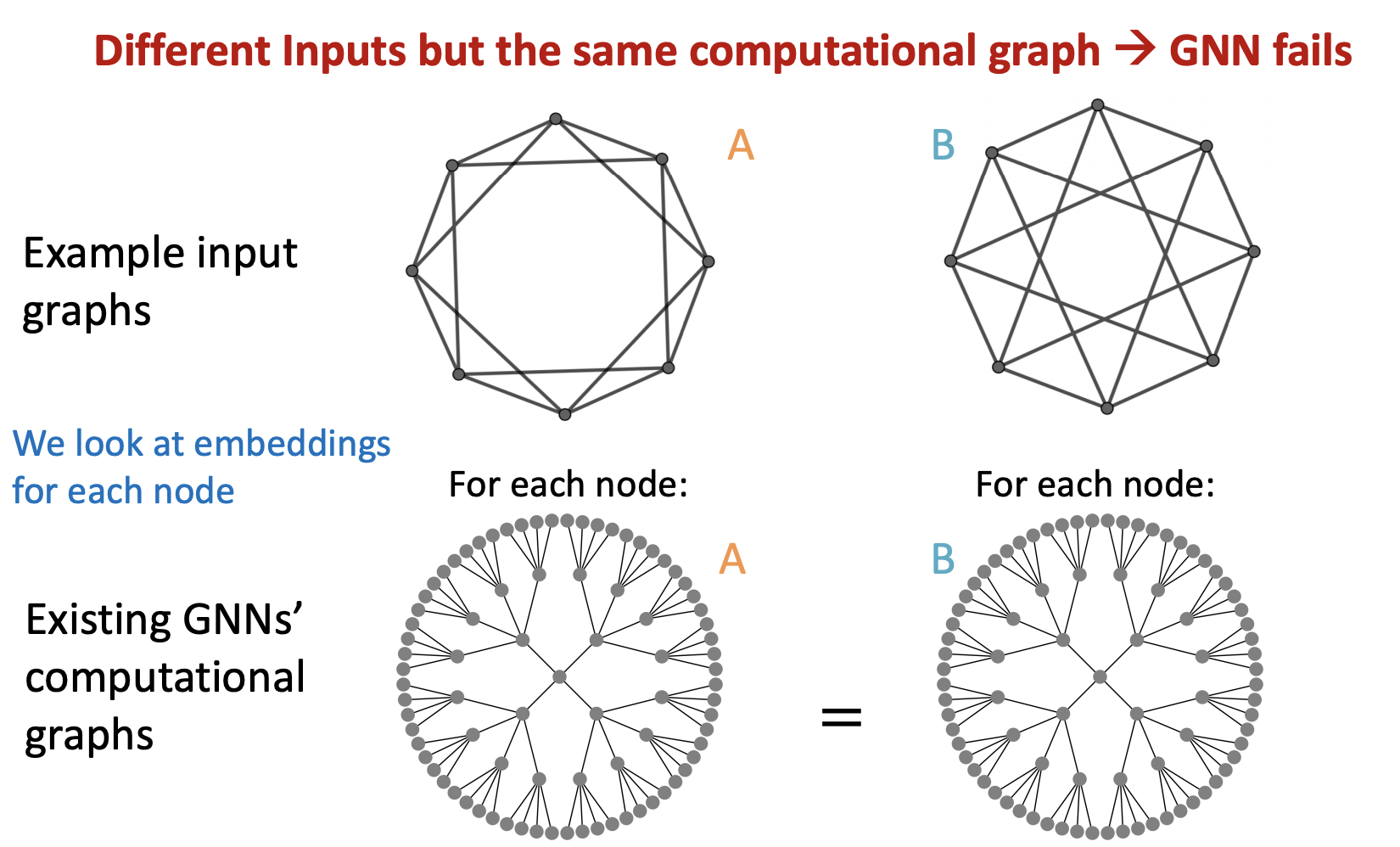
- Inductive Node Coloring을 이용해 structure-aware 문제 해결

- node level사례 외에도 graph, edge level 문제도 해결
Q. 그럼 node coloring 을 사용한 GNN을 어떻게 구축?
→ Heterogenous message passing을 사용(color에 따라)
(vanilla GNN의 경우 하나의 message passing을 사용)
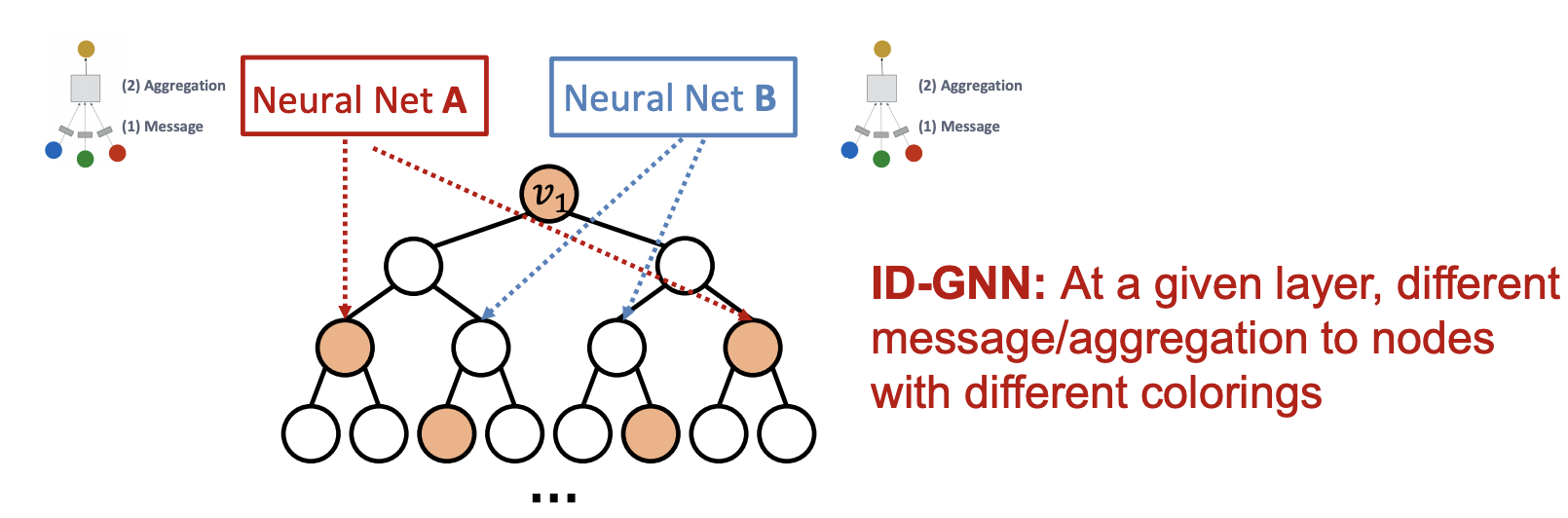
Q. ID-GNN이 Vanilla GNN보다 나은점?
→ 주어진 노드에서 Cycle length가 고려된 임베딩이 가능해짐
→ 좀 더 심플 버전 ID-GNN의 경우, augmented node feature를 사용해(이걸 Cycle count에 사용한다 함) heterogenous message passing 이 필요 없고 연산 빨라짐
ID-GNN summary
1.어떠한 message passing GNNs에 적용가능(GCN, GIN, GraphSAGE)
-
GNN보다 표현력 우수(Cycle count 가능)
-
PyG, DGL등의 GNN 툴을 통해 쉽게 구현 되어있다함
4. Over-smoothing 문제
- GNN Layer를 많이 쌓는다 → receptive field 가 overlap 된다 → 노드 임베딩이 매우 유사해짐 → Over-smoothing 발생
가정 : Raw input graph은 computational graph와 같다
But, 아래의 이유로 가정이 깨짐
1) Feature level
- Input graph의 피쳐 부족 → feature augmentation
2) Structure level
- The graph is too sparse → Message Passing 비효율 → Add virtual node/edge
- The graph is too dense → Message passing의 비용이 커짐 → sampling neighbors
- The graph is too large → 위와 비슷하게 cost 문제 발생 → sampling subgraph
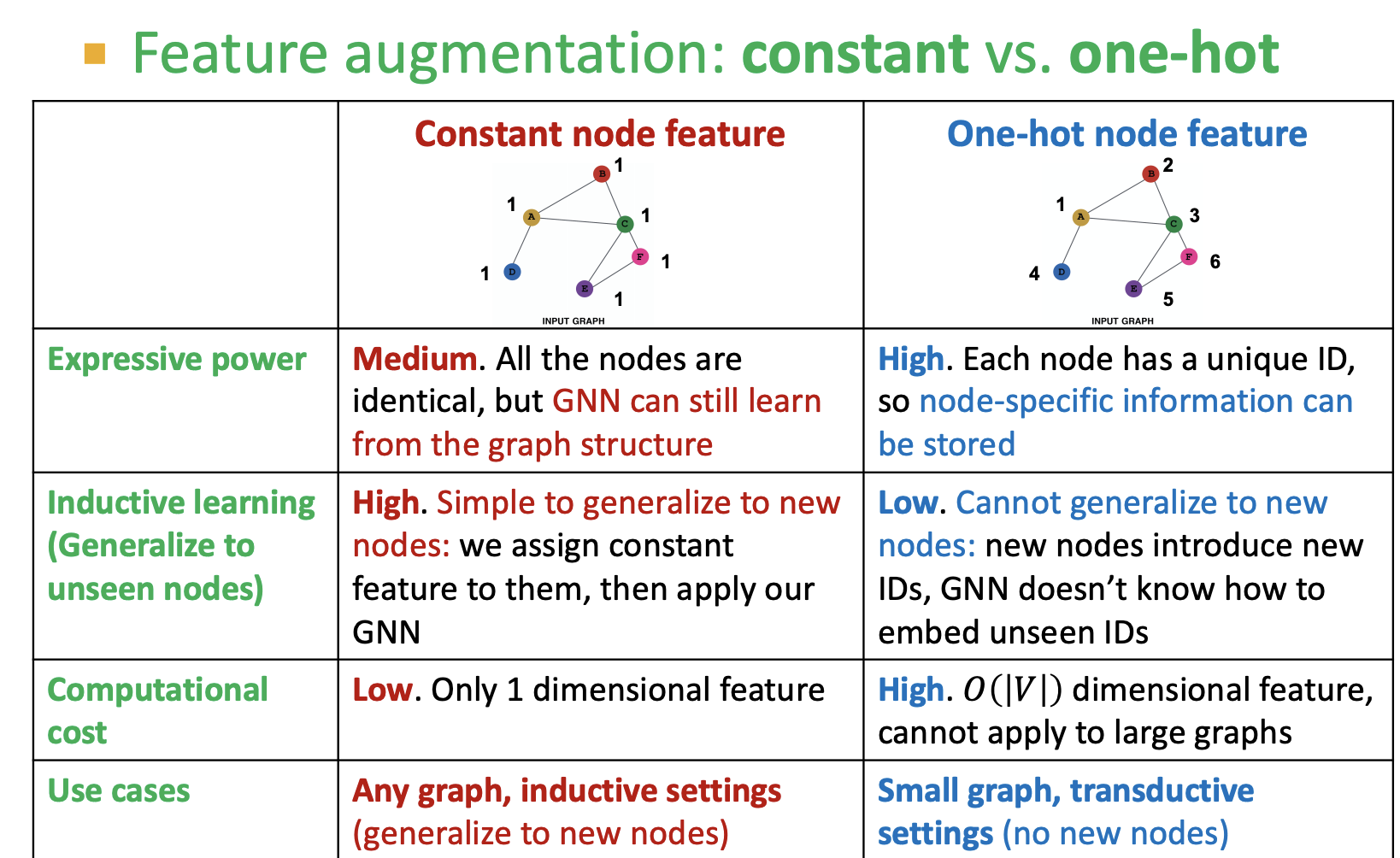
feature augmentation
- 노드에 constant(1) 부여 하거나 One-hot 인코딩 하는 방법이 있음 (constant는 표현력의 한게가, one hot인코딩은 unseen node 대응이 안되는 문제가 있음)
- Cycle 정보를 count하기 위한 값을 부여
- GNN으로 확실하게 학습하기 어려운 구조 정보를 추가(Clustering Coeffcient, Centrality, ...)
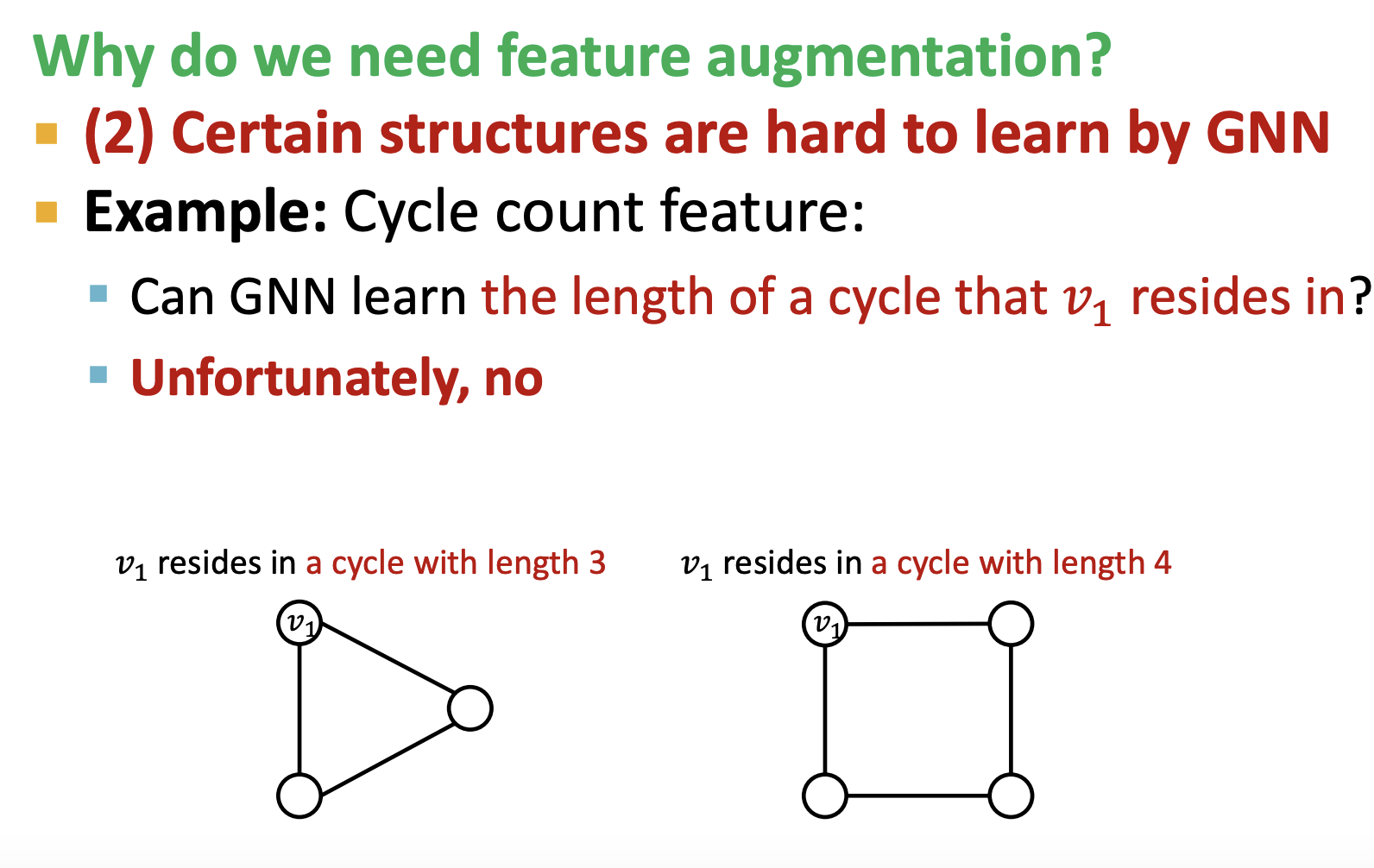
- Virtual edge 추가(sparse data일 경우)
- Adjacency Matrix에 제곱항을 더함
5. Scaling up GNN (Large Graph에 GNN을 적용하는 이슈)
Why is it hard?
- 1) 일반적인 sgd학습 어려움 → tabular data와 달리 neighbor끼리 독립적이지 않음( 그냥 단순한 샘플링 불가)
- 2) full batch 처리도 어려움 → GPU의 한계 ;
두가지 방법이 존재
1) 각 mini-batch 안에서 subgraph 에 대한 message passing neighbors sampling cluster GCN
2) feature-preprocessing operation으로 GNN 단순화 시킴
- simplified GCN
K-layers GNN → k-hop neighborhood aggregation 연산
Neighbor Sampling
- 각 hop 에서 H개 이웃만 Sampling
ex) H가 2일때, 1번 하위 노드 끊음

- H의 크기에 따라 trade-off 존재
- H가 작으면 neighbor agg는 효과적이나 training이 불안정해짐
- GNN layer가 커질수록 Computational cost가 exponential하게 증가하므로 여전히 문제
- random sampling이 쉽고 간편하나 optional 방법이 아님
- 대안은 중요 노드 위주로 sample 을 선정하는 방법
Subgraph Sampling
- Large graph → sampled subgraph → Layer-wise node embedding
Q. GNN training에 subgraph가 어떤식으로 좋게 작용?
- GNN이 edge를 경유하는 message passing을 통해 동작하는 것처럼, Subgraph 또한 가능한 Original graph 구조의 edge 연결성을 보존하도록 설계됨
Q. 어떤 Subgraph 가 GNN학습에 좋을까?
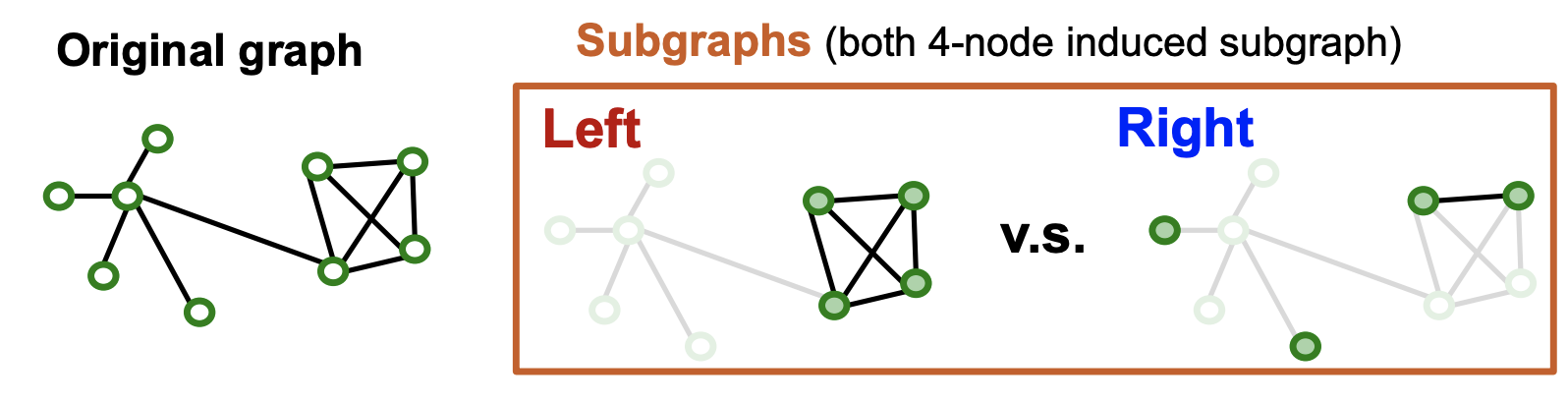
- Left의 경우 커뮤니티 구조 정보가 남아있으므로 좋은 subgraph의 예시 → Good
- Right의 경우 각 node가 동떨어져 있고 연결 패턴이 사라짐 → Bad
Vanilla cluster-GCN
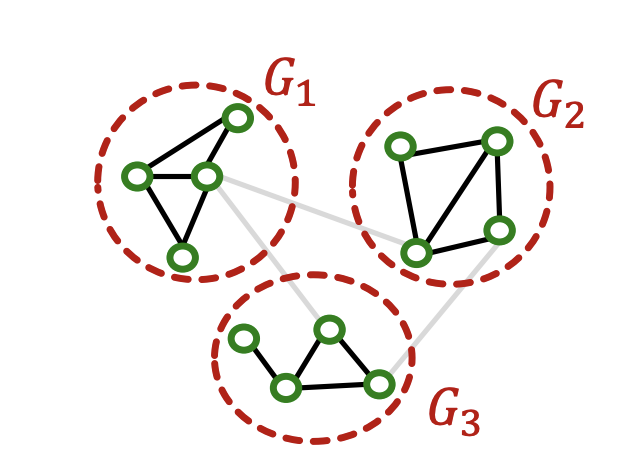
- 커뮤니티 탐지 알고리즘으로 Subgraph 생성(Lovain, etc, ...) 단, 그룹간의 edge는 포함하지 않음
- Layer-wise 노드 임베딩 업데이트
- Vanilla GCN의 한계점
- graph(각 subgraph)간의 연결이 제거됨
- 커뮤니티 탐지 알고리즘은 전체 노드 중 지엽적인 portion으로 묶어질 수 있음
- 샘플된 노드가 전체 그래프 구조를 표현 하는데 충분히 다양하지 않을 수 있음
- 단점을 보완한 알고리즘 Advanced Cluster GCN → 미니 배치당 multiple 노드 그룹을 sampling 하고 aggregation하는 방법(자세한 알고리즘 skip)
- neighbor sample 보다 Clustering GCN이 계산 효율성이 더 좋다함
Simplifying GCN
- GCN에서 Relu 함수 걷어냄
- 연산효율화는 되었으나 non-linearity 의 한계도 존재(상세 파악필요)
- 그럼에도 여러 GNN모델 못지않은 성능이 나오는데 graph homophily 때문일 것(연결된 노드는 같은 label을 갖는 경향)
