[ICLR 2023] TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis

이때까지의 연구와 문제점

기존의 시계열 분석은 1D 시계열(input time-series) 그자체로 모델링 하는것에 집중했다. 하지만, 기존의 방법들과 달리 1D 시계열에서는 시계열의 복잡한 시간패턴을 잘 모델링 할 수 없다.
이 논문에서는 complex temporal variation을 아래의 두가지로 나눈다.

1. multiple intraperiod variantions : 지정된 period내에서의 관계
2. multiple interperiod-variations : 지정된 period들과의 관계
   아래의 그림을보면, 파란색이 interperiod 를 나타내고, 빨간색이 intraperiod를 나타낸다.

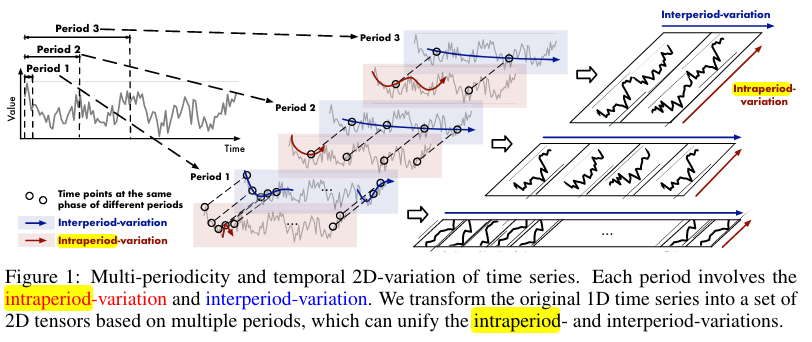
그래서 이 논문에서는!
1D 시계열의 표현 능력에 대한 한계를 해결하기 위해서 1D 시계열을 여러 기간을 기반으로 하는 2D 텐서 세트로 변환한다. 이 논문에서 말하는 변환 이라는 것은 multiple intraperiod variantions 와 multiple interperiod-variations 을 2D의 열과 행으로 삽입해서 2D variation을 2D Kernel로 모델링하기 쉽도록 한다.

삽입하는게 마지막 행과 열에 추가하는건지 전체 열과 행 전체에 영향을 주는건지?

이 논문은 전체 TimesNet이라는 구조안에 TimesBlock이라는 구조가 있다. TimesBlock 구조가 task-general backbone으로 2D tensor (이 논문에서의 변환을 통한)에서 복잡한 시간 변화를 추출한다.

TimeBlock은 학습된 기간을 기반으로 1D 시계열을 2D 텐서 세트로 변환한다. +Parameter-efficient inception block을 통해서 intraperiod/interperiod variation을 포착해낸다.

어떻게?
이 논문에서는 multi-periodicity와 complex interactions에 영향을 받아서 시작한다. 1D 시계열을 2D 시계열로 변환함으로써 intraperiod와 interperiod 모두에 대해서 볼 수 있다.

multi-periodicity : 다중 주기성

complex interactions : 복잡한 상호 작용

즉, 간단하게 정리하면, 이 논문에서는 1D time-series에 대한 multi-periodicity 측면에서의 새로운 분해(혹은 분석) 기법을 2D Tensor로 변환하는 것이다.

기존의 시계열 데이터가 단순한 trend, Seasonality, Residual등으로만 나누어진다기보다는 좀 더 다양한 주기성을 기반으로 하고 더나아가서 변수들 간의 복잡한 상호작용을 고려하여 분석해야 한다는 것이다.

기존의 시계열 $X_{1D} \in \R^{T \times C}$ : Time length : T , 변수가 C개라고할때, interperiod-variation을 표현하기 위해서 periods(기간)을 먼저 찾아야한다. 이렇게 하기위해서 시계열 데이터를 FFT (Fast Fourier Transform) 도메인으로 변환해서 분석한다.

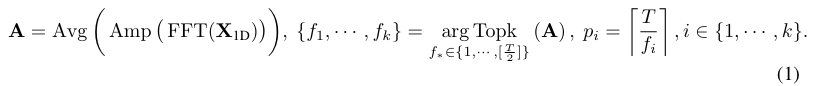
AMP는 calculation of amplitude values으로 A는 각 frequency의 계산된 amplitude(진폭)을 나타내며, 전체 C 차원에 대한 평균 값이다.
AMP는 calculation of amplitude values으로 A는 각 frequency의 계산된 amplitude(진폭)을 나타내며, 전체 C 차원에 대한 평균 값이다. 식 (1)에서는 frequency domain에서의 sparsity때문에 무의미한 high frequency가 생기는 것을 피하기 위해서 Top-K amplitude를 사용한다. (argTopK의 역할)

시계열 데이터를 frequency domain으로 변환하여 분석한 뒤에 2D Tensor로 변환되도록 한다.

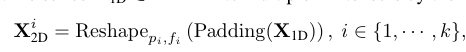
시계열의 1D → 2D 변환이 두 종류의 locality를 가져온다.

1. adjacent time points (columns, intraperiod-variation)
2. adjacent periods (rows, interperiod-variation)

의미있는 2D tensor를 Inception block을 통해서 의미있는 representation을 얻는다.
아래의 구조를 보면, 1D space에서 intraperiod-variation과 interperiod-variation으로 시계열을 나누어서 보는걸 시각적으로 볼 수 있다.

마지막에는 inception block과 reshape을 통해서 1D로 바꿔서 최종 테스크를 위한 aggregation을 통과한다.
최종단계에서 사용하는 adaptive aggregation은 Autoformer의 Auto-Correlation로부터 영감을 받았다고 한다. 각 Amplitude의 softmax값들의 곱으로 최종 $X^l_{1D}$을 계산한다.

소감..
1D time-series를 2D-variation으로 바꾸면, 비전 모델로서의 접근 또한 가능해진다. 이게 이 논문의 큰 장점이 아닐까 하는 생각이 들었다.
5가지 시계열의 분야에 대해서 전부 실험 한 건 시계열 연구를 하는 나에게 큰 자극을 주는 것 같다. 나도 다음에 시계열 연구할때 끝판왕 모델을 만들고 싶다는 생각이 든다.