[Logistic 회귀] ln(Odds)의 분포

이번 포스팅에서는 흔히들 정규분포를 따른다고 하는 $\ln(Odds)$ 가 정확히 어떤 분포를 따르는지 관찰해보겠습니다.

먼저 $\ln(Odds)$ 는 엄밀히 말하면 분포가 아니라 함수입니다.

이것이 어떤 분포를 따르는지 관찰하겠다는 것은
특정 분포를 따르는 $X$ 를 $\ln(Odds)$ 에 넣었을 때 생겨나는 $\ln(Odds(X))$ 가 어떤 분포를 따르는지 관찰하겠다는 말과 같습니다.

여기서 우리의 관심사는 $X$ 가 아닌 $\ln(Odds)$ 이므로 $X$ 는 최대한 무난한 분포로 고르는 것이 좋겠죠.

따라서 $X$ 를 다음과 같은 확률밀도함수를 가지는 분포로 정의하겠습니다. (굉장히 무난무난하죠)

$\qquad f(x) = 1 \qquad (0 \lt x \lt 1)$

그리고 $\ln(Odds(X)) = \ln(\dfrac{X}{1-X}) = T$ 라 하고, $T$ 의 확률밀도함수를 구해보겠습니다.

유도를 위한 핵심 아이디어는 다음과 같습니다.

$\ln(Odds)$ 는 $0.5$를 $0$으로, $x$를 $\ln(\dfrac{x}{1-x})$ 로 대응시킨다.

따라서 $P(0.5 < X < x) = P(0 < T < \ln(\dfrac{x}{1-x}))$ 이다. $\qquad\cdots\space①$

여기서 $\ln(\dfrac{x}{1-x}) = t$ 라 하고 $x$ 에 관해 정리하면,

$\qquad\Rightarrow \dfrac{x}{1-x} = e^t$

$\qquad\Rightarrow x = e^t - xe^t$

$\qquad\Rightarrow (e^t+1)x = e^t$

$\qquad\Rightarrow x = \dfrac{e^t}{1+e^t}$

$\qquad\Rightarrow x = \dfrac{1}{e^{-t}+1}$

이므로 $①$ 을 다음과 같이 바꾸어 쓸 수 있습니다.

$P(0.5 < X < \dfrac{1}{e^{-t}+1}) = P(0<T<t)$

$X$의 확률밀도함수가 $y = f(x) = 1$ 이므로

$\qquad P(0.5 < X < \dfrac{1}{e^{-t}+1}) = \dfrac{1}{e^{-t}+1} - 0.5$

입니다.

그리고 $T$ 의 확률밀도함수를 $y = g(t)$ 라고 하면 $P(0<T<t) = \int_{0}^{t}g(x)dx$ 이므로 다음이 성립합니다.

$\int_{0}^{t}g(x)dx = \dfrac{1}{e^{-t}+1} - 0.5$

양변을 $t$에 대해 미분하면

$\qquad g(t) = \dfrac{d}{dt}(\dfrac{1}{e^{-t}+1})$

$\qquad\Rightarrow g(t) = -\dfrac{-e^{-t}}{(e^{-t}+1)^2} = \dfrac{e^{-t}}{(e^{-t}+1)^2}$

엄밀히 말하면 정규분포의 확률밀도함수는 아니지만 그래프를 그려보면 개형이 정규분포와 유사합니다.

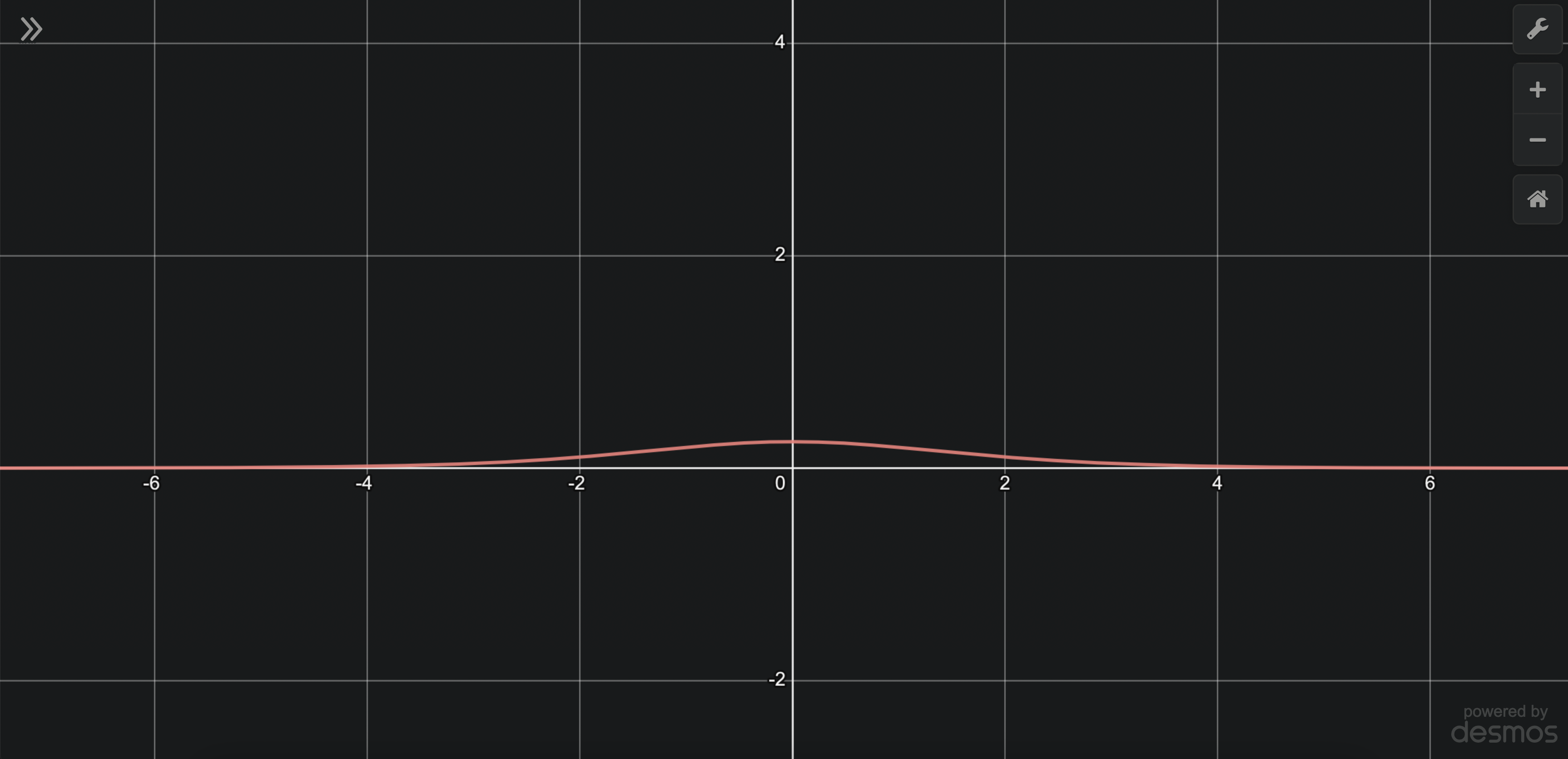
만약 $X$의 확률밀도함수에 조금 변화를 준다면 $\ln(Odds(X))$ 의 확률밀도함수가 정확히 정규분포의 그것과 일치하게 될 수도 있지 않을까 하는 생각이 듭니다.

---

이번 포스팅에서는 $\ln(Odds)$ 가 만들어내는 분포에 대해 살펴보았습니다.

감사합니다.