Machine Learning

이번 포스팅에서는 최소자승법을 이용한 단순선형회귀에서 회귀계수들을 구하는 방법과 실제 계산 과정을 다루어보려고 합니다.즉, 다음과 같은 설명변수 $X$와 종속변수 $Y$에 대해$X = {x_1, x_2, x_3, ... \\space, x_n}$$Y = {y_1, y_

지난 포스팅에서는 최소제곱법을 이용한 단순선형회귀의 회귀계수를 구해보았습니다.이번 포스팅에서는 회귀계수 $\\beta_1$과 $(X, Y)$의 상관계수 사이의 관계를 탐구해보려고 합니다.$\\qquad X = {x_1, x_2, x_3, ... \\space, x_n}

지난 포스팅에서는 회귀계수와 상관계수 사이의 관계를 알아보았습니다.이번 포스팅부터는 회귀모델의 평가지표인 $R^2$ 과 상관계수 $r$ 사이의 관계를 알아보겠습니다.하지만 그 전에 다음 공식을 먼저 이해해야 합니다.$\\qquad SST = SSR + SSE$$i$번째

지난 포스팅에서는 최소제곱법을 이용한 선형회귀에서 $SST = SSR + SSE$ 임을 증명했습니다.이번 포스팅에서는 마찬가지로 최소제곱법을 이용한 선형회귀에서 결정계수 $R^2$이 상관계수 $r$의 제곱과 같음을 보이도록 하겠습니다.결정계수는 회귀모델의 성능을 평가하

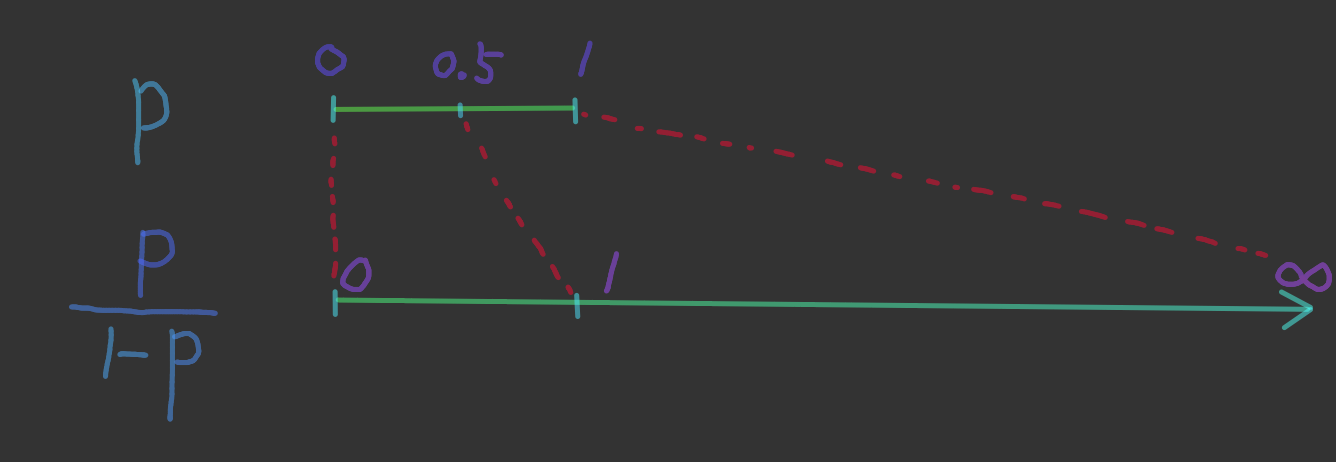
앞으로 몇 포스팅에 걸쳐 Logistic 회귀에 대해 다루어보려고 합니다.Logistic 회귀는 회귀를 이용하여 분류 문제를 해결하는 방법론인데요.이를 이해하려면 먼저 Odds 에 대해 이해해야 합니다.Odds(오즈)는 확률에 관한 용어로, 어떤 사건이 일어날 확률을

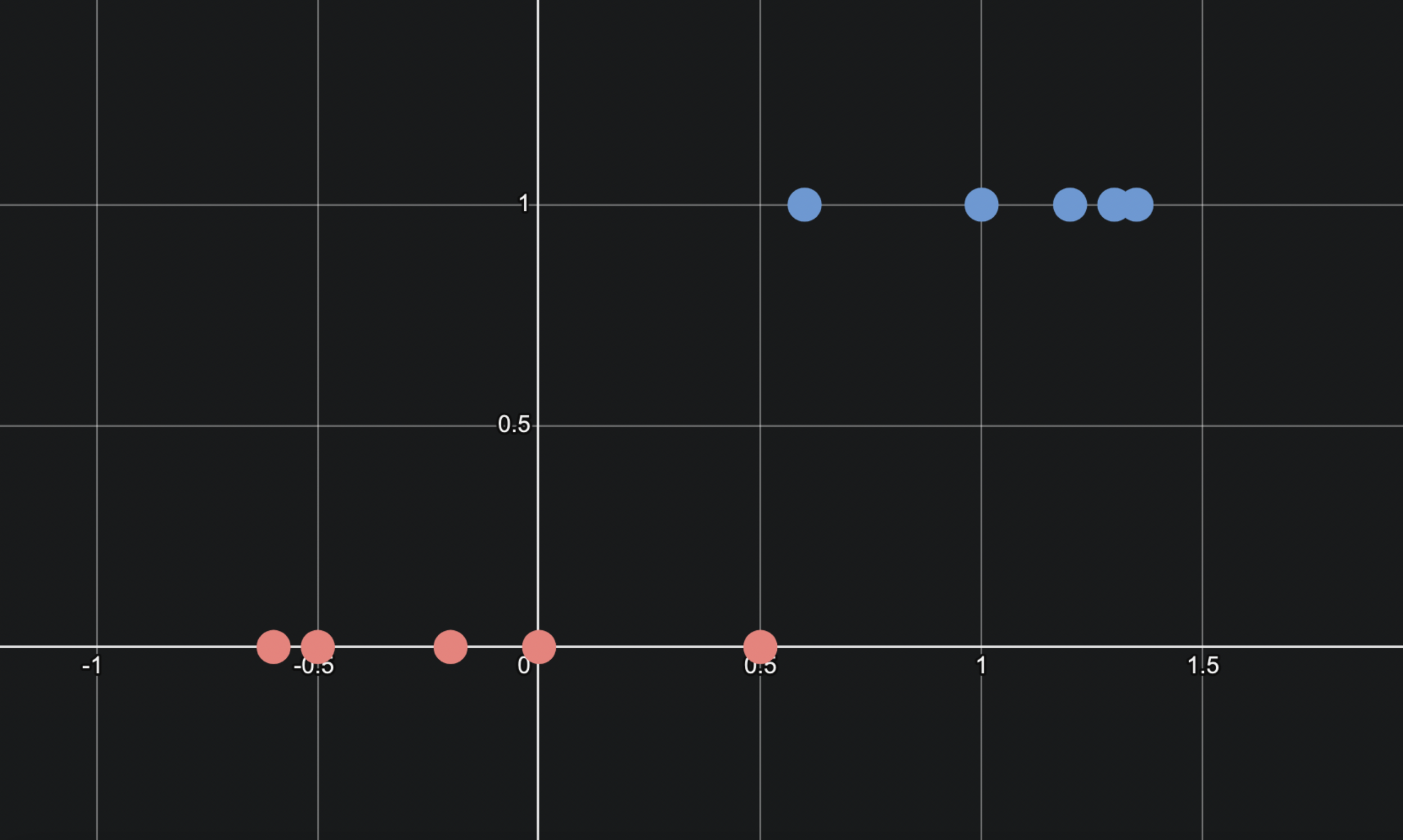
지난 포스팅에서는 Odds 에 대해 알아보았습니다.이번 포스팅에서는 본격적으로 Logistic 회귀에 대해 알아보려고 합니다.아래와 같은 데이터를 살펴보겠습니다.x축은 설명변수, y축은 0과 1만을 가질 수 있는 이진형 종속변수입니다.우리는 이 데이터를 나타낼 수 있는

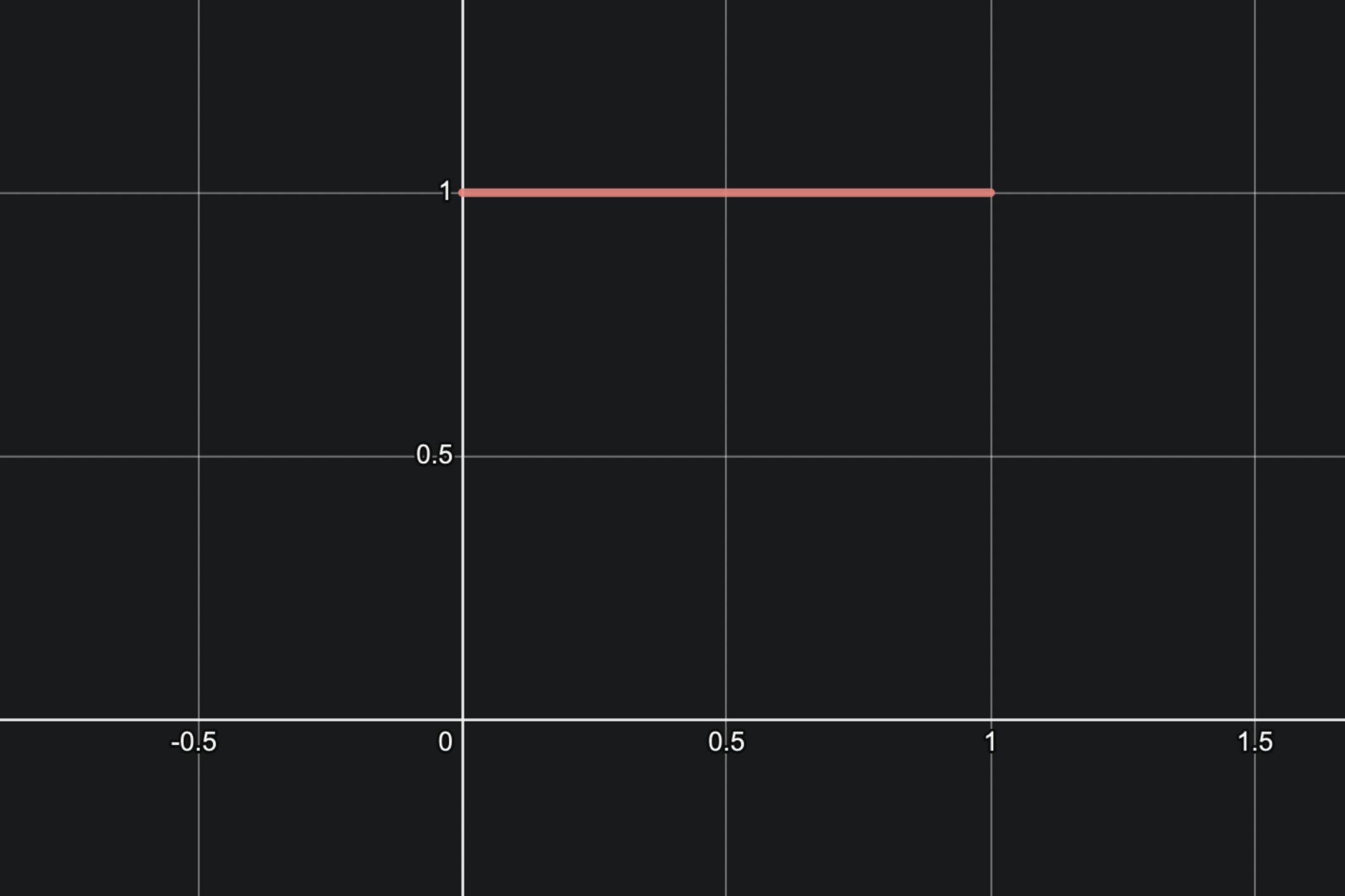
이번 포스팅에서는 흔히들 정규분포를 따른다고 하는 $\\ln(Odds)$ 가 정확히 어떤 분포를 따르는지 관찰해보겠습니다.먼저 $\\ln(Odds)$ 는 엄밀히 말하면 분포가 아니라 함수입니다.이것이 어떤 분포를 따르는지 관찰하겠다는 것은특정 분포를 따르는 $X$ 를

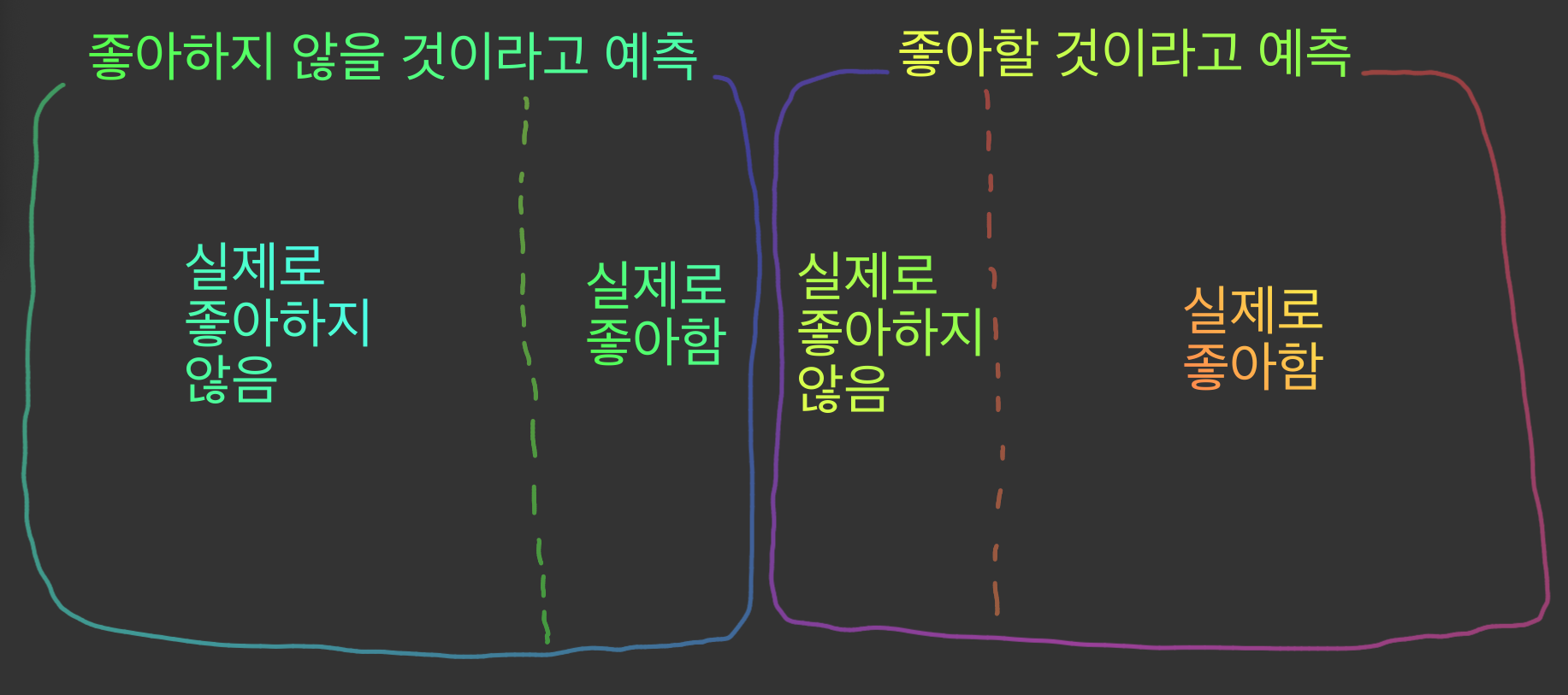
이번 포스팅에서는 분류모델의 평가지표에서 핵심이 되는 TN, TP, FN, FP에 대해 알아보겠습니다.구체적인 맥락과 함께 이해하기 위해 알 수 없는 유튜브 알고리즘(영상 추천 모델)을 생각해보겠습니다.이 모델은 어떤 사용자가 특정 영상을 좋아할지, 좋아하지 않을지를