분류, 회귀, 다중 출력이 모두 가능하다고??

1) training

iris dataset에서 두 피처(petal length, petal width)를 이용하여 분류 모델을 학습하고 시각화한 결과이다. 데이터는 depth=0인 root node에서 시작하여 자식 노드가 없는 leaf node까지 이동한다. 만약 petal length가 2.45보다 작거나 같다면 depth=1인 왼쪽 노드로 이동하게 되고, 이는 하나의 피처로만 구성된 순수 노드이기 때문에 class=setosa에서 알 수 있듯, setosa로 분류됨을 알 수 있다. 그리고 만약에 petal length가 2.45보다 크고 width가 1.75보다 작거나 같다면 depth=2의 왼쪽 노드까지 이동하게 되며 class=versicolor에 따라 이로 분류됨을 알 수 있다.

노드마다 gini, samples, value, class 파라미터가 있는 것을 볼 수 있다. 파라미터들이 의미하는 바는 다음과 같다.

• samples: 노드에 속한 training instance의 수
• value: 노드에 속한 training instance들이 각 class 당 얼마나 있는지
• gini: impurity(불순도)
  • Gini impurity
    $G_i=1-\sum_{k=1}^n{{p_{i,k}}^2}$
    • $G_i$: i번째 노드의 gini score
    • $p_{i,k}$: i번째 노드에서 총 training instance 중 class k의 비율
  • 정의: Gini impurity measures how often a randomly chosen element of a set would be incorrectly labeled if it were labeled randomly and independently according to the distribution of labels in the set.
    -> 랜덤하게 뽑힌 instance들이 얼마나 잘못 라벨링(=예측)되었는지 측정함
  • 노드에 속한 training instance들이 모두 하나의 클래스에 속하는 경우를 "pure"이라고 하며 이때 gini=0이다.
  • 예를 들어, depth=2의 왼쪽 노드의 gini score는 $1-(0/54)^2-(49/54)^2-(5/54)^2\approx0.168$이다.
• class: 예측 클래스

from sklearn.tree import DecisionTreeClassifier

tree_clf = DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X, y)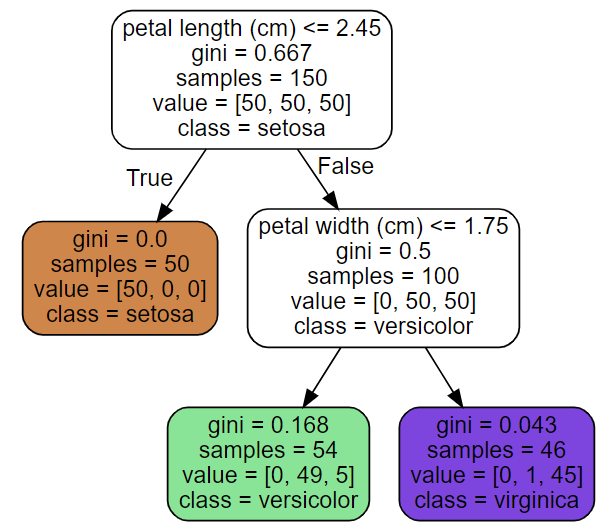

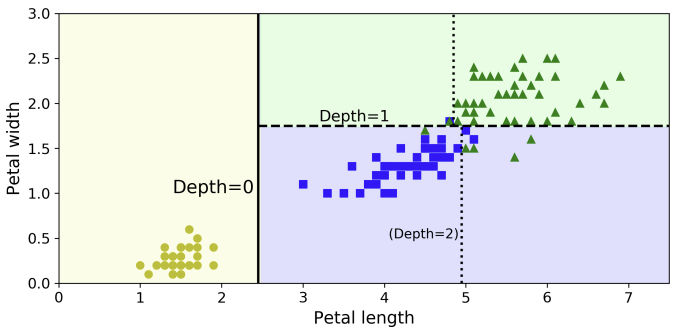
아래 그림은 decision tree의 decision boundary를 나타낸 것이다. 수직인 직선은 root node(Depth=0)의 결정 경계선(petal length=2.45)을 나타낸다. 이 선을 기준으로 Iris-Setosa만 있는 왼쪽은 pure하고, 오른쪽은 impure하기 때문에 Depth=1에서 petal width=1.75를 기준으로 굵은 점선으로 나뉜다. 위 모델을 만들 때 max_depth=2로 설정하였기에 분기는 여기서 멈춘다.

2) Probabilities

decision tree는 어떤 instance가 특정 class k에 속할 확률을 추정할 수 있다.

먼저 root node에서 시작하여 순서대로 이 instance가 속한 leaf node를 찾는다. 예를 들어 petal length=5, petal width=1.5인 instance가 있다고 하면, 이는 depth=2의 왼쪽 노드에 도달하게 될 것이다. 그 다음에는 Iris-Setosa에 대해 0 (0/54), Iris-Versicolor에 대해 0.907 (49/54), Iris-Virginica에 대해 0.093 (5/54)을 반환하게 된다.

tree_clf.predict_proba([[5, 1.5]])
# array(([0. , 0.907, 0.093]])

결과적으로 예측하는 클래스는 가장 높은 확률을 가지는 클래스가 된다.

tree_clf.predict([[5, 1.5]])
# array([1])

3) CART algorithm

CART algorithm은 Classification And Regression Tree로, 이름에서 알 수 있듯이 분류와 회귀 문제에서 사용된다. 먼저, 이 알고리즘은 단일의 피처 k 와 threshold $t_k$ 를 이용하여 training set을 두 개의 subset으로 분리한다. 이때 k와 $t_k$는 CART 손실함수를 최소화하는, gini 불순도를 최소화하는, 즉 가장 순수한 subset을 만드는 방향으로 구해야 한다.

CART cost function for classification

• $G_{\text{left/right}}$: left/right subset의 (gini) impurity
• $m_{\text{left/right}}$: left/right subset의 instance 수

분기는 이 알고리즘을 이용하여 계속되며, max_depth가 설정된 경우에는 해당 depth에서 멈추고, 설정되지 않은 경우에는 impurity가 감소하는 split을 찾지 못할 때 멈춘다.

*greedy algorithm: CART 알고리즘은 최상의 레벨에서 최적의 split을 찾기 때문에 아래 레벨의 split에서 가장 낮은 impurity level을 갖는지에 대해 고려하지 않는다. 그래서 때로는 합리적이지만 최적의 tree를 보장하지는 않는다.

*NP-Complete Problem: 최적의 tree를 찾는 법

• 시간 복잡도: $O(exp(m))$
• 매우 작은 훈련셋에 적용하기 어려움

4) Computational Complexity

예측 과정에서 데이터는 나무의 root node에서 leaf node까지 이동하고, 의사결정 나무는 일반적으로 균형잡힌 형태를 띄고 있고, 예측 과정에서는 피처의 수가 관련이 없기 때문에, decision tree를 순회하면 대략 $\log_2 (m)$개의 노드를 지나치게 되므로 시간 복잡도는 $O(\log_2 (m))$이다.

*왜 $O(\log_2 (m))$개의 노드냐?
-> 총 샘플 수가 m개, 나무의 높이가 h일 때, $m\approx2^h$이므로 $h\approx \log_2 (m)$기 때문
-> binary

그러나, 학습 과정에서 알고리즘은 max_depth가 설정된 경우를 제외하고는, 각 노드에서 모든 샘플들을 모든 피처에 대해 비교하기 때문에 시간 복잡도는 $O(n\times m\log_2 (m))$가 된다.

*m: 샘플 수, n: 피처 수

5) Gini Impurity or Entropy?

엔트로피란 불순도를 측정하는 지표로서 정보량의 기댓값이다. 정보 이론에서 엔트로피는 다음과 같이 나타낼 수 있다.

• S: 발생한 사건의 집합
• c: 사건의 수

이때 정보량이란 어떤 사건이 가지고 있는 정보의 양을 의미하며, 이를 식으로 나타내면 다음과 같다.

• p(x): 사건 x가 발생할 확률

이 식에 따르면 사건 x가 발생할 확률이 증가할수록 정보량은 0에 수렴하게 된다. 즉, 자주 발생하는 사건일수록 정보량이 많지 않다는 것을 알 수 있다.

이를 바탕으로 결정트리의 특정 노드에서 엔트로피는 다음과 같이 나타낼 수 있다. (식 앞에 붙은 -는 정보량에 해당하는 로그 식을 정리할 때 나온 것이다.)

*When to use?
-> 둘 사이에 차이는 거의 없지만, gini 불순도의 계산 속도가 조금 더 빠르며, gini 불순도는 가장 많이 나타나는 클래스를 자기 branch에서 나누려고 하지만, entropy는 비교적 균형 있는 나무를 만들려고 한다.

6) Regulation Hyperparameters

nonparametric

• 예: decision trees
• 학습 전에 파라미터의 수가 결정되지 않음
• overfitting의 위험이 있음

parametric

• 예: linear models
• 파라미터의 수가 미리 결정됨
• degree of freedom이 제한됨
• overfitting 위험이 적음

decision tree의 이러한 특성 때문에 학습 도중에 freedom을 제한해야 한다. 이는 regularization이라고 하며, 여러 하이퍼파라미터를 이용하여 수행할 수 있다.

• max_depth: 최대 깊이 설정
• min_samples_split: split 하기 전에 노드가 가지고 있어야 할 최소 샘플 수
• min_samples_leaf: leaf node가 가지고 있어야 할 최소 샘플 수
• min_weight_fraction_leaf: min_samples_leaf와 같지만, 가중치가 부여된 샘플 수에서의 비율
• max_leaf_nodes: leaf node의 최대 수
• max_features: 각 노드를 나누는 데 평가하는 데 사용되는 피처의 최대 수

그러므로 min 어쩌구를 증가하는 거나 max 어쩌구를 감소하는 건 모델을 규제하는 방법이 된다.

7) Regression

X에 랜덤한 하나의 입력 특성을, y에 노이즈가 포함된 X에 대한 이차 함수를 넣었다. 이 데이터를 이용해서 결정트리를 그리면 다음과 같다.

분류와 회귀에서의 차이는 각 노드에서 클래스를 예측하는 대신 어떤 value를 예측한다는 것이다. 여기서 예측값 value는 각 노드에 있는 샘플들의 평균 타깃값이다.

회귀 모델의 max_depth 파라미터를 3으로도 설정하여 분할을 나타내보았다. (파란점들은 샘플들을, 빨간선들은 각 구간에서 평균 예측값(타깃값)을 의미한다.)

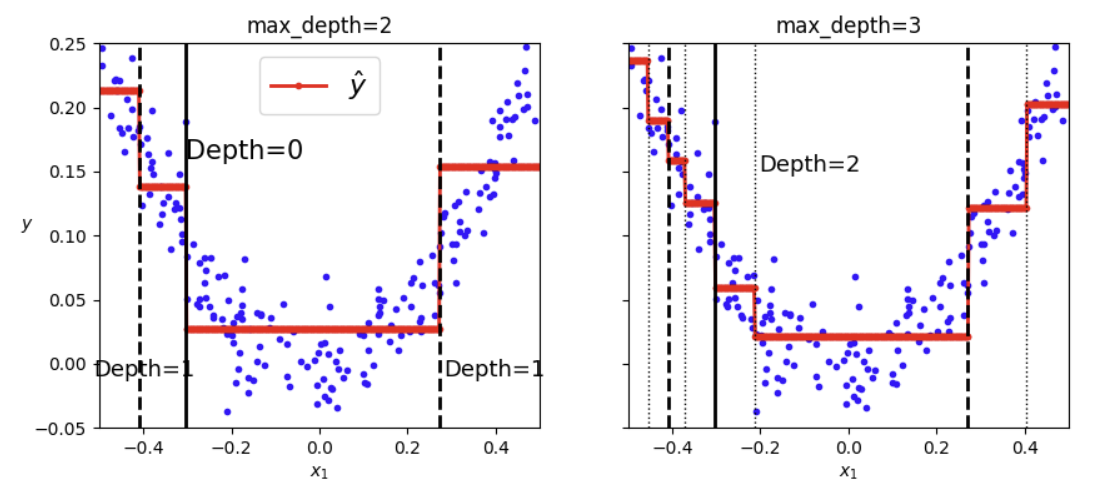
CART 알고리즘은 앞에서 훈련셋의 impurity를 최소화하는 방향으로 분할했던 것과 달리, 회귀에서는 훈련셋의 MSE를 최소화하도록 훈련셋을 나눈다.

CART cost function for regression

• $\text{MSE}_{\text{node}}=\sum_{i\in \text{node}}(\hat{y}_{\text{node}}-y^{(i)})^2$
• $\hat{y}_{\text{node}}=\frac{1}{m_{\text{node}}}\sum_{i\in \text{node}}y^{(i)}$

여기서도 규제를 통해 overfitting을 방지할 수 있다.

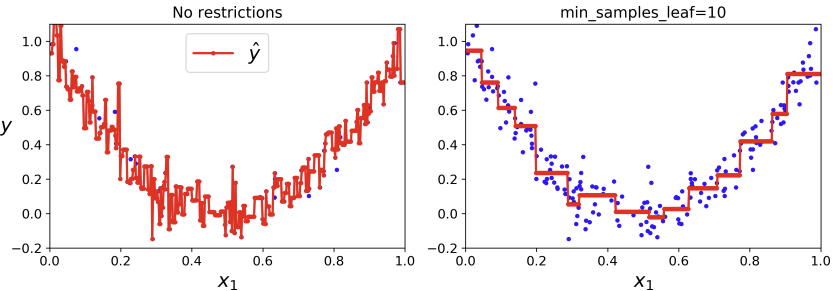
from sklearn.tree import DecisionTreeRegressor

tree_rg = DecisionTreeRegressor(max_depth=2)
tree_rg.fit(X, y)

8) Instability

8-1) orthogonal decision boundaries

training 단계에서 결정 경계선 그림에서 확인할 수 있듯, decision tree의 결정 경계선은 축과 직교한다. 그래서 왼쪽과 같이 데이터가 선형적으로 분리할 수 있는 경우에는 잘 작용하지만, 오른쪽과 같이 데이터가 45도 회전한 경우에는 결정 경계선이 불필요하게 데이터를 돌돌(?) 감싸는 것을 볼 수 있다.

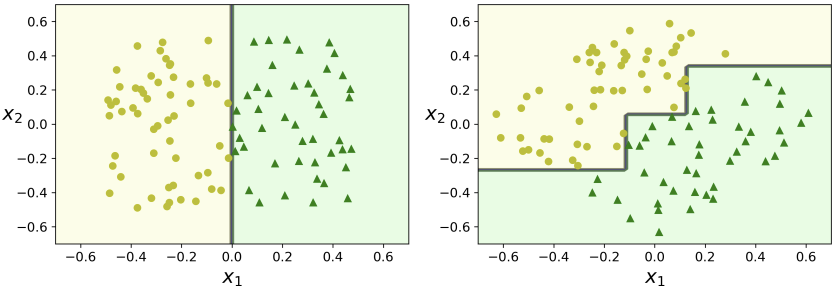
8-2) sensitive to small variations

이전의 데이터셋에서 petal length=4.8, petal width=1.8인 하나의 데이터만 없애더라도 결정 경계선이 다르게 형성되는 것으로 보아, 작은 변화에도 민감하게 반응하는 것을 알 수 있다. 또한, 사이킷런에서 사용하는 training algorithm이 stochastic하기 때문에 random_state 파라미터를 설정하지 않는 이상, 같은 데이터셋에 대해서도 결정 경계선이 다르게 형성되어 모양이 다른 의사결정 나무를 만들게 된다.

이러한 문제들을 해결하기 위해 많은 나무들의 prediction을 평균하여 instability를 줄이는 Random Forest가 나온다.

출처: Hands-On Machine Learning by Aurelien Geron
https://leedakyeong.tistory.com/entry/Decision-Tree%EB%9E%80-ID3-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98