★ 해시
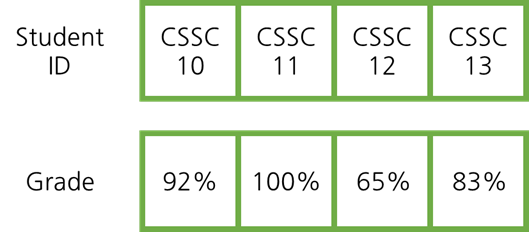
연결 리스트의 단점은 리스트에서 무언가를 찾고 싶을 때 무조건 모든 요소를 살펴봐야 한다는 것입니다. 이러한 단점을 해결하여, 데이터를 빠르게 추가하거나 제거하도록 한 데이터 구조가 해시입니다.
해시는 키, 그리고 그와 연관된 값을 가지고 있습니다. 모든 요소를 살펴본 후 동일한 노드를 찾는 연결 리스트와 달리, 해시에서는 키가 주어지면 바로 그와 연관된 값을 찾을 수 있습니다.
해시 함수

해시 함수(hash function)는 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑하는 함수입니다. 해시 테이블이라는 자료구조에 사용되며, 매우 빠른 데이터 검색을 위한 컴퓨터 소프트웨어에 널리 사용됩니다.
해시 충돌
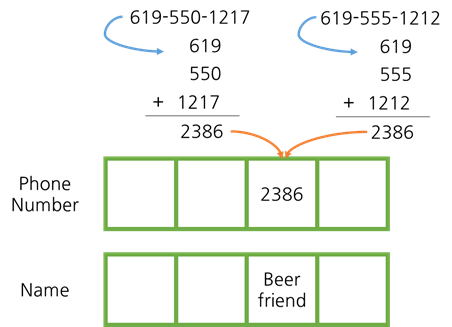
서로 다른 값들의 해시 함수 결과인 키가 일치하는 경우를 해시 충돌이라고 합니다. 예를 들어, 위 사진에서는 전화번호를 3분할한 것의 합을 해시 함수로 지정하였습니다. 그런데 키가 2386으로 같아 해시 충돌이 발생합니다.
해시 충돌을 해결하는 방법
-
선형 조사법(linear probing)
채우려는 공간이 이미 차 있다면, 비어있는 칸을 찾을 때까지 다음 칸을 확인하는 방법입니다. 비어있는 칸을 찾아 그 곳에 채운 후 위치가 바뀌었다는 사실을 알려야 합니다.
-
2차식 조사법(quadratic probing)
다음 칸 대신 1부터 순서대로 제곱하여 더한 칸을 확인하는 방법입니다. 테이블의 끝을 넘어간다면 % 연산을 해서 다시 테이블의 범위 안에 들어오게 합니다.
-
이중 해싱(double hashing)
hashCode 함수가 2개 있어 채우려는 공간이 이미 차 있다면 두 hashCode의 결과를 더한 값을 테이블 내의 위치가 되게 하는 방법입니다.
이중 해싱은 아예 다른 해시 함수를 사용할 수 있기 때문에 데이터를 더 골고루 넣을 수 있습니다. 하지만 해시 함수가 2개 필요하다는 단점이 있습니다. -
체이닝(Chaining)
체이닝(Chaining)은 요소마다 연결 리스트를 만들어 수많은 데이터를 수용할 수 있게 하는 방법입니다. 체인 해시는 가장 안정적이고 보편적으로 사용되는 자료 구조 중 하나입니다.
체이닝을 하면 수용 가능한 요소 개수에 제한이 없어지고 크기 조정도 자주 할 필요가 없어집니다. 적재율 λ는 항목의 개수를 가능한 체인 개수로 나눈 값입니다. 체인 1개에 여러 항목을 넣을 수 있어 λ는 1보다 큰 수가 될 수 있습니다.
하지만 hashCode가 같은 숫자만 반환하여 하나의 체인이 너무 길어지면 결국 연결 리스트와 시간 복잡도가 같아지는 문제가 발생합니다.
재해싱
체인 해시에서 해시가 너무 많이 차면 크기 조정을 해야 합니다.
-
크기가 2배인 배열을 만듭니다.
-
아래 코드에 따라 data의 index를 다시 결정하여 연결 리스트의 요소들을 옮깁니다.
연결 리스트의 위치를 그대로 하여 옮기면 정보를 다시 찾거나 제거하려 할 때 문제가 발생합니다. 정보의 위치를 지정할 때 다른 정보는 그대로인데, tableSize만 바뀌기 때문입니다. 그래서 각 요소의 위치를 초기화한 후, 처음부터 다시 위치를 지정해주어야 합니다.
// data의 index 결정에 hashCode 이용
int idx = x.hashCode(s);
// hashCode가 음수가 되는 경우도 있어서 전부 양수로 바꿔줌
idx = idx & ox7FFFFFFF;
// 테이블의 크기보다 큰 값이 나오면 테이블 범위 안의 인덱스로 바꿔줌
idx = idx % tableSize; 구현
public class Hash<K, V> {
class HashElement<K, V> implements Comparable<HashElement<K, V>> {
// 키와 값 정의
K key;
V value;
// 생성자
public HashElement(K key, V value) {
this.key = key;
this.value = value;
}
// compareTo 메서드 오버라이드
@Override
public int compareTo(HashElement<K, V> o) {
return (((Comparable<K>) this.key).compareTo(o.key));
}
}
// 변수
int numElements, tableSize;
double maxLoadFactor;
LinkedList<HashElement<K, V>>[] hash_array;
// 해시 구현
public Hash(int tableSize) {
this.tableSize = tableSize;
hash_array = (LinkedList<HashElement<K, V>>[]) new LinkedList[tableSize]; // 형 변환
// 연결 리스트 체이닝
for (int i = 0; i < tableSize; i++)
hash_array[i] = new LinkedList<HashElement<K, V>>();
maxLoadFactor = 0.75;
numElements = 0;
}
// 현재 적재율 구하기
public double loadFactor() {
return (double) numElements / tableSize;
}
// 원소 추가
public boolean add(K key, V value) {
// 기준 최대 적재율보다 현재 적재율이 크면 resize
if (loadFactor() > maxLoadFactor)
resize(tableSize * 2);
// 키와 값을 저장해 놓을 object he 정의
HashElement<K, V> he = new HashElement(key, value);
// he의 index 찾기
int hashval = key.hashCode();
hashval = hashval & 0x7FFFFFFF;
hashval = hashval % tableSize;
// add he
hash_array[hashval].add(he);
numElements++;
return true;
}
// 원소 제거
public boolean remove(K key, V value) {
HashElement<K, V> he = new HashElement(key, value);
// index 찾기
int hashval = key.hashCode();
hashval = hashval & 0x7FFFFFFF;
hashval = hashval % tableSize;
// 해당하는 index의 키와 값 제거
hash_array[hashval].remove(he);
numElements--;
return true;
}
// 원소 조회
public V getValue(K key) {
// 해당하는 index 찾기
int hashval = key.hashCode();
hashval = hashval & 0x7FFFFFFF;
hashval = hashval % tableSize;
// 그 index를 찾을 때까지 반복
for (HashElement<K, V> he : hash_array[hashval]) {
if (((Comparable<K>) key).compareTo(he.key) == 0) {
return he.value;
}
}
return null;
}
// 사이즈 증가
public void resize(int newSize) {
// 새로운 체인 해시 생성
LinkedList<HashElement<K, V>>[] new_array = (LinkedList<HashElement<K, V>>[]) new LinkedList[newSize];
for (int i = 0; i < newSize; i++)
new_array[i] = new <LinkedList<HashElement<K, V>>[];
// index에 맞게 값 채워넣기
for (LinkedList<HashElement<K, V>> linkList : hash_array) {
for (HashElement<K, V> hElement : linkList) {
V val = getValue(hElement.key);
HashElement<K, V> he = new HashElement<K, V>(hElement.key, val);
int hashVal = (hElement.key.hashCode() & 0x7FFFFFFF) % newSize;
new_array[hashVal].add(he);
}
}
// 새 배열로 교환해주고, 사이즈도 갱신
hash_array = new_array;
tableSize = newSize;
}
// 키에 연결된 연결 리스트의 내용을 살펴보기
class IteratorHelper<T> implements Iterator<T> {
T[] keys;
int position;
// key반복자 사용
public IteratorHelper() {
keys = (T[]) new Object[numElements];
int p = 0;
for (int i = 0; i < tableSize; i++) {
LinkedList<HashElement<K, V>> list = hash_array[i];
for (HashElement<K, V> h : list)
keys[p++] = (T) h.key;
}
position = 0;
}
// 끝을 확인할 때 사용
@Override
public boolean hasNext() {
return position < keys.length;
}
// 해시의 전체 내용을 살펴보는 함수
@Override
public T next() {
if (!hasNext())
return null;
return keys[position++];
}
}
}
