[백준 - 16399번] 드라이브 - Java

문제 링크

https://www.acmicpc.net/problem/16399

문제

티어: 골드 1
알고리즘: dp

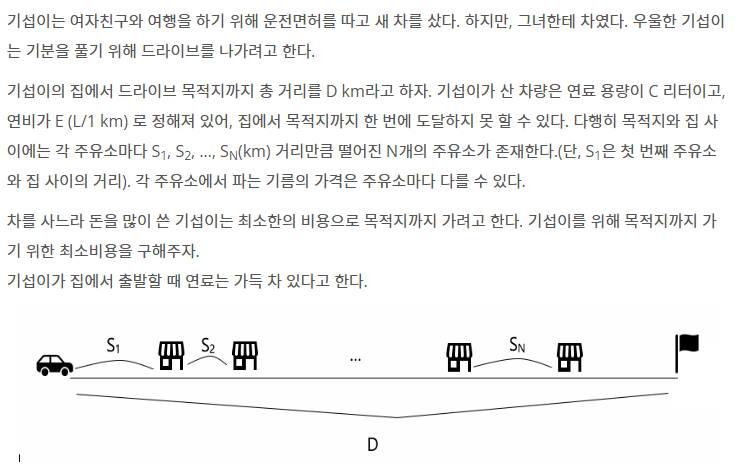
입력

첫 번째 줄에 차량의 최대 연료 용량 C, 차량이 1km가는 동안 사용하는 기름의 양 E, 목적지까지의 거리 D가 주어진다.

두 번째 줄에는 주유소의 개수 N이 주어진다. N=0이면 더 이상의 입력이 주어지지 않는다.

세 번째 줄에는 각 주유소 간의 거리(S1, S2, …, SN)가 공백 하나를 사이에 두고 주어진다.

네 번째 줄에는 첫 번째 주유소부터 N번째 주유소까지 기름의 리터당 가격(P1, P2, …, PN)이 공백 하나를 사이에 두고 순서대로 주어진다.

출력

목적지까지 가는데 필요한 기름값의 최소비용을 출력한다.

만약 도착할 수 없을 경우 -1을 출력한다.

제한

• 1 ≤ D ≤ 10,000 1 ≤ S1, S2, …, SN ≤ 10,000
• 1 ≤ C, E ≤ 500, 0 ≤ N ≤ 1,000, 1 ≤ P1, P2, …, PN ≤ 10,000

풀이

목적지까지 가는데 필요한 기름값의 최소비용을 출력해야 한다.

기섭이가 주유소에 도착했을 때
주유를 얼마나 하냐에 따라서 여러 경우로 나눠진다.

만약 첫 주유소에 도착했을 때 남은 연료가 5리터이고, 최대 용량이 8리터이면

• 주유 하지 않음
• 1L 주유
• 2L 주유
• 3L 주유

라는 선택지가 생긴다.

여기서 최선의 선택이라는 것이 없기 때문에 모든 경우를 구해줘야 하는데, 만약 주유를 한 뒤 다음 주유소까지 갔을 때 남은 연료가 같다면, 그 중 가장 적은 비용을 쓴 경우가 최선이 된다.

그래서 각 주유소에서 기섭이의 상태는 C개 존재한다.

이를 토대로 dp를 정의하면 dp[N][C]이며,
dp[2][3]은 2 번째 주유소에 도착했을 때 기섭이의 남은 연료가 3이라는 뜻이다.

그래서 차례대로 주유소에 방문해서 dp를 채우고, 목적지까지 갔을 때 가장 적은 비용을 출력하면 된다.

소스 코드

import java.io.*;
import java.util.*;

class GasStation {
    int x, p;
    GasStation(int x, int p) {
        this.x = x;
        this.p = p;
    }
}

public class Main {
    static int C, E, D, N;
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        C = Integer.parseInt(st.nextToken());
        E = Integer.parseInt(st.nextToken());
        D = Integer.parseInt(st.nextToken());
        N = Integer.parseInt(br.readLine());

        GasStation[] gs = new GasStation[N + 2]; //N+1은 목적지
        gs[0] = new GasStation(0, 0);
        gs[N + 1] = new GasStation(D, 0);
        if (N != 0) {
            StringTokenizer st2 = new StringTokenizer(br.readLine());
            StringTokenizer st3 = new StringTokenizer(br.readLine());
            for (int i = 1; i <= N; i++) {
                int x = gs[i - 1].x + Integer.parseInt(st2.nextToken());
                int p = Integer.parseInt(st3.nextToken());
                gs[i] = new GasStation(x, p);
            }
        }

        long[][] dp = new long[N + 2][C + 1]; //마지막은 목적지
        initDp(dp);

        int fgs = C - (gs[1].x * E);
        if (fgs < 0) {
            System.out.println(-1);
            return;
        }

        dp[1][fgs] = 0;
        for (int i = 1; i <= N; i++) {
            for (int j = 0; j <= C; j++) {
                if (dp[i][j] != Long.MAX_VALUE) {
                    //존재한다면
                    //0 ~ (C - j)까지 주유를 넣는 경우의 수를 넣어준다.
                    int nd = gs[i + 1].x - gs[i].x; //다음 목적지까지 거리
                    for (int k = 0; k <= (C - j); k++) {
                        int curFuel = j + k; //현재 연료.
                        curFuel -= (nd * E);
                        if (curFuel >= 0) {
                            //다음 목적지에 도착했을 때 연료가 0 이상이라면 가능함.
                            dp[i + 1][curFuel] = Math.min(dp[i + 1][curFuel], dp[i][j] + (gs[i].p * k));
                        }
                    }
                }
            }
        }

        long answer = Long.MAX_VALUE;
        for (int i = 0; i <= C; i++) {
            answer = Math.min(answer, dp[N + 1][i]);
        }

        if (answer == Long.MAX_VALUE) {
            answer = -1;
        }
        System.out.println(answer);
    }

    static void initDp(long[][] dp) {
        for (int i = 1; i <= N + 1; i++) {
            for (int j = 0; j <= C; j++) {
                dp[i][j] = Long.MAX_VALUE;
            }
        }
    }
}