문제 링크
문제
서기 2116년, 인간은 더 이상 AI의 상대가 되지 못하게 되었다. 근력, 순발력, 창의력, 사고력, 문제해결능력, 심지어 인간미조차 AI가 인간을 앞선다. AI가 온 지구를 관리하며 이미 인류는 지구의 주인 자리에서 쫓겨난지 오래이다. 그나마 다행인 것은 AI가 인간을 적대적으로 대하지 않고, 도리어 AI가 쌓아올린 눈부신 기술의 발전으로 모든 사람이 무제한적인 재화를 사용할 수 있게 되어 한 세기 전의 사람들이 바라던 돈 많은 백수와 같은 삶을 누릴 수 있게 됐다는 사실이다. 대다수의 인간들은 현재의 상황에 만족하고 더 이상 발전을 포기한 채 놀고 먹으면서 시간을 보내고 있지만 일부 인간들은 인류의 영광을 되찾기 위해 저항군을 조직해 AI에게 투쟁하고 있다.
저항군은 AI에게 승산이 있는 종목을 찾고 있다. 이러한 종목을 가지고 AI에게 승부를 걸어 전 인류에게 도전정신과 인간의 위대함을 증명하고 싶기 때문이다. 저항군의 지도부는 무려 12시간에 걸쳐 AI에게 승산이 있는 종목을 찾기 위한 회의를 진행했다. 회의에서 알고리즘 문제 풀이 대결, 가위불바위총번개악마용물공기보스펀지늑대나무사람뱀 게임, 캐치마인드, 알까기, 스타크래프트, 똥 피하기 게임, 딸기 2비트, 딸기수박당근참외메론 게임, 백일장, 사생 대회 등 다양한 아이디어가 나왔지만 단 0.01%라도 승산이 있어 보이는 종목은 하나도 없었다.
그렇게 모두가 낙담하던 중 누군가가 역사책을 뒤져 인간이 AI에게 승산이 있는 종목을 찾아냈다. 바로 정확히 100년 전에 있었던 이세돌과 알파고의 바둑 대결이었다. 물론 알파고는 그 이후로 발전을 거듭했기에 바둑에서의 승산은 없지만 바둑의 룰을 변형한 Baduk2라는 종목에서는 이세돌이 알파고에게 한 세트를 이긴 것과 같이 인간이 AI에게 승산이 있다고 판단했다.
Baduk2의 룰은 바둑과 거의 유사하지만 양 선수가 돌을 1개씩 번갈아 두는 것이 아니라 2개씩 둔다는 점이 다르다. 서술의 편의를 위해 상하좌우로 인접한 같은 색 돌의 집합을 그룹이라고 하자. 아래의 판에서는 흑의 그룹과 백의 그룹이 각각 3개씩 존재한다.

Baduk2에서는 일반적인 바둑과 동일하게 자신의 돌로 상대방의 그룹을 빈틈없이 에워싸면 갇힌 돌을 죽일 수 있다. 어느 그룹이 빈틈없이 에워싸였다는 것은 그 그룹 내에 빈 칸과 인접해있는 돌이 하나도 없다는 것과 동치이다.
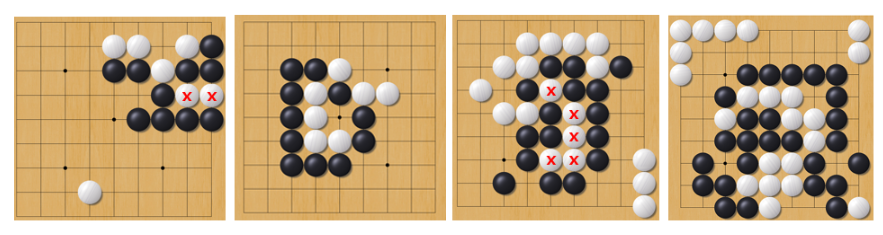
그리고 Baduk2에서는 모든 비어있는 칸에 돌을 둘 수 있다. 설령 상대 돌로 둘러싸여 있어 스스로 잡히는 곳이라고 하더라도 상관이 없다. 아래와 같은 상황을 생각해보자.

두 빨간 칸 모두 백의 입장에서 착수할 경우 연결된 그룹이 흑돌로 둘러싸이게 되어 원래 바둑의 규칙에서는 백의 입장에서 스스로 잡히는 곳이지만 Baduk2에서는 이와 무관하게 백이 빨간 칸 두 곳에 착수해 8개의 흑돌이 들어있는 그룹의 돌을 죽일 수 있다.
저항군은 AI에게 Baduk2로 도전장을 내밀었고 AI는 의외로 순순히 도전을 받아들였다. 이제 저항군은 2116년 3월 9일, 인류의 자존심을 건 Baduk2 대결을 시작한다. 그리고 당신에게 인류의 승리를 돕기 위해 현재 판 위에서 돌 2개를 두어 상대 돌을 최대한 많이 죽이게끔 하는 프로그램을 작성하는 임무가 주어졌다. 인류의 명예를 걸고 현재 판이 주어질 때 돌 2개를 두어 죽일 수 있는 상대 돌의 최대 갯수를 구하는 프로그램을 작성하자.
입력
첫째 줄에 바둑판의 행의 갯수와 열의 갯수를 나타내는 N(3 ≤ N ≤ 20)과 M(3 ≤ M ≤ 20)이 한 칸의 빈칸을 사이에 두고 주어진다. 그 다음 N개의 줄에는 각 줄마다 배열의 각 행을 나타내는 M개의 정수가 한 개의 빈 칸을 사이에 두고 주어진다. 각 칸에 들어가는 값은 0, 1, 2이다. 0은 빈 칸, 1은 나의 돌, 2는 상대의 돌을 의미한다. 빈 칸이 2개 이상 존재함과 현재 바둑판에서 양 플레이어 모두 상대방의 돌로 빈틈없이 에워싸인 그룹이 없음이 모두 보장된다.
출력
첫째 줄에 현재 판에서 돌 2개를 두어 죽일 수 있는 상대 돌의 최대 갯수를 출력한다.
알고리즈: 브루트포스, BFS
풀이
N,M의 범위는 (3 <= N,M <= 20)로 바둑판의 최대 크기는 20x20이다. 20x20 바둑판에 2개의 돌을 놓는 경우의 수는 159600 (400 * 399)이다. 즉 브루트포스 풀이가 가능하다.
이제 각 경우의 수에서 2번 돌을 몇 개 먹을 수 있는지 확인한다. 모든 좌표를 돌면서 2번 돌이고, 확인하지 않은 돌이라면, 해당 그룹에 속한 모든 돌을 확인해보는데 이때 BFS 알고리즘을 활용한다. 각 돌의 상화좌우 중 한 곳이라도 0번이 존재한다면 그 돌이 속한 그룹은 먹을 수 없는 돌이다. 반대로 모든 돌의 상하좌우에 0번이 존재하지 않는다면, 그 그룹은 먹을 수 있는 돌이기 때문에 전체 카운터 변수에 더해준다.
소스 코드
import java.io.*;
import java.util.*;
class Coordinate {
int x,y;
Coordinate(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Main {
static int N,M;
static int board[][];
static final int dx[] = {-1, 0, 1, 0};
static final int dy[] = {0, -1, 0, 1};
static int ans = 0;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
board = new int[N][M];
for(int i=0; i<N; i++) {
StringTokenizer n_st = new StringTokenizer(br.readLine());
for(int j=0; j<M; j++) {
board[i][j] = Integer.parseInt(n_st.nextToken());
}
}
DFS(0);
System.out.println(ans);
}
static void DFS(int depth) {
if(depth == 2) {
ans = Math.max(ans, count_baduk());
return;
}
for(int i=0; i<N; i++) {
for(int j=0; j<M; j++) {
if(board[i][j]==0) {
board[i][j] = 1;
DFS(depth+1);
board[i][j] = 0;
}
}
}
}
static int count_baduk() {
int ac = 0; //전체 개수
boolean visited[][] = new boolean[N][M];
for(int i=0; i<N; i++) {
for(int j=0; j<M; j++) {
if(board[i][j] == 2 && !visited[i][j]) {
int c = 1;
boolean isPoss = true;
Queue<Coordinate> que = new LinkedList<>();
que.add(new Coordinate(j,i));
visited[i][j] = true;
while(que.size()!=0) {
Coordinate n = que.poll();
for(int k=0; k<4; k++) {
int nx = n.x + dx[k];
int ny = n.y + dy[k];
if((nx>=0 && nx<=M-1) && (ny>=0 && ny<=N-1)) {
if(board[ny][nx] == 2 && !visited[ny][nx]) {
que.add(new Coordinate(nx, ny));
c += 1;
visited[ny][nx] = true;
} else if(board[ny][nx] == 0) isPoss = false;
}
}
}
if(isPoss) ac += c;
}
}
}
return ac;
}
}