문제 링크
문제
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다. 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다.

초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다. 가로선은 인접한 두 세로선을 연결해야 한다. 단, 두 가로선이 연속하거나 서로 접하면 안 된다. 또, 가로선은 점선 위에 있어야 한다.
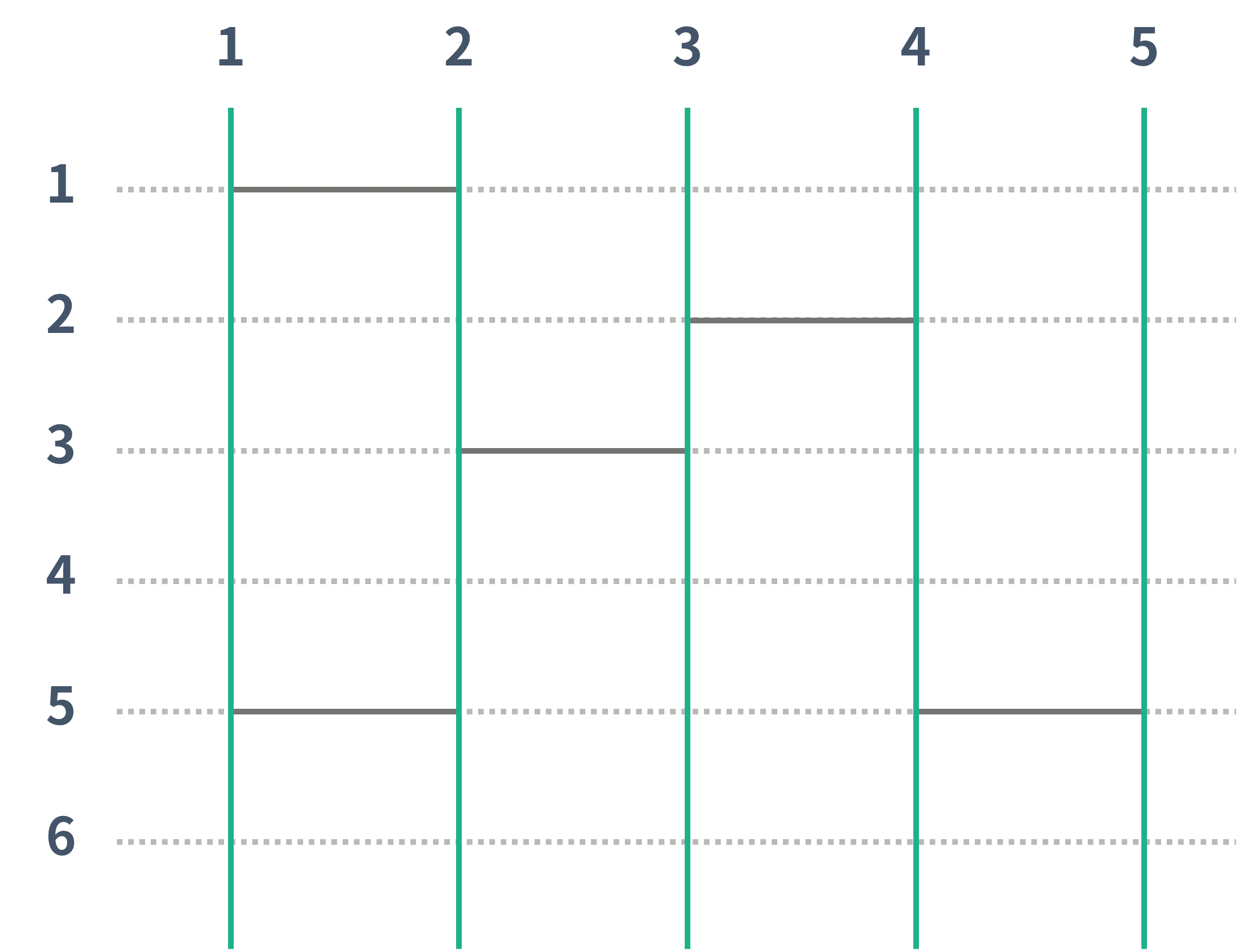
위의 그림에는 가로선이 총 5개 있다. 가로선은 위의 그림과 같이 인접한 두 세로선을 연결해야 하고, 가로선을 놓을 수 있는 위치를 연결해야 한다.
사다리 게임은 각각의 세로선마다 게임을 진행하고, 세로선의 가장 위에서부터 아래 방향으로 내려가야 한다. 이때, 가로선을 만나면 가로선을 이용해 옆 세로선으로 이동한 다음, 이동한 세로선에서 아래 방향으로 이동해야 한다.
위의 그림에서 1번은 3번으로, 2번은 2번으로, 3번은 5번으로, 4번은 1번으로, 5번은 4번으로 도착하게 된다. 아래 두 그림은 1번과 2번이 어떻게 이동했는지 나타내는 그림이다.
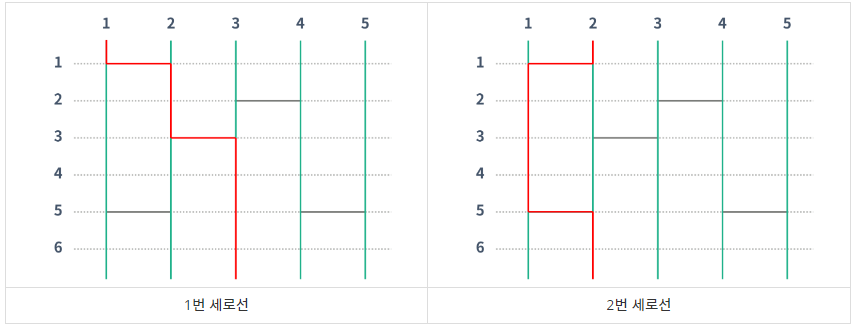
사다리에 가로선을 추가해서, 사다리 게임의 결과를 조작하려고 한다. 이때, i번 세로선의 결과가 i번이 나와야 한다. 그렇게 하기 위해서 추가해야 하는 가로선 개수의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 세로선의 개수 N, 가로선의 개수 M, 세로선마다 가로선을 놓을 수 있는 위치의 개수 H가 주어진다. (2 ≤ N ≤ 10, 1 ≤ H ≤ 30, 0 ≤ M ≤ (N-1)×H)
둘째 줄부터 M개의 줄에는 가로선의 정보가 한 줄에 하나씩 주어진다.
가로선의 정보는 두 정수 a과 b로 나타낸다. (1 ≤ a ≤ H, 1 ≤ b ≤ N-1) b번 세로선과 b+1번 세로선을 a번 점선 위치에서 연결했다는 의미이다.
가장 위에 있는 점선의 번호는 1번이고, 아래로 내려갈 때마다 1이 증가한다. 세로선은 가장 왼쪽에 있는 것의 번호가 1번이고, 오른쪽으로 갈 때마다 1이 증가한다.
입력으로 주어지는 가로선이 서로 연속하는 경우는 없다.
출력
i번 세로선의 결과가 i번이 나오도록 사다리 게임을 조작하려면, 추가해야 하는 가로선 개수의 최솟값을 출력한다. 만약, 정답이 3보다 큰 값이면 -1을 출력한다. 또, 불가능한 경우에도 -1을 출력한다.
알고리즘: 구현, 브루트포스, 백트래킹
풀이
세로선의 개수 N의 범위 (2 <= N <= 10), 가로선의 개수 H의 범위는 (1 <= H <= 30)이다.
최대 범위라고 할 때 N = 10, H = 30 가로선을 놓을 수 있는 위치는 9 30 = 총 270개다.
그리고 가로선은 최대 3개를 놓을 수 있다. 좌표를 고르는 순서는 중요하지 않기 때문에 270개 좌표 중에서 3개를 골라 조합하면 된다. 그러면 총 경우의 수는 약 300만(270! / 3! 267!)으로 모든 경우의 수를 고려하는 브루트 포스 알고리즘을 사용할 수 있다.
각 경우의 수에서 i번 세로선의 결과가 i번 나오는지 체크한다. 내가 구현한 방법은 boolean 2차원 배열을 두고 세로선 사이 각 통로에 high 별 가로선이 있는지 없는지 true, false로 표시해뒀다. 그리고 high = 1부터 H까지 line을 변경해가면서 H+1값이 되면 현재 line이 어디인지 확인했다. high이 한 칸 올라갈 때마다 탐색해야 할 가로선이 N개씩 줄어들기 때문에 최대 ((N-1)*H)/N번의 연산으로 i라인의 결과를 알 수 있다.
시간복잡도를 계산하면 위 계산대로라면 약 10억회 연산이 필요할 수 있다. 하지만 check()함수의 경우 매우 간단한 연산으로 구성돼 있기 때문에 충분히 위 방식으로 풀 수 있다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int N,M,H;
static boolean ladder[][];
static ArrayList<Integer> hLine_crd = new ArrayList<>(); //가로선 좌표
static int ans = -1;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
H = Integer.parseInt(st.nextToken());
ladder = new boolean[N][H+1];
for(int i=0; i<M; i++) {
StringTokenizer n_st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(n_st.nextToken());
int b = Integer.parseInt(n_st.nextToken());
ladder[b][a] = true;
}
for(int i=0; i<=3; i++) {
if(DFS(i)) {
ans = i;
break;
}
}
System.out.println(ans);
}
static boolean DFS(int nh) {
if(hLine_crd.size()==nh) {
if(check()) return true;
return false;
}
for(int i=1; i<N; i++) {
for(int j=1; j<=H; j++) {
int crd = i*100 + j;
if(hLine_crd.size()==0) {
if(!ladder[i][j]) {
hLine_crd.add(crd);
ladder[i][j] = true;
if(DFS(nh)) return true;
hLine_crd.remove(hLine_crd.size()-1);
ladder[i][j] = false;
}
} else {
if(hLine_crd.get(hLine_crd.size()-1) < crd && !ladder[i][j]) {
hLine_crd.add(crd);
ladder[i][j] = true;
if(DFS(nh)) return true;
hLine_crd.remove(hLine_crd.size()-1);
ladder[i][j] = false;
}
}
}
}
return false;
}
static boolean check() {
for(int i=1; i<=N; i++) {
int high = 0;
int line = i;
while(high<H) {
high += 1;
if(line == 1) {
if(ladder[line][high]) line = 2;
} else if(line == N) {
if(ladder[line-1][high]) line = line-1;
} else {
if(ladder[line-1][high]) line = line-1;
else if(ladder[line][high]) line = line+1;
}
}
if(i != line) return false;
}
return true;
}
}