문제 링크
문제
티어: 골드 2
알고리즘: 그리디, dp, 정렬

입력
첫째 줄에 n, m(1 ≤ n, m ≤ 1,000)이 주어진다. 다음 줄에는 n명의 남자들의 성격이 주어진다. 그 다음 줄에는 m명의 여자들의 성격이 주어진다. 성격은 1,000,000이하의 자연수이다.
출력
첫째 줄에 성격의 차이의 합의 최솟값을 출력한다.
풀이
성격의 차이의 합의 최솟값을 구하기 전에 n == m이라면 어떻게 최적해를 구할 수 있는지를 알아야 한다.
n == m인 경우에는 남자들의 성격과 여자들의 성격을 오름차순으로 정렬하고, 각 인덱스의 차이의 합이 최적해다.
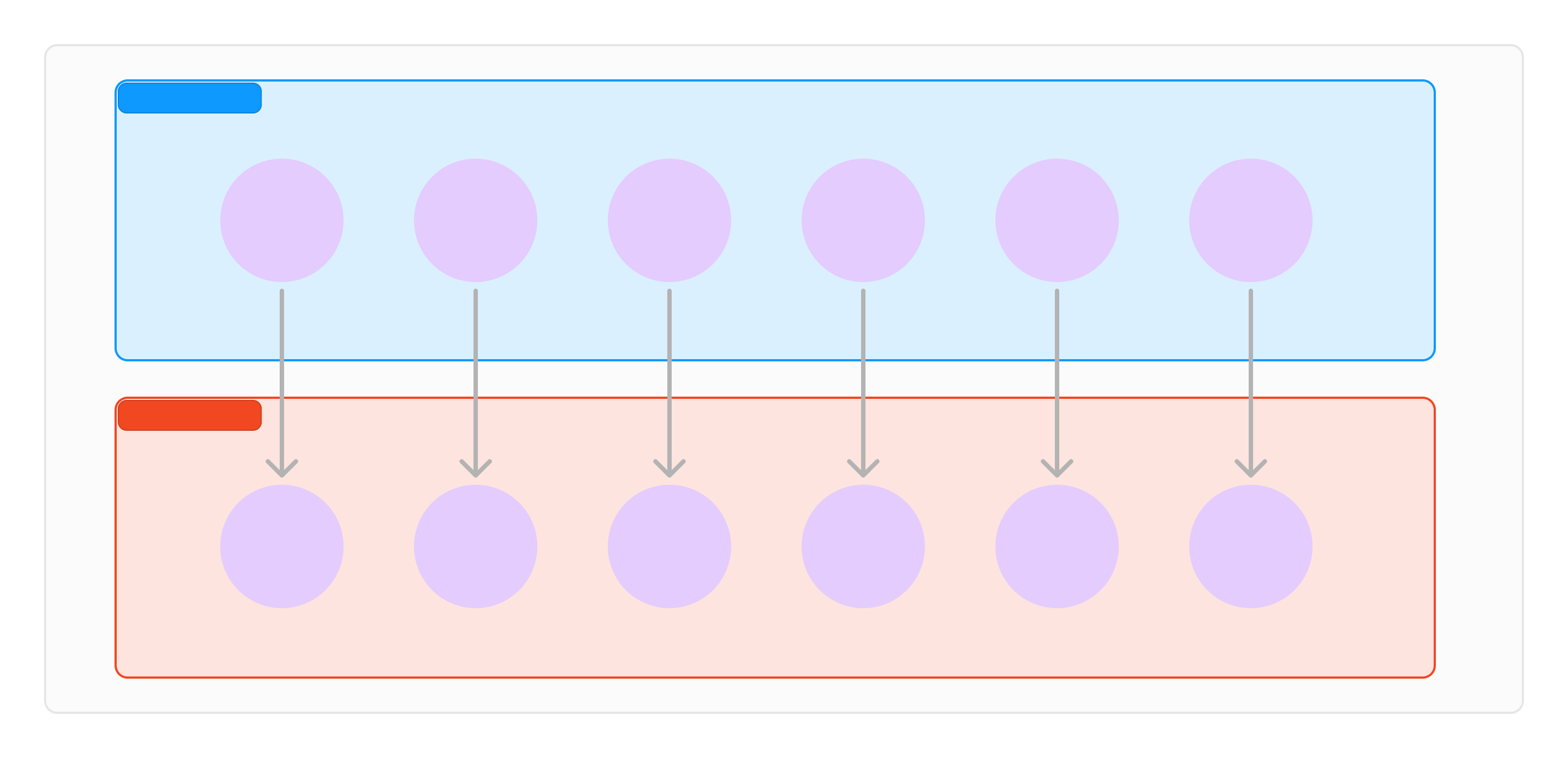
왜냐하면 각 배열은 증가하는 값을 가지고, 배열의 각 요소는 상대 배열의 요소 중 하나를 반드시 선택해야 되기 때문에 가장 작은 값은 가장 작은 값을 선택하고, 가장 큰 값은 가장 큰 값을 선택하는 것이 최선의 선택이 될 수밖에 없다.
그래서 우리는 먼저, 각 배열을 오름차순으로 정렬해 놓고 시작해야 된다.
문제에서는 n과 m은 다르기 때문에 이러한 경우는 어떻게 해야될까?
여기서 dp와 그리디가 사용된다.
dp[x][y]를 먼저 정의하자면, 남자 배열에서 x - 1번 째 인덱스까지와 여자 배열에서 y - 1번 째 인덱스까지의 최적해를 의미한다. 즉, 남자가 x명있고, 여자가 y명있을 때 최적해를 의미한다. (여기서 x명은 남자 배열에서 x - 1인덱스까지를 의미함 y도 같음)
그러니까 dp[1][1]인 경우는 남자 배열에서 0번 째 인덱스까지, 여자 배열에서 0번 째까지의 최적해인 것이다. 그래서 dp[1][1]은 그냥 Math.abs(male[0] - female[0])을 저장하면 된다.
그러면 바로 dp[2][2]부터 보면, 최적해는 dp[1][1] + Math.abs(male[1] - female[1])이 된다.
dp[2][3]의 경우는 여자 배열에서 새로운 인덱스가 포함되었기 때문에 새로 추가된 여자를 선택하는 경우와 그렇지 않은 경우로 나눠서 비교하면 된다.
-
새로 추가된 여자를 선택하는 경우
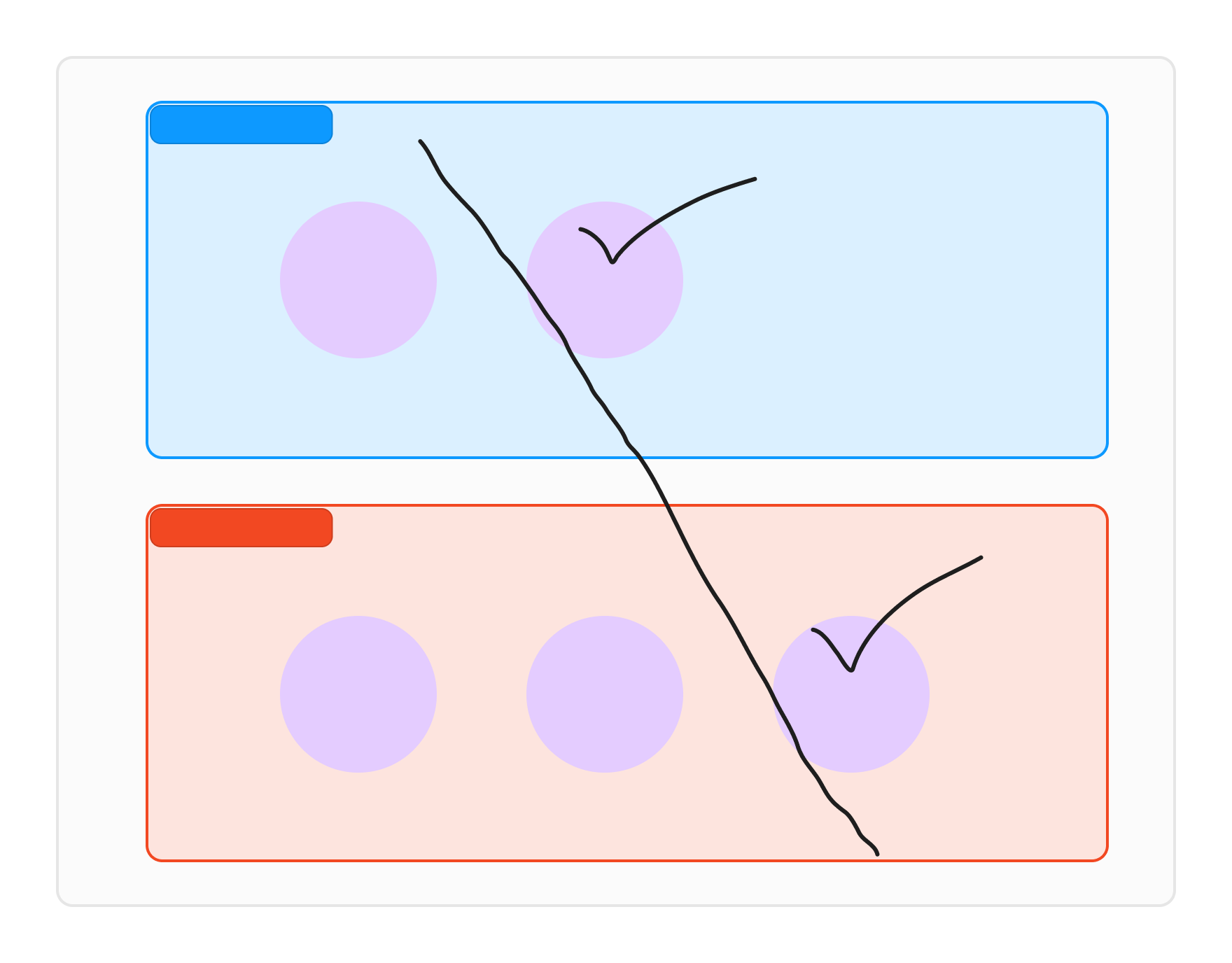
남자 배열에서 가장 마지막 요소와 이어주는게 최선의 선택이 된다. 이는 n == m 일 때 최적해를 구하는 논리와 정확히 같다.
그리고 나머지 남자 한명은 나머지 여자 두 명중 한명과 이어져야 한다.
이는 dp[1][2]에 해당한다.
그래서 새로 추가된 여자를 선택하는 경우는 dp[1][2] + Math.abs(male[1] - female[2])가 된다. -
새로 추가된 여자를 선택하지 않는 경우
이 경우는 dp[2][2]다.
이 두 값을 비교해서 더 작은 값이 최적해이기 때문에 그 값을 dp[2][3]에 저장하면 된다.
그래서 dp[n][m]까지 반복하면서 채워나가면 시간 복잡도 O(n * m)으로 풀 수 있다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int n,m;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
int dp[][] = new int[n + 1][m + 1];
for(int i=0; i<dp.length; i++) {
dp[i][0] = 0;
}
for(int i=0; i<dp[0].length; i++) {
dp[0][i] = 0;
}
int male[] = new int[n];
StringTokenizer st2 = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++) {
male[i] = Integer.parseInt(st2.nextToken());
}
int female[] = new int[m];
StringTokenizer st3 = new StringTokenizer(br.readLine());
for(int i=0; i<m; i++) {
female[i] = Integer.parseInt(st3.nextToken());
}
Arrays.sort(male);
Arrays.sort(female);
for(int i=1; i<=n; i++) {
for(int j=1; j<=m; j++) {
if(i == j) {
dp[i][j] = Math.abs(male[i - 1] - female[j - 1]) + dp[i - 1][j - 1];
} else if(i > j) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j - 1] + Math.abs(male[i - 1] - female[j - 1]));
} else {
//i < j
dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j - 1] + Math.abs(male[i - 1] - female[j - 1]));
}
}
}
System.out.println(dp[n][m]);
}
}