[백준 - 3086번] 초콜릿 자르기 - Java

문제 링크

https://www.acmicpc.net/problem/3086

문제

티어: 골드 1
알고리즘: dp

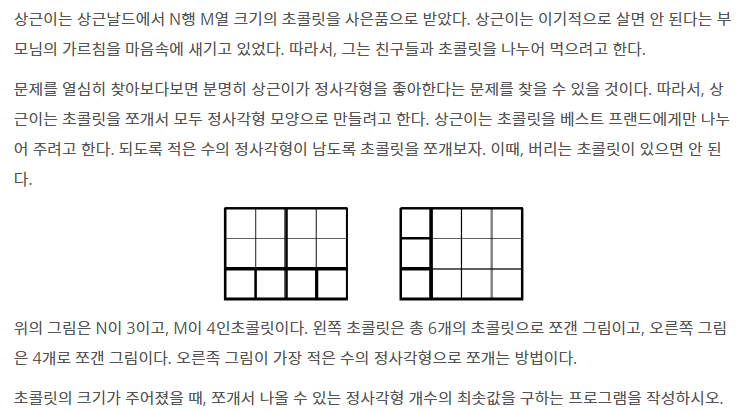
입력

첫째 줄에 N과 M이 주어진다. (1 ≤ N, M ≤ 1000)

출력

첫째 줄에 초콜릿을 쪼개서 나올 수 있는 정사각형 개수의 최솟값을 출력한다.

풀이

초킬릿을 쪼개서 나올 수 있는 정사각형 개수의 최솟값을 출력해야 한다.

처음 1x1 하나만 있을 때는 값은 1이다.
1x2이 경우는 2고,
..
1xN인 경우는 N이다.

여기서 행이 3인 시점부터 보면,

3x3는 1이고, (열과 행이 같다면 당연히 1이 최솟값이 된다.)
3x4부터는 전의 값을 활용해서 구할 수 있다.
먼저 케이스를 분류하면

• 새로 추가된 3x1을 3x3와 합치지 않는 경우
• 합치는 경우로 나눌 수 있다.

1. 합치지 않은 경우는 3x3 + 3x1이다.

2. 합친 경우는 합쳐질 수 있는 모든 경우를 따져봐야 한다. 그래서
   추가적으로 3x2 + 3x2의 값을 구해 비교하게 된다.
   만약 3x6를 구하는 경우는 3x4 + 3x2, 3x3 + 3x3을 추가적으로 따져본다. (반지점까지만)

그런데 여기서 끝나는 것이 아닌 아래 행이 추가되었다고 가정하고, 같은 방식을 적용해야 정확히 최솟값을 구할 수 있다.

예를 들어 6x5를 구하는 경우 5x5 + 1x5, 4x5 + 2x5, 3x5 + 3x5를 추가적으로 따져본다.

그래서 결과적으로 6x5의 최솟값을 구하게 되면, 5x6도 똑같기 때문에 같은 값으로 채워준다.

기존의 값을 활용해서 가능한 모든 경우를 구하는 것이기 때문에 풀이를 이해하는데 어렵지 않을 것이다.

이 풀이를 적용하면 dp는 dp[maxCol][maxRow]이다.

소스 코드

import java.io.*;
import java.util.*;

public class Main {
    static int N, M;
  public static void main(String args[]) throws IOException {
      BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
      StringTokenizer st = new StringTokenizer(br.readLine());
      N = Integer.parseInt(st.nextToken());
      M = Integer.parseInt(st.nextToken());
      int maxLen = Math.max(N, M);
      int[][] dp = new int[maxLen + 1][maxLen + 1];
      for(int i=1; i<=maxLen; i++) {
          dp[1][i] = i;
          dp[i][1] = i;
      }
      
      for(int i=2; i<=maxLen; i++) {
          for(int j=2; j<=maxLen; j++) {
              if(i == j) {
                  dp[i][j] = 1;
              } else {
                  if(dp[i][j] == 0) {
                      //열
                      dp[i][j] = dp[i][j - 1] + dp[i][1];
                      for(int k=2; k<=j/2; k++) {
                          dp[i][j] = Math.min(dp[i][j], dp[i][j - k] + dp[i][k]);
                      }
                      
                      //행
                      dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + dp[1][j]);
                      for(int k=2; k<=i/2; k++) {
                          dp[i][j] = Math.min(dp[i][j], dp[i - k][j] + dp[k][j]);
                      }
                      dp[j][i] = dp[i][j];
                  }
              }
          }
      }
      System.out.println(dp[N][M]);
  }
}