문제 링크
문제
티어: 골드 1
알고리즘: dp
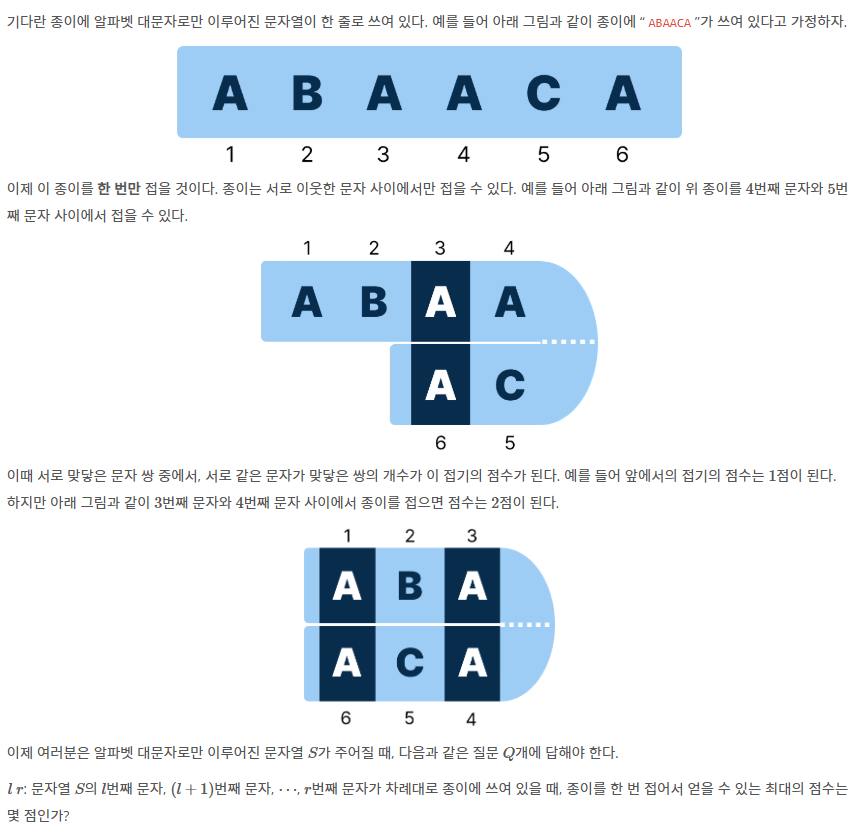
입력
첫 번째 줄에 문자열의 길이를 나타내는 정수 $ N $이 주어진다.
두 번째 줄에 알파벳 대문자로만 이루어진 문자열 $ S $가 주어진다.
세 번째 줄에 정수 $ Q $가 주어진다.
네 번째 줄부터 $ Q 개 줄에 걸쳐 위에서 설명한 질문을 나타내는 정수 $l, 이 공백으로 구분되어 주어진다.
출력
각 질문의 답을 나타내는 정수를 순서대로 한 줄에 하나씩 출력한다.
제한
-
$ 2 \le N \le 5{,}000 $
-
$ 1 \le Q \le 200{,}000 $
-
$ 1 \le l \lt r \le N $
풀이
구간이 주어졌을 때 종이를 한 번 접어서 얻을 수 있는 최대의 점수를 구해야 한다.
A B A A C / A
여기서 마지막 A가 매칭될 수 있는 부분을 생각해 보자,
A는 5 번째 C와 3 번째 A와 1 번재 A와 매칭될 수 있다.
이렇게 각 구간마다 매칭될 수 있는 모든 부분을 체크한다면, 시간 초과로 불가능할 것이다.
그래서 핵심은 이 부분을 줄여야 한다.
그런데 생각해보면, B A A C에서 C는 4번째 A와 매칭되고, 2번째 B와 매칭되었을 것이다.
그렇기 때문에 A B A A C / A에서는 첫 번째 A와 매칭하고, 나머지 B A A C가 매칭되었을 때 값을 더해주면 A B A A C A를 구할 수 있다.
그런데 여기서 구한 값은 첫 번째와 마지막이 매칭되었을 때의 값을 구한 것이다. 이는 소스 코드에 dp 배열에 해당한다.
즉, dp[1][6]은 1과 6이 매칭되었을 때의 값이며, dp[2][5]는 2와 5가 매칭되었을 때의 값이다.
우리가 구해줘야 할 값은 구간에서의 최대 점수이기 때문에 dp에 짝수로 된 모든 구간을 업데이트했다면,
이제 각 구간에서 최대 값을 구해주면 된다. 예를 들어 2 ~ 4의 최댓값은 dp[2][4], dp[1][3], dp[3][4] 중 최댓값이 들어간다.
이러한 값을 넣는 dp 배열은 소스 코드에 answerDp에 해당한다.
이후에는 2 ~ 5를 구한다면 dp[2][5], answerDp[2][4], answerDp[3][5]를 비교해야 된다.
왜냐하면 dp[2][4], dp[3][5]는 그 구간에서의 최댓값을 의미하지 않지만 answerDp는 그 구간에서의 최댓값을 의미하기 때문이다.
answerDp를 구했으면, 전처리 과정은 끝난 것이며, 구간 별 최댓값을 차례대로 출력해 주면 된다.
이 풀이의 시간 복잡도는 O(N^2)이 된다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int N, Q;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
String S = " " + br.readLine();
int[][] dp = new int[N + 1][N + 1]; //[l][r]
int[][] answerDp = new int[N + 1][N + 1];
for(int i=1; i<=N - 1; i++) {
if(S.charAt(i) == S.charAt(i + 1)) {
dp[i][i + 1] = 1;
answerDp[i][i + 1] = 1;
}
}
for(int k=4; k<=N; k++) {
//k는 구간의 길이를 뜻함. 구간 짝수 길이
for(int i=1; i<=N; i++) {
if(k % 2 == 1) {
//홀수 일때는 건너뛴다.
break;
}
int end = i + k - 1; //구간의 마지막 인덱스
if(end > N) {
//end가 넘으면 break;
break;
}
int v = 0;
if(S.charAt(i) == S.charAt(end)) {
v += 1;
}
dp[i][end] = v + dp[i + 1][end - 1];
}
}
for(int k=3; k<=N; k++) {
for(int i=1; i<=N; i++) {
int end = i + k - 1;
if(end > N) {
break;
}
answerDp[i][end] = dp[i][end];
answerDp[i][end] = Math.max(answerDp[i][end], answerDp[i + 1][end]);
answerDp[i][end] = Math.max(answerDp[i][end], answerDp[i][end - 1]);
}
}
StringBuilder sb = new StringBuilder();
Q = Integer.parseInt(br.readLine());
for(int t=0; t<Q; t++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
sb.append(answerDp[s][e]).append("\n");
}
System.out.println(sb.toString().trim());
}
}