[백준] 4902번 삼각형의 값 - Java

문제 링크

https://www.acmicpc.net/problem/4902

문제

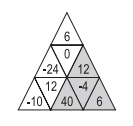
오른쪽 삼각형은 9개의 단위 삼각형이 총 3줄(N=3)로 이루어져 있다. 단위 삼각형은 N=1인 삼각형이다.

이때, 그림에서 서로 다른 부분 삼각형은 총 13개가 있다. (N=1인 삼각형이 9개, N=2인 삼각형이 3개, N=3인 삼각형이 1개)

N = 1인 경우 부분 삼각형은 1개, 2인 경우에는 5개, 3인 경우는 13개, 4인 경우는 27개가 있다.

이때, 단위 삼각형의 값을 삼각형 내부에 쓰여 있는 숫자의 값이라고 하자. 삼각형의 값은 삼각형 안에 있는 단위 삼각형의 값의 합이다.

오른쪽 그림은 가장 큰 값을 갖는 부분 삼각형이다.

삼각형이 주어졌을 때, 가장 큰 값을 갖는 부분 삼각형을 구하는 프로그램을 작성하시오.

입력

입력은 여러 개의 테스트 케이스로 이루어져 있고, 각 테스트 케이스는 한 줄로 이루어져 있다. 첫 번째 숫자는 줄의 수를 나타내고, 다음 숫자는 단위 삼각형에 적혀있는 값이 위에서 아래, 왼쪽에서 오른쪽 순서대로 주어진다. 마지막 줄에는 0이 주어진다.

줄의 개수는 400을 넘지 않으며, 단위 삼각형에 적혀있는 값의 절댓값은 1000을 넘지 않는다.

출력

각 테스트 케이스에 대해서, 테스트 케이스의 번호와 가장 큰 부분 삼각형의 값을 출력한다.

알고리즘: 구현, 브루트포스 누적 합

풀이

1줄을 높이 1이라 할 떄

높이가 1인 삼각형 좌표에서 삼각형은 N-y개 나온다.

높이가 1인 역삼각형 좌표에서 역삼각형은 그 좌표에서 나올 수 있는 가장 높은 역삼각형의 높이 만큼 나온다.

그래서 시간 복잡도를 계산해보면, 브루트 포스 풀이가 가능하다. 즉 모든 부분 삼각형을 찾아도 시간 초과 없이 풀이가 가능하다.

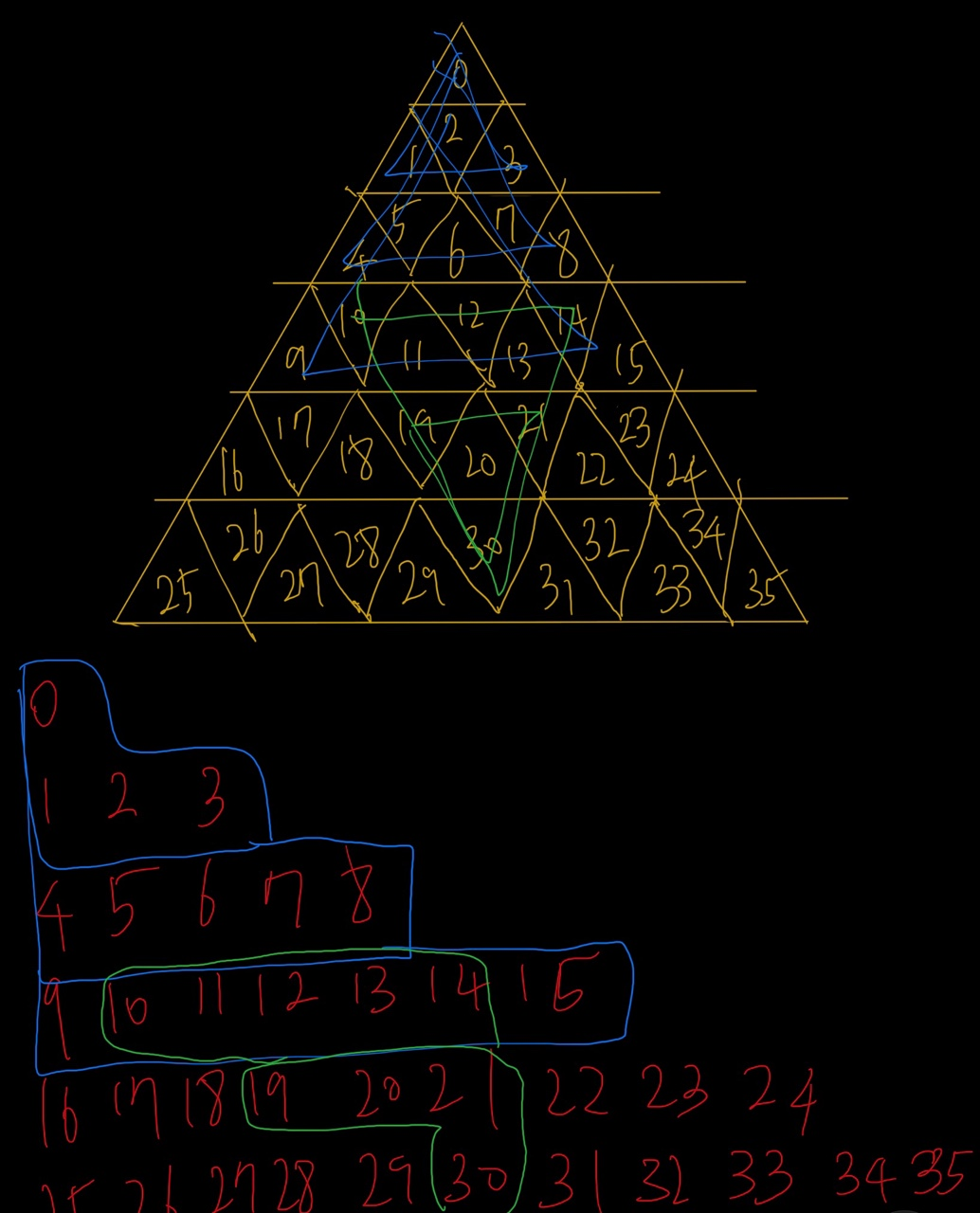
위 그림과 같이 나타낼 수 있는 모든 부분 정삼각형과, 역삼각형을 구해서 최댓값의 삼각형을 구하면 된다. 여기서 중요한 점은 triangle 2차원 배열에 값을 누적합으로 구성해야 한다.
그렇지 않으면 삼각형 값을 구하기 위해 많은 반복 횟수를 요구하기 때문에 시간 초과가 난다.

예를 들면 높이가 4인 삼각형 값을 구할 때 16번의 반복이 필요한데, 누적합을 이용하면 총 4번만으로 삼각형 값을 구할 수 있다. 이런식으로 누적합을 이용해서 반복 횟수를 획기적으로 줄여야 모든 부분 삼각형, 역삼각형의 값을 시간 초과 없이 구할 수 있다.

소스 코드

import java.io.*;
import java.util.*;

class Coordinate {
    int x, y;
    Coordinate(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

public class Main {
    static int N;
    static ArrayList <ArrayList<Long>> sum_triangle = new ArrayList<>();
    static long ans = -320000000;
    static int count = 1;
    static StringBuilder sb = new StringBuilder();
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        while(true) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            N = Integer.parseInt(st.nextToken());
            if(N == 0) break;
            sum_triangle = new ArrayList<>();
            ans = -320000000;
            for (int i = 0; i < N; i++) sum_triangle.add(new ArrayList<>());
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < 1 + i * 2; j++) {
                    if(j==0) sum_triangle.get(i).add(Long.parseLong(st.nextToken()));
                    else sum_triangle.get(i).add(sum_triangle.get(i).get(j-1) + Long.parseLong(st.nextToken()));
                }
            }
            for (int i = 0; i < N; i++) {
                for (int j = 0; j < sum_triangle.get(i).size(); j++) {
                    if (j % 2 == 0) {
                        //짝수면 부분 삼가형 찾기
                        find_triangle(new Coordinate(j, i));
                    } else {
                        //홀수면 부분 역삼각형 찾기
                        find_inverted_triangle(new Coordinate(j, i));
                    }
                }
            }
            sb.append(String.valueOf(count) + ". " + String.valueOf(ans) + "\n");
            count += 1;
        }
        System.out.println(sb.toString().trim());
    }

    static void find_triangle(Coordinate c) {
        long sum = 0;
        for (int i = c.y; i < N; i++) {
            if(c.x == 0) sum += sum_triangle.get(i).get(c.x + (i - c.y) * 2);
            else sum += sum_triangle.get(i).get(c.x + (i - c.y) * 2) - sum_triangle.get(i).get(c.x-1);
            ans = Math.max(ans, sum);
        }
    }

    static void find_inverted_triangle(Coordinate c) {
        long sum = 0;
        int rc = 0;
        while (true) {
            if(c.x-(rc * 2) == 0) sum += sum_triangle.get(c.y-rc).get(c.x);
            else sum += sum_triangle.get(c.y-rc).get(c.x) - sum_triangle.get(c.y-rc).get(c.x-(rc * 2)-1);
            rc += 1;
            ans = Math.max(ans, sum);
            if ((c.x + 1 - (1 + rc * 2)) < 0 || c.x == sum_triangle.get(c.y - rc).size()) break;
        }
    }
}