문제 링크
문제
티어: 골드 1
알고리즘: dp
선영이는 다양한 크기의 책을 쌓아서 스택 형태로 보관한다. 이런 스택의 가장 위에서부터 크기가 감소하지 않는 순서로 책이 쌓여져 있다면, 스택이 안정된 상태라고 한다. 그렇지 않은 경우에는 스택이 무너질 수도 있다.
선영이는 책이 무너지는 것을 막기 위해서 크기 순으로 스택을 정렬하려고 한다. 선영이는 스택의 중간 (또는 바닥)에서 책을 하나 뺀 다음, 가장 위에 놓는다. 하지만, 빼려고 하는 책의 위에 있는 스택이 안정된 상태이어야 한다.
아래 그림은 3, 4, 1, 2로 쌓여진 책을 크기 순으로 정렬하는 방법이다.
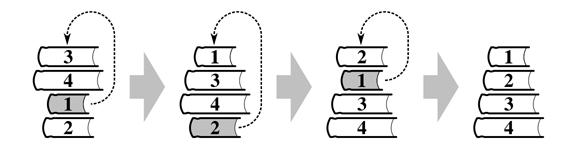
현재 책이 쌓여져 있는 상태가 입력으로 주어졌을 때, 안정된 상태로 책을 쌓기 위해 최소 몇 단계가 필요한지 구하는 프로그램을 작성하시오. 위의 그림의 경우에 답은 3이다.
입력
첫째 줄에 테스트 케이스의 개수가 주어진다. 테스트 케이스의 수는 100보다 작거나 같다.
각 테스트 케이스의 첫째 줄에는 책의 수 n이 주어진다. (1 ≤ n ≤ 50) 다음 줄에는 책의 크기 si가 스택의 맨 위에서부터 순서대로 주어진다. (1 ≤ si ≤ 1000)
출력
각 테스트 케이스에 대해서, 필요한 단계의 수의 최솟값을 출력한다.
풀이
안정된 상태로 책을 쌓기 위해 최소 몇 단계가 필요한지 구해야 한다.
일단 책을 위로 올릴 수 있는 경우는 위에가 정렬된 상태에서만 가능하기 때문에 정렬된 상태 다음이 작은지를 중점적으로 봐야 한다.
그래서 3 4 다음 1은 4보다 작기 때문에 1은 무조건 올려야 하는 책이 된다.
다음 예제를 보자,
8
3 1 4 1 5 9 2 6
여기서 1 1 2 3 4 5 9에서 다음은 6이고, 9보다 작기 때문에 맨 위로 올려줘야 한다.
-
(6) 1 1 2 3 4 5 9 여기서 6은 어디에 위치해야 될까? 인덱스 7에 존재해야 한다. (5 뒤)
즉, 인덱스 0부터 7까지 6이 이동해야 되는 것이다. -
일단 6이 인덱스 2까지 이동하면 1 1 6 2 3 4 5 9가 되고, 다음은 2가 올라가게 된다.
-
(2) 1 1 6 3 4 5 9 이번에 2는 어디에 위치해야 될까? 인덱스 2에 위치해야 된다. 생각해 보면, 이 값은 이미 구했다. 6이 맨 위에 있을 때 인덱스 2까지 가는 과정을 한 번 했기 때문에 이 값을 그대로 활용하면 된다. 그러면 6이 맨 위에 위치하고, 인덱스 2까지 가는 과정은 총 3회이기 때문에 2 또한 맨 위로 올라가고, 인덱스 2까지 가는 과정이 총 3회가 된다.
-
1 1 2 6 3 4 5 9 이번에는 3이 올라가게 되고, |(3) 1 1 2 6 3 4 5 9| 3은 인덱스 3에 위치해야 된다. (2 뒤) 그런데 이 값도 이미 구했다. 6이 맨위로 올라가고, 인덱스 3까지 가는 과정이기 때문에 이 과정은 (6 -> 인덱스 2까지 가는 과정 + 2가 인덱스 2까지 가는 과정)의 합이 된다.
..그래서 일반화하면, 다음과 같다.
특정 값이 맨 위로 올라가고, 어떤 인덱스에 위치해야 된다면, 2 * (삽입해야 될 위치 - 1 까지의 횟수)가 된다.
그래서 (삽입해야 될 위치 - 1 까지의 횟수)이 값을 dp로 저장해서, 활용한다면, 시간 초과없이 문제를 풀 수 있다.
dp[A] -> A는 최대 50까지 가진다. 만약 dp[3]이라면 인덱스 3에 삽입하는 데 필요한 최소 횟수를 의미한다.
여기서 중요한 점은 중복 값이 존재하는 경우다. 중복 값이 들어가게 되면, 결국 dp에 값은 정확한 값이 아니게 된다.
예를 들어 1 1 2 6에서 인덱스 3에 들어가는 횟수와 1 1 1 1에서 인덱스 3에 들어가는 횟수는 다르다. (만약 모든 책이 고유한 값이 였다면, 위 풀이로 끝났을 것이다.)
그래서 특정 값을 맨 위로 올리고 나서, 정렬을 하고, dp를 업데이트 하는 과정을 거쳐야 한다.
예를 들어 (2) 1 1 2 6 7에서 2는 dp[2]에 들어가기 때문에 answer에 dp[2]를 더하고, 그 이후 값인 dp[3], dp[4], dp[5]를 업데이트 해줘야 한다.
1 1 2 2 6 7 여기서 dp[3]은 고려해 주지 않아도 된다. 왜냐하면 2의 중간 위치이기 때문에 이 위치에 들어오는 경우는 없기 때문이다.
그래서 업데이트해 줘야 될 dp[4]를 보면, 인덱스 2에 도착하고, 2를 두 번 올리는 데 그 두 번 다 인덱스 2에 위치시켜야 한다.
그래서 이를 공식화하면 dp[4] = (붙어있는 2의 개수 + 1) * dp[4 - 붙어있는 2의 개수]가 된다.
정리하면, 정렬된 상태 바로 밑에 책을 어떤 위치에 삽입해야 하는지 구하고, 그 위치에 삽입 한 뒤 dp[insertInd]를 answer에 더해준다. 그리고 새롭게 정렬된 상태를 통해서 dp를 업데이트 해 나간다.
이 과정을 반복해서 모든 책이 정렬된 상태가 된다면, answer이 책을 쌓기 위한 최소 단계가 되는 것이다.
이 풀이의 시간 복잡도는 약 O(N^2)이다.
소스 코드
import java.io.*;
import java.util.*;
public class Main {
static int T;
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
T = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for(int t=0; t<T; t++) {
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
long[] dp = new long[N];
dp[0] = 1;
ArrayList<Integer> list = new ArrayList<>();
list.add(arr[0]);
long answer = 0;
int cntSame = 1;
for(int i=1; i<N; i++) {
int bottom = list.get(list.size() - 1);
if(bottom == arr[i]) {
list.add(arr[i]);
cntSame += 1;
} else if(bottom < arr[i]) {
list.add(arr[i]);
dp[i] = (cntSame + 1) * dp[i - cntSame];
cntSame = 1;
} else {
//bottom > arr[i] 올려야 될 값임. 1 2 3 4 5 -> 다음 4값이 온 것임
int insertInd = findInsertIndex(arr[i], list);
answer += dp[insertInd];
//다음에는 업데이트 해야됨.
list.add(arr[i]);
Collections.sort(list);
int cntSame2 = 1;
for(int j=insertInd + 1; j<=i; j++) {
int back = list.get(j - 1);
int cur = list.get(j);
if(back == cur) {
cntSame2 += 1;
} else if(back < cur) {
dp[j] = (cntSame2 + 1) * dp[j - cntSame2]; //업데이트
cntSame2 = 1;
}
}
}
}
sb.append(answer).append("\n");
}
System.out.println(sb.toString().trim());
}
static int findInsertIndex(int std, ArrayList<Integer> list) {
int result = -1;
for(int i=0; i<list.size(); i++) {
if(std <= list.get(i)) {
result = i;
break;
}
}
return result;
}
}