[프로그래머스] 두 원 사이의 정수 쌍 - Java

문제 링크

https://school.programmers.co.kr/learn/courses/30/lessons/181187

문제 설명

x축과 y축으로 이루어진 2차원 직교 좌표계에 중심이 원점인 서로 다른 크기의 원이 두 개 주어집니다. 반지름을 나타내는 두 정수 r1, r2가 매개변수로 주어질 때, 두 원 사이의 공간에 x좌표와 y좌표가 모두 정수인 점의 개수를 return하도록 solution 함수를 완성해주세요.
※ 각 원 위의 점도 포함하여 셉니다.

제한 사항

• 1 <= r1 < r2 <= 1,000,000

알고리즘: 수학

풀이

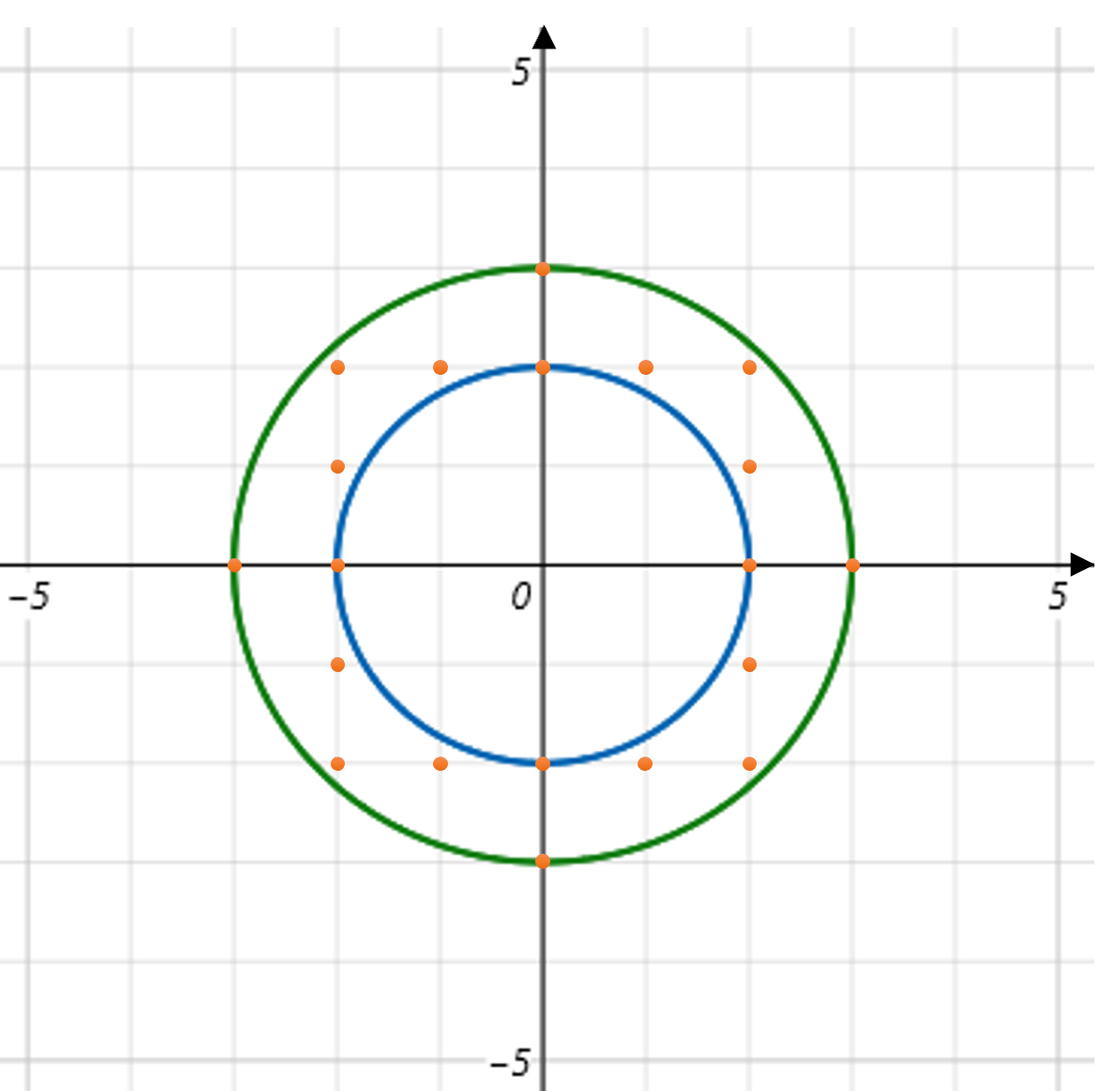
간단한 수학 공식만 알면 풀 수 있는 문제다. 원의 y좌표만 알면 모든 점을 구할 수 있다.
y좌표를 알기 위해서는 r^2 = x^2 + y^2이 공식을 이용하면 된다.

ex) r2의 반지름을 가진 원의 경우
x가 0일 때 y는 위 공식에 의해서 3이다.
x가 1일 때 y는 위 공식에 의해서 2루트2다. -> 2.xx
x가 2일 때 y는 위 공식에 의해서 루트5다. -> 2.xx
...

소스 코드

class Solution {
    public long solution(int r1, int r2) {
        long answer = 0;
        long cm_p = 0;
        for(int i=0; i<r1; i++) {
            double d_y1 = Math.sqrt(Math.pow(r1, 2) - Math.pow(i, 2));
            long y1 = (long) d_y1;
            if(d_y1 % 1 != 0) y1 += 1;
            long y2 = (long) Math.sqrt(Math.pow(r2, 2) - Math.pow(i, 2));   
            if(i == 0) cm_p = (y2 - y1 + 1) * 4;
            else answer += (y2 - y1) + 1;
        }
        for(int i=r1; i<r2; i++) answer += (long) Math.sqrt(Math.pow(r2, 2) - Math.pow(i, 2));
        answer *= 4;
        answer += cm_p;
        return answer;
    }
}