[프로그래머스] 숫자 카드 나누기 - Java

문제 링크

https://school.programmers.co.kr/learn/courses/30/lessons/135807

문제 설명

철수와 영희는 선생님으로부터 숫자가 하나씩 적힌 카드들을 절반씩 나눠서 가진 후, 다음 두 조건 중 하나를 만족하는 가장 큰 양의 정수 a의 값을 구하려고 합니다.

1. 철수가 가진 카드들에 적힌 모든 숫자를 나눌 수 있고 영희가 가진 카드들에 적힌 모든 숫자들 중 하나도 나눌 수 없는 양의 정수 a

2. 영희가 가진 카드들에 적힌 모든 숫자를 나눌 수 있고, 철수가 가진 카드들에 적힌 모든 숫자들 중 하나도 나눌 수 없는 양의 정수 a

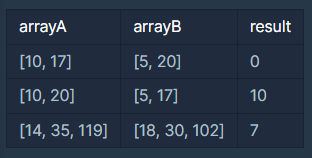
예를 들어, 카드들에 10, 5, 20, 17이 적혀 있는 경우에 대해 생각해 봅시다. 만약, 철수가 [10, 17]이 적힌 카드를 갖고, 영희가 [5, 20]이 적힌 카드를 갖는다면 두 조건 중 하나를 만족하는 양의 정수 a는 존재하지 않습니다. 하지만, 철수가 [10, 20]이 적힌 카드를 갖고, 영희가 [5, 17]이 적힌 카드를 갖는다면, 철수가 가진 카드들의 숫자는 모두 10으로 나눌 수 있고, 영희가 가진 카드들의 숫자는 모두 10으로 나눌 수 없습니다. 따라서 철수와 영희는 각각 [10, 20]이 적힌 카드, [5, 17]이 적힌 카드로 나눠 가졌다면 조건에 해당하는 양의 정수 a는 10이 됩니다.

철수가 가진 카드에 적힌 숫자들을 나타내는 정수 배열 arrayA와 영희가 가진 카드에 적힌 숫자들을 나타내는 정수 배열 arrayB가 주어졌을 때, 주어진 조건을 만족하는 가장 큰 양의 정수 a를 return하도록 solution 함수를 완성해 주세요. 만약, 조건을 만족하는 a가 없다면, 0을 return 해 주세요.

제한사항

알고리즘: 유클리드 호제법

풀이

먼저 arrayA에서 최대 공약수를 구하고, arrayB에서 최대 공약수를 구한다. -> 유클리드 호제법
arrayA의 최대 공약수를 GCD_A, arrayB의 최대 공약수를 GCD_B라고 하겠다.
arrayB의 요소 중 GCD_A로 나눌 수 있는 요소가 존재한다면, GCD_A는 답이 될 수 없다. 최대 공약수이기 때문에 최대 공약수가 나눌 수 있는 요소는 최대 공약수의 모든 공약수도 나눠지기 때문이다.
이러한 방법으로 GCD_A와 GCD_B가 답이 될 수 있는지 판단한다. 둘 다 답이 될 수 있다면 더 큰 값이 정답이고, 둘 다 답이 될 수 없다면, 0을 출력하면 된다.

소스 코드

class Solution {
    public int solution(int[] arrayA, int[] arrayB) {
        int answer = 0;
        int GCD_A = arrayA[0];
        int GCD_B = arrayB[0];
        for(int i=1; i<arrayA.length; i++) GCD_A = GCD(GCD_A, arrayA[i]);
        for(int i=1; i<arrayB.length; i++) GCD_B = GCD(GCD_B, arrayB[i]);
        answer = Math.max(check(arrayA, GCD_B), check(arrayB, GCD_A));
        return answer;
    }
    static int GCD(int x, int y) {
        if(y == 0) return x;
        else return GCD(y, x % y);
    }
    static int check(int[] array, int GCD) {
        for(int i=0 ;i<array.length; i++) {
            if(array[i] % GCD == 0) return 0;
        }
        return GCD;
    }
}