Multi-Label Image Recognition with Graph Convolutional Networks 리뷰

Paper : Multi-Label Image Recognition with Graph Convolutional Networks (Zhao-Min Chen, Xiu-Shen Wei, Peng Wang, Yanwen Guo / CVPR 2019)

Motivation

1. Graph Convolution Network에 대한 이해
2. Label dependency를 고려한 classification network 고찰

Overview

Multi-label image recognition task는 이미지 내에 있는 다양한 object를 예측하는 것이다. 한 이미지 내부에도 여러 object가 같이 나타나므로, 나타날 수 있는 object label 사이의 dependency 정보를 네트워크에 주입시키는 것은 매우 효과적일 것이다.

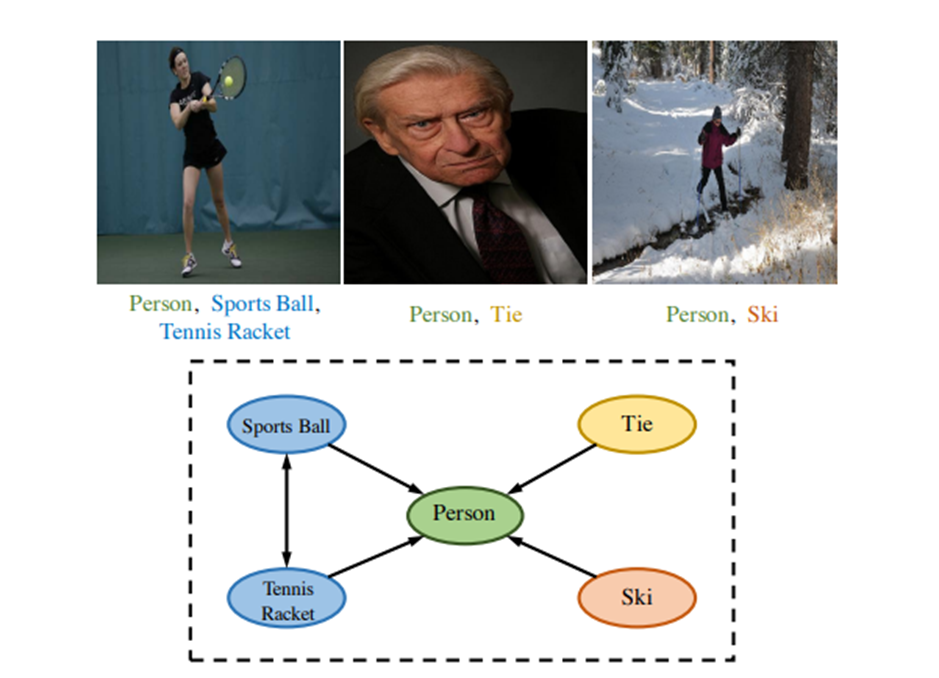
예를 들어서, "Tie"나 "Ski"가 이미지 내부에 있다면, "Person"도 이미지에 있을 확률이 상당히 높다. (물론 반대 방향은 아님)

이 논문에서는 이러한 label dependency를 Graph Convolution Network를 이용하여 design하는데, graph의 노드를 label의 word embedding로 사용하고, 최종 graph node feature를 각 object의 classifier로 사용한다.

원래 multi-label classification에서 각 label에 대한 classifier (i.e., 1x1 conv)가 independent한 parameter를 갖는 반면에 GCN을 통해 학습된 classifier는 각 object 사이의 관계를 잘 알고 있으므로, 더욱 좋은 성능을 낼 수 있게 된다.

이 classifier는 image feature extracter에 적용되어서 최종적으로 multi-label image recognition을 수행하게 된다.

Graph Convolutional Network

그림 출처: https://www.youtube.com/watch?v=YL1jGgcY78U

간단하게 GCN이 어떻게 작동하는지를 알아보자.

Graph data structure는 아래와 같이 Edge와 Vertices로 정의되며,

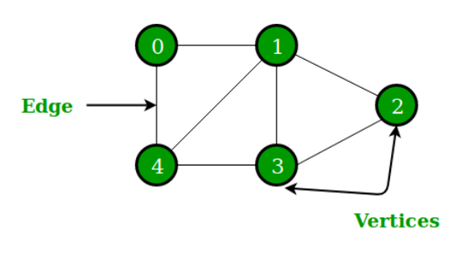
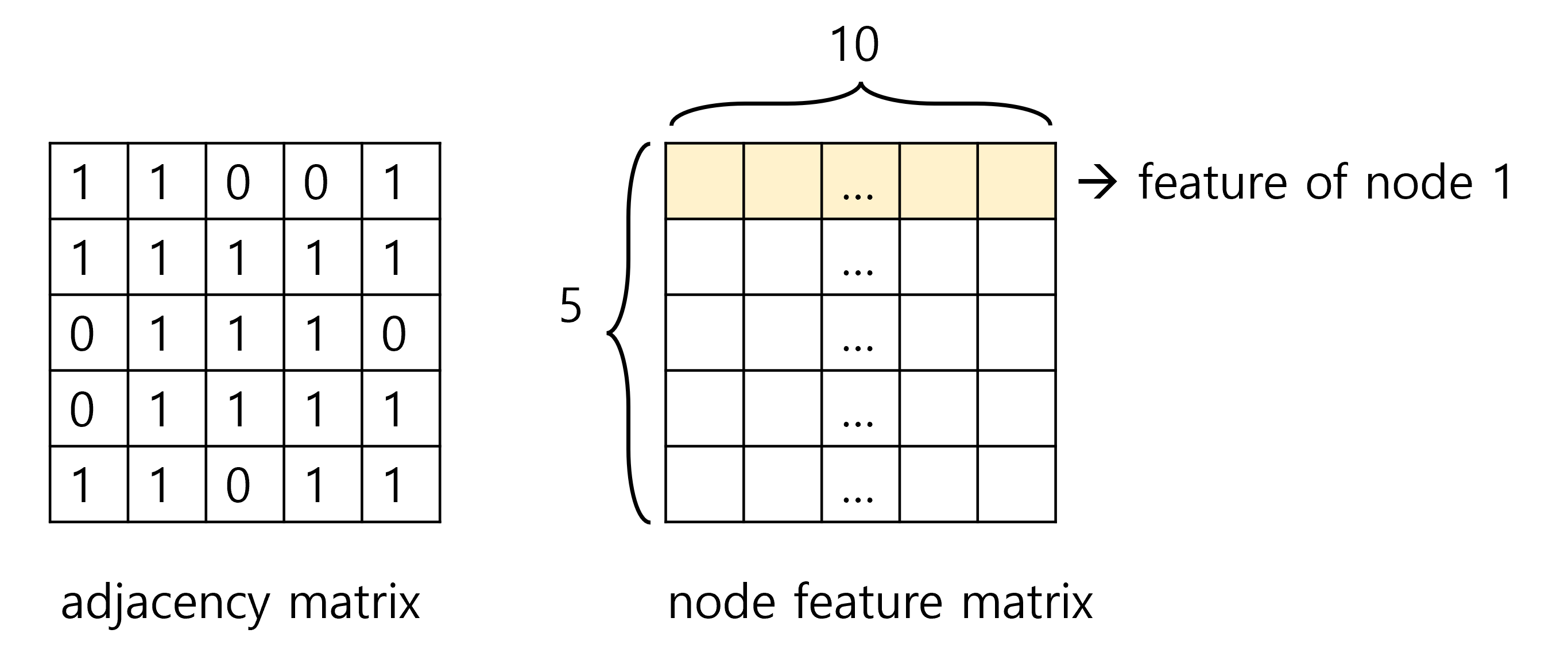
이를 표현하기 위해서는 각 node (vertex)가 어떤 node와 연결되어 있는지를 표현하는 adjacency matrix와 각 node feature를 표현하는 node feature matrix를 사용한다. (예: 5개의 노드, 각 feature 길이 10)

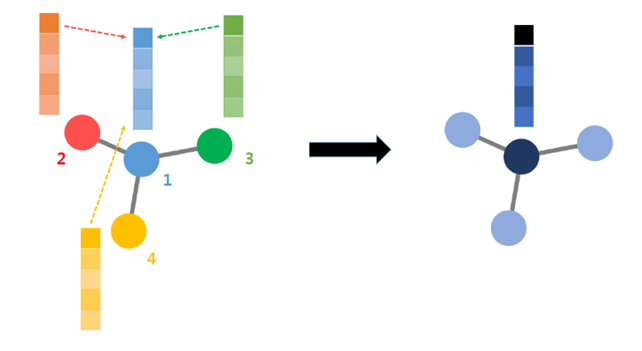
이렇게 데이터가 정의되면, CNN의 convolution처럼 parameter를 share하는 weight가 곱해지면서 다음 layer의 feature matrix를 만들어낸다. (아래 그림 출처: https://www.youtube.com/watch?v=YL1jGgcY78U)

여기서 $l$은 layer이고, $A$는 adjacency matrix, $H$는 node feature이다.
특히, $A$가 곱해지면서 각 node는 인접한 node feature들의 weighted sum으로 생각될 수 있고, 이는 관련이 있는 feature만 고려한다는 것이다.

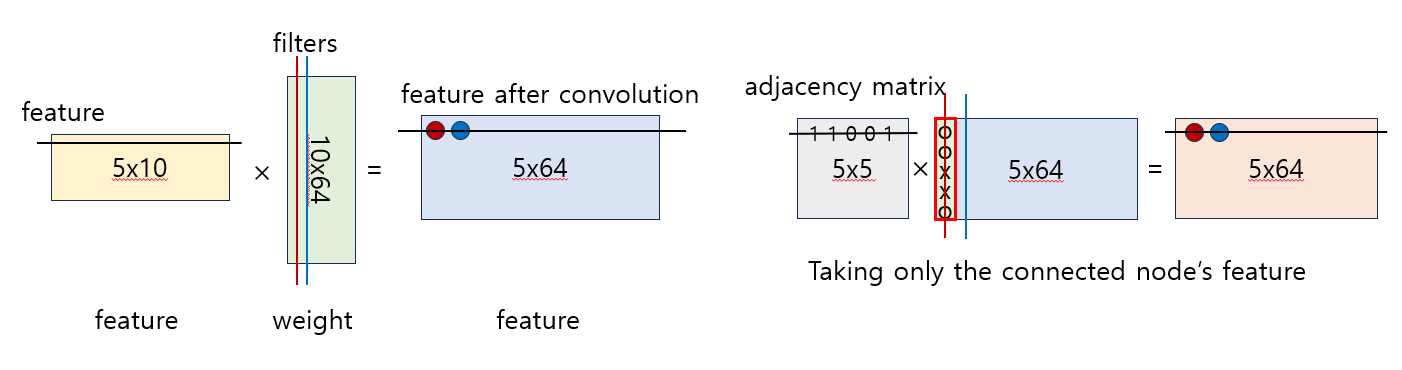
처음에 data structure를 이용하여 feature를 추출하는 과정을 살펴보면 위의 그림과 같이 그릴 수 있겠다. (initial feature = 10 / intermediate feature = 64로 가정)

Method

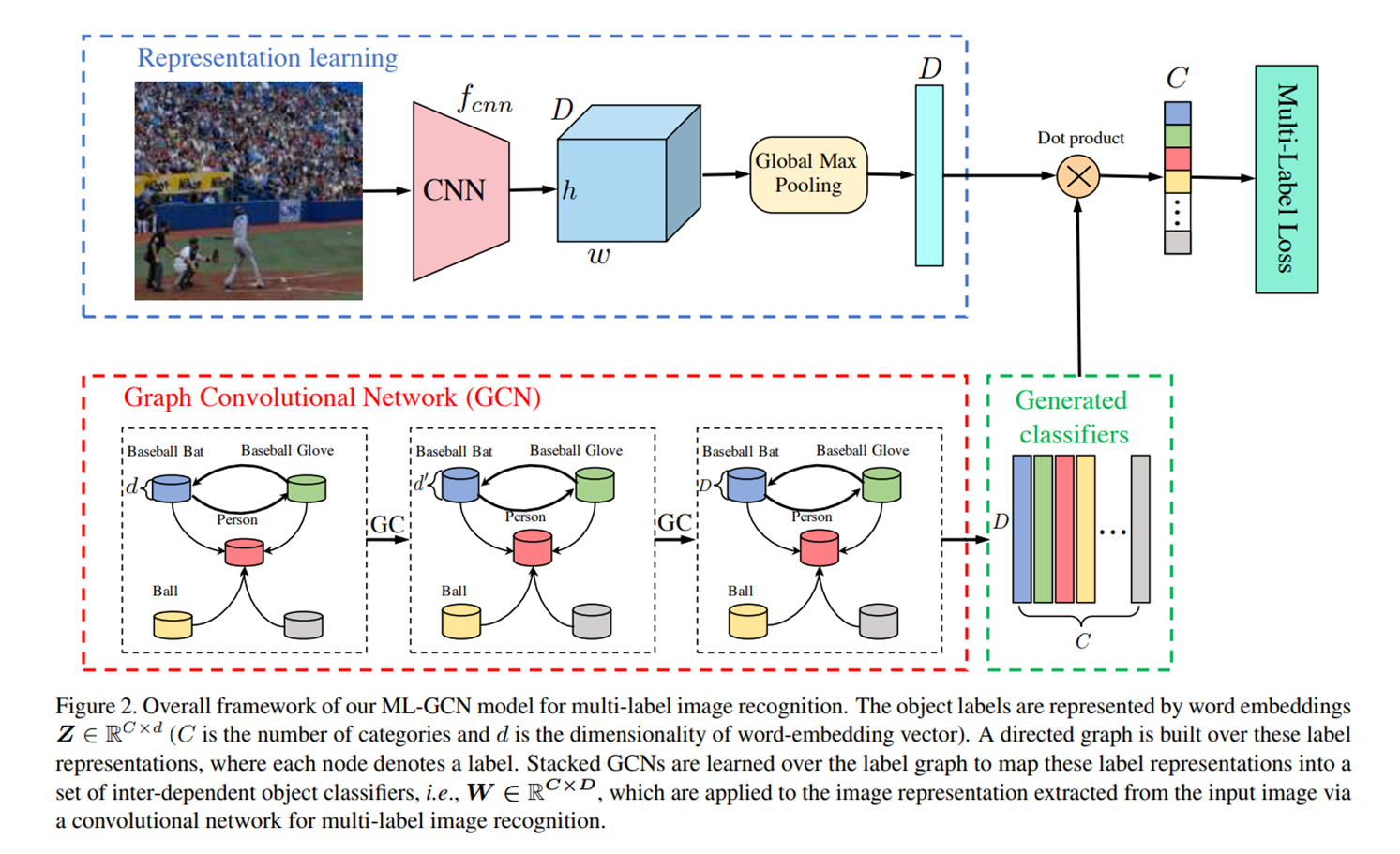
위의 그림은 Multi Label GCN의 overall architecture로 image representation learning 파트와 GCN 파트로 나뉘어 있으며, GCN에서 생성된 classifier를 이용해 image를 분류한다.

먼저, iamge representation learning 파트는 그냥 CNN base model을 image feature extractor로 사용한다. 그리고 최종 feature를 $D=2048$이 되도록 pooling한다.

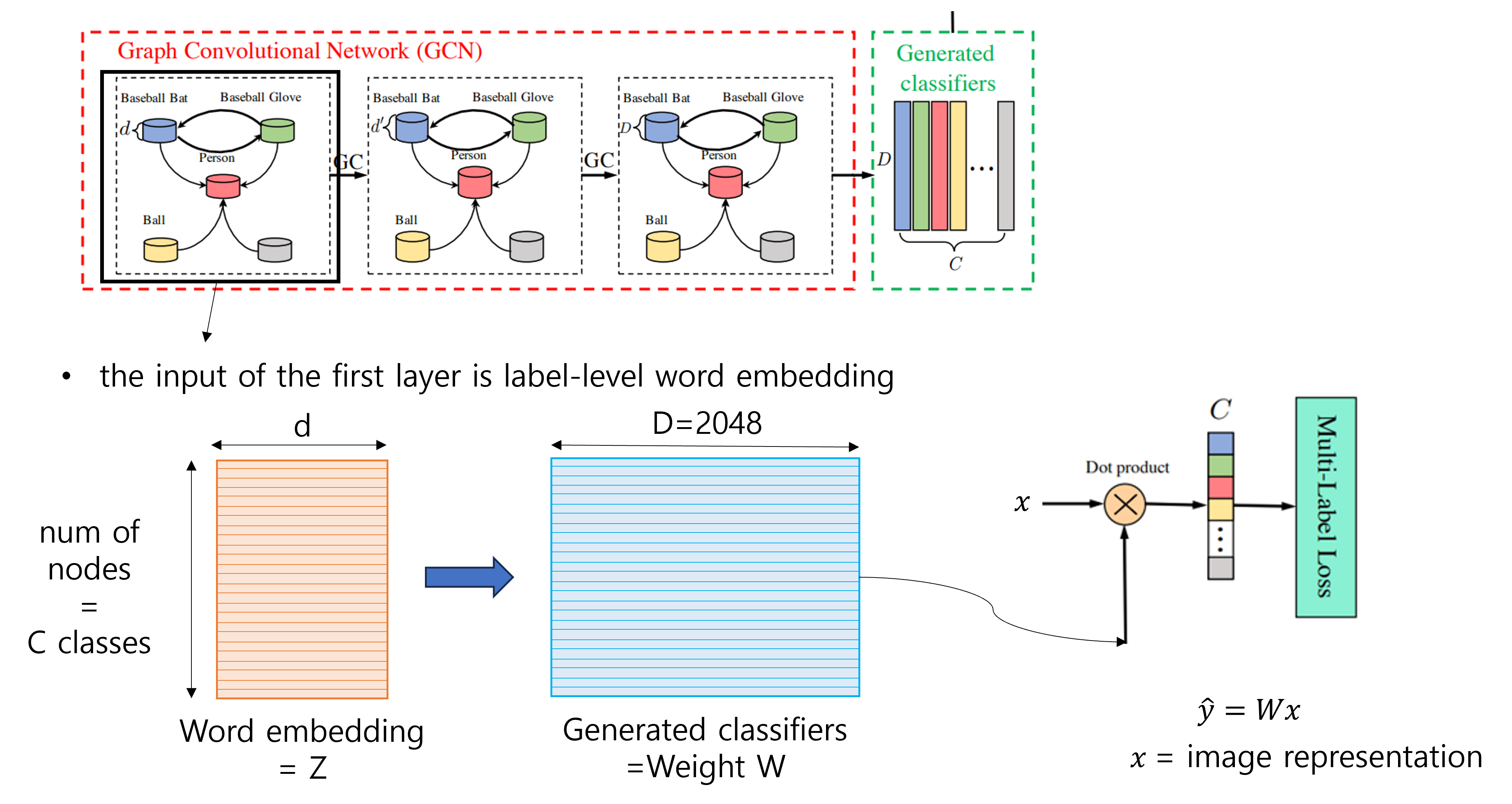
GCN 파트에서는 먼저, 미리 정의된 $C$개의 class label의 word embedding을 input으로 하여, GCN을 통과하면서 이미지와 똑같은 $D=2048$의 feature vector를 생성해낸다. 그러면 각 class마다 하나의 vector가 주어지는 것인데, 이 feature vector를 바로 각 class의 image classifier로 사용한다.

Correlation Matrix

GCN을 학습하기 위해서는 보통 pre-defined된 adjacency matrix (correlation matrix)가 필요하다. 하지만 우리와 같이 multi-label classification을 하는 경우, 이를 먼저 알 수가 없으므로, data-driven way로 학습을 한다.

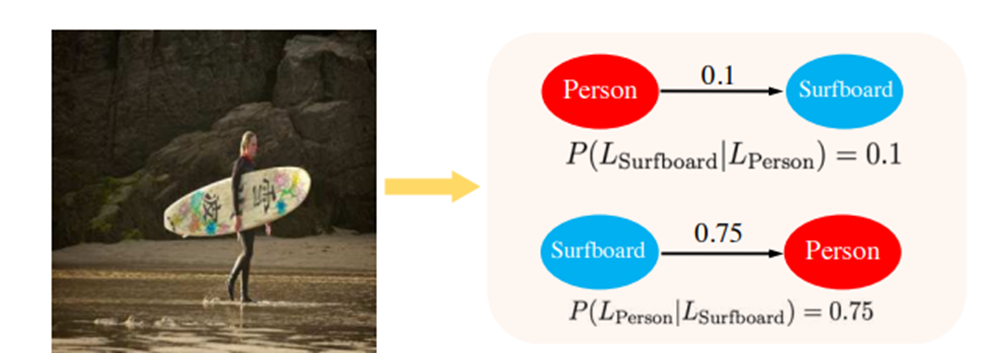
특히나 연결 유무를 따지는 0과 1로 구성된 adjacency matrix가 아닌, conditional probability로 구성된 matrix를 학습한다. 왜냐하면 위의 그림과 같이 "surfboard"가 있으면 사람이 높은 확률도 있지만, 사람이 있다고 "surfboard"가 있지는 않기 때문이다.

간단한 예시를 통해 Correlation matrix를 구해보자.

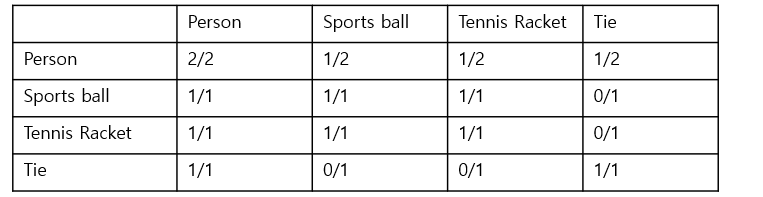
먼저 training dataset에서 함께 등장하는 label pair 갯수를 세어서 concurrence matrix $M$을 구한다. 그리고 각 label의 occurance time를 세어서 conditional probability matrix를 구할 수 있다. $P=M/N$

하지만 이러한 correlation matrix는 1) rare co-occurence가 noisy해지는 문제, 2) training dataset과 test dataset의 co-occurance 차이 문제가 발생할 수 있기 때문에, thresholding을 해준다. 여기서는 $\tau = 0.4 사용$

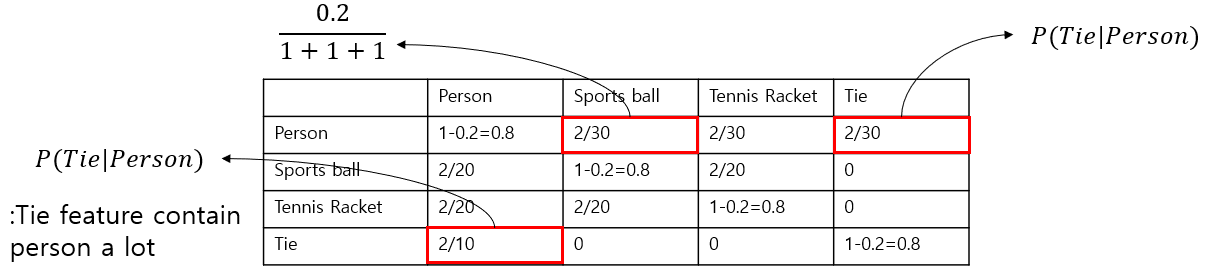
마지막으로 위의 GCN 개념에서 설명했듯이, 각 node의 feature는 adjacent node들의 feature의 weighted sum으로 표현되므로, over-smoothing problem이 발생할 수 있다. 즉, 비슷한 cluster (e.g., kitchen related vs. living room related)의 classifier vector가 매우 비슷해지는 경우가 발생할 수 있다. 이 를 해결하기 위해 이 논문에서는 re-weighting scheme을 사용하였다. (여기서는 p=0.2 사용)

Results

당시 MS-COCO/VOC2007 SOTA를 잠시 달성했던 것 같다.

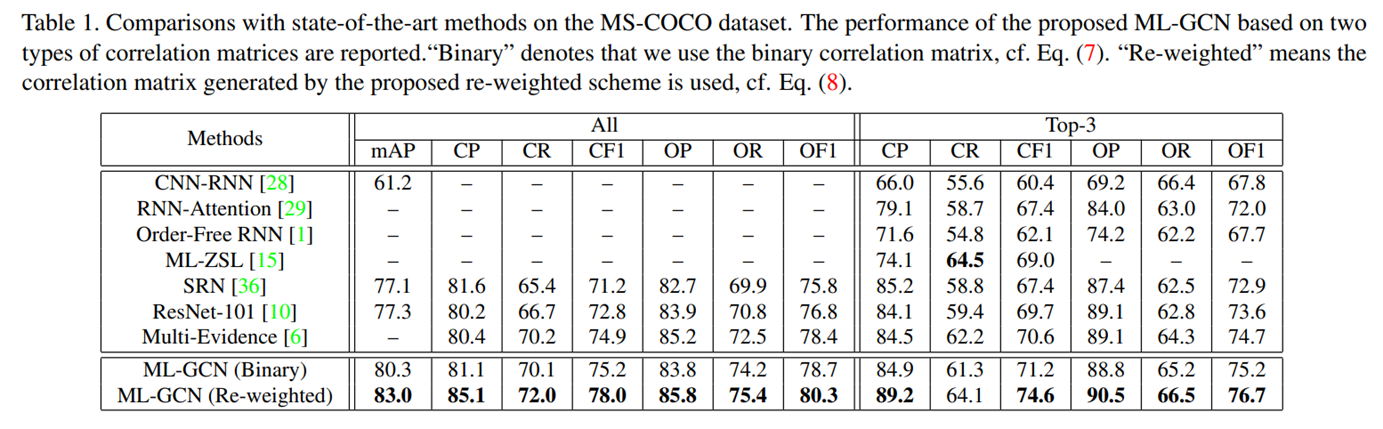
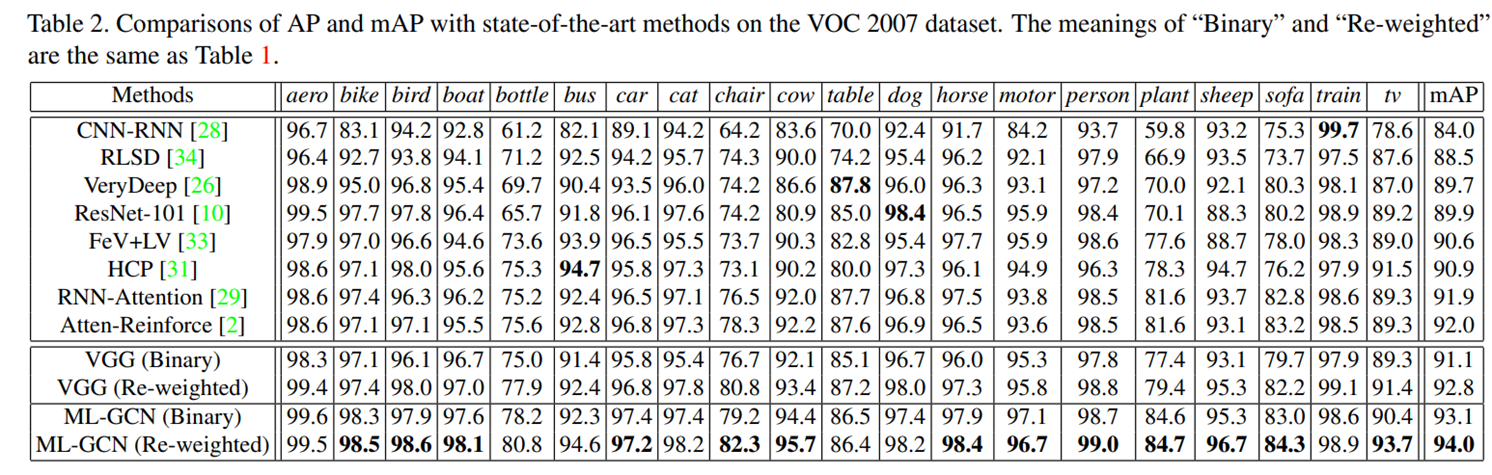
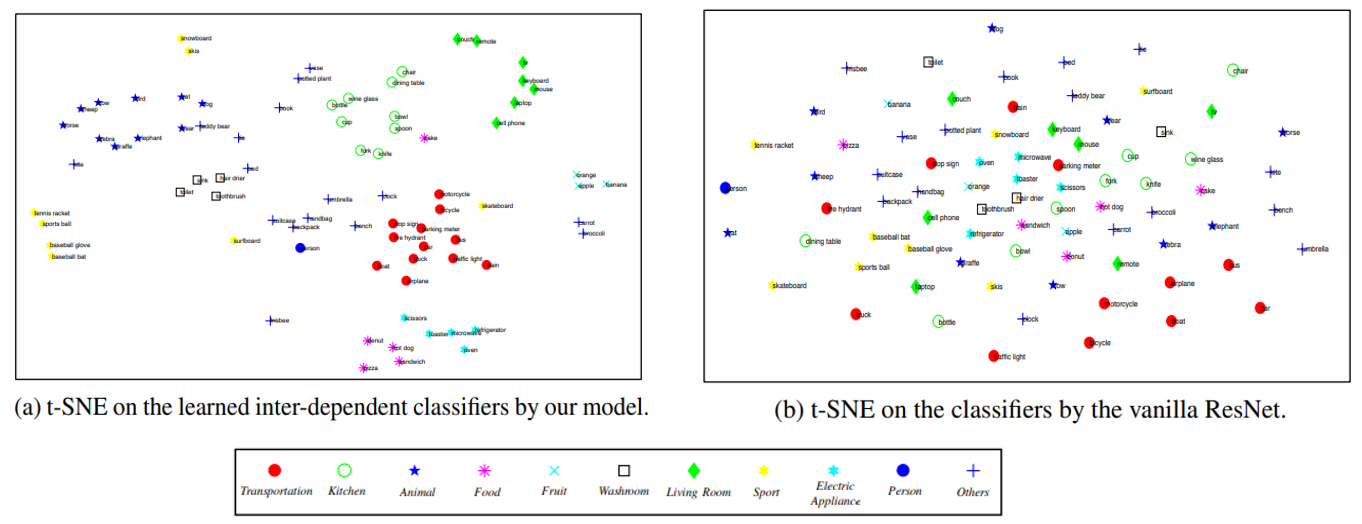
특히 baseline CNN의 classifier와 비교했을 때, GCN으로 학습된 classifier의 weight가 훨씬 더 잘 cluster를 이루고 있는 것을 확인할 수 있었다.

아래 그림은 Query 이미지와 kNN으로 가장 가까운 5개의 이미지와 해당 label을 추출한 것으로, ML-GCN 모델이 더욱 양질의 image representation도 학습할 수 있었다는 것을 보여준다.

Discussion

Data label의 dependency를 네트워크에 인코딩해줘서 image classification 성능을 높인 연구로, GCN이 효율적으로 잘 사용된 것 같다. 원래 classification을 할 때, 모든 label에 각각 classifier를 독립적으로 달아서 학습했었는데, 이러한 방식을 적용해보는 것도 재밌을 것 같다.

특히나 correlation matrix이 자체적으로 학습되는 구조이므로, 각 label 간의 상관관계가 어떻게 학습되는지 확인해보는 것도 흥미로운 주제이다.

하지만 논문에서도 언급되었듯이, 각 label vector가 학습될 때, 인접한 (혹은 관련 있는) feature vector가 합쳐지면서 smoothing 현상이 발생하므로, 이러한 architecture로 학습된 네트워크의 localization performance (e.g., CAM) 등의 성능은 조금 떨어지지 않을까 싶다.