Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks 리뷰

Paper : Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks (Jun-Yan Zhu, Taesung Park, Phillip Isola, Alexei A. Efros / ICCV 2017)

• Motivation : generative model 관련해서 처음 접한 논문이고, 큰 인상을 받았던 연구이다. CycleGAN으로부터 시작해서 후속 연구들을 꽤나 공부했고 실제로 이 논문 읽은 지는 오래되었지만, 간단하게 리뷰해보려한다.

Short Summary

1. Pair가 없는 두 도메인의 데이터에 대해 unsupervised image-to-image translation 방법을 제시한다.
2. Unsupervised image-to-image translation task 자체가 under-constrainted 문제이기 때문에, cycle-consistency loss를 소개하여 이 문제를 해결하였다.
3. Unsupervised I2I에서 당시 혁신적인 결과를 가지고 나왔다.

Introduction

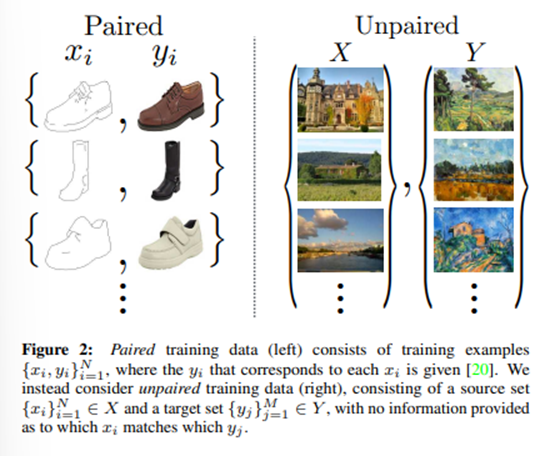
실제로 image to image translation task에서 paired dataset을 구하는 것은 매우 어렵다. 그렇기 때문에 해당 논문에서는 도메인 사이에 어떠한 underlying relationship이 존재한다는 가정 하에 unpaired image to image translation방법을 제안한다.

이론적으로는 pair 데이터가 없을 때에도, domain X와 domain Y의 이미지 세트가 주어졌을 때, $G : X \to Y$를 학습하여 $\hat y=G(x)$가 $y \in Y$와 구분하기 어렵도록 잘 학습하면, output distribution $\hat y$가 target distribution $y$와 matching 되도록하여 $X$ 도메인을 모두 $\hat Y$ 도메인으로 translate했을 때 $Y$도메인과 같아지도록 만들 수는 있을 것이다.

실제로는 이러한 translation은 x, y가 의미 있는 방향으로 pair를 형성했다고 장담할 수가 없다. 왜냐하면 $\hat y$와 같은 distribution을 갖는 G의 mapping이 수도 없이 많이 형성될 수 있기 때문이다. 또한 adversarial objective로 인해 mode collapse에 빠지는 경우도 많다.

이러한 문제를 해결하기 위해 해당 논문에서는 GAN의 object에 cycle consistent의 개념을 추가하였다. 즉, translator $G : X \to Y$ 와 또다른 translator $F: Y \to X$가 있다면 G와 F는 서로 역함수 관계여야하고, 양방향으로 mapping이 가능해야 한다는 것이다.

이를 구현하기 위해 G, F를 동시에 학습시키면서 $F(G(x)) \sim x$와 $G(F(y)) \sim y$가 되도록 학습하였다.

Formulation

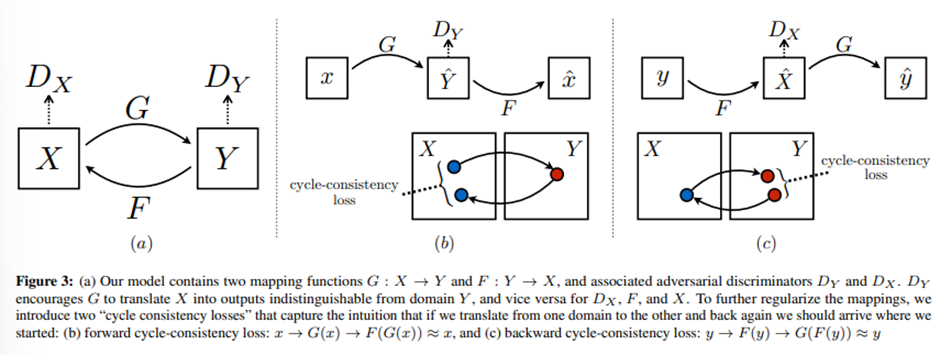
cycleGAN의 최종 목표는 도메인 X, Y사이의 mapping function $G : X \to Y$, $F : Y \to X$을 학습하는 것이다. 그리고 각각의 도메인에서 실제 이미지와 가짜 이미지를 구분하려는 Discriminator가 각각 존재한다.

Objective function은 생성된 이미지가 target 이미지의 distribution과 matching되도록 하는adversarial loss와 두 도메인 간의 mapping이 의미 있는 translation이 될 수 있도록 해주는 cycle-consistency loss로 이루어 진다.

adversarial loss

고전적인 GAN loss로, $G$는 $G(x)$가 도메인 $Y$의 이미지와 비슷해 보이도록 노력하고 $D$는 $G(x)$를 $y$와 구분하려고 노력한다.

이는 쌍을 이루는 양쪽 함수에 똑같이 적용된다. ($\mathcal L_{GAN}(F,D_X,X,Y)$)

cycle consistency loss

이론상 adversarial training은 mapping G나 F의 output distribution이 target domain의 distribution과 똑같도록 학습하는 것이 가능하나, 충분히 capacity가 큰 network는 같은 input 이미지를 target distribution과 똑같은 distribution을 가지면서도 수 많은 경우의 수로 mapping할 수 있기 때문에 의미 있는 mapping을 학습하기 위해 가능한 mapping 함수의 space를 줄여줄 필요가 있고 이를 위해 cycle-consistent가 필요하다.

위의 그림에 나와있는 것처럼 forward cycle consistency는 $x \to G(x) \to F(G(x)) \to x$, backward cycle consistency는 $y \to F(y) \to G(F(y)) \to y$를 학습한다.

두 mapping 함수는 동시에 학습되므로 cycle consistency loss는 다음과 같다.

Full objective

최종 목적 함수는 다음과 같다.

이 논문에서는 CycleGAN 모델을 두 개의 autoencoder를 학습하는 것으로 해석할 수도 있다고 한다.

이 autoencoder는 내부적으로 이미지를 intermediate representation으로 mapping하고 다른 도메인으로 translate하는 구조를 가지고 있다. (X를 Y로 mapping한 거 자체를 autoencoder에서 encoder가 latent code를 뽑은 거라고 생각하는 것 같음)

이는 autoencoder의 bottleneck layer가 target distribution을 따르게 하는 adversarial autoencoder의 특별한 케이스라고 볼 수도 있다.

우리의 케이스에서 $X \to X$의 target distribution은 도메인 $Y$이다.

Training Details

네트워크 구조 등은 생략하는 것으로 한다.

Training detail로는 negative log likelihood objective를 least squared loss로 바꿨을 때 학습이 더 안정적이라는 연구에 따라 LSGAN을 사용한다.

실제로 학습을 시킬 때에는 SSIM loss를 사용하는 것이 가장 좋은 quality의 output을 낸다.
또한 특정 데이터셋에 대해서는 아래의 identity loss를 추가하는 것이 도움이 된다.

이는 target domain의 sample이 input으로 들어왔을 때, input을 그대로 결과로 내놓게 regularize하는 term으로, input과 output의 color composition을 유지하고 싶을 때 사용한다.

Results

Cycle loss의 효과를 확인하였다.

다양한 image translation task에서 좋은 성능을 보였다.

Limitations

Training dataset에서 본적이 없는 데이터에 대해서는 잘 작동하지 않는 것을 확인할 수 있다.

Experiments

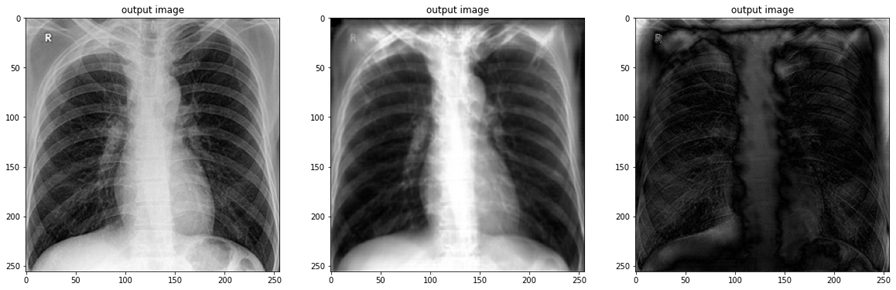
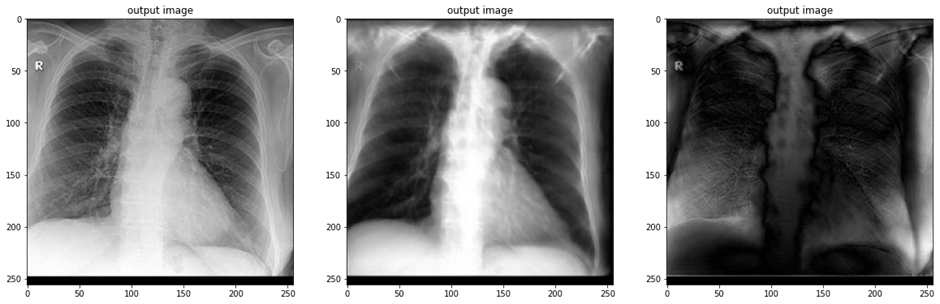
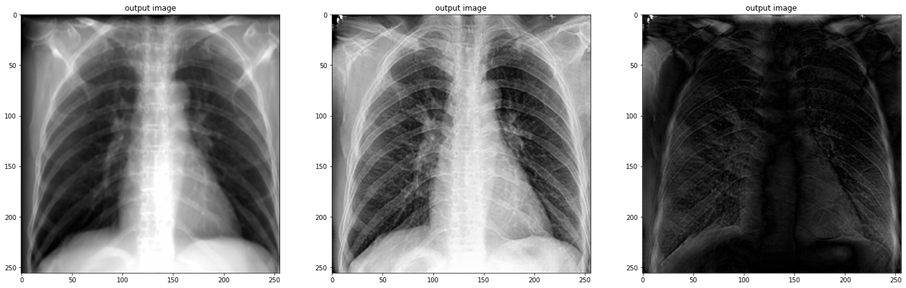
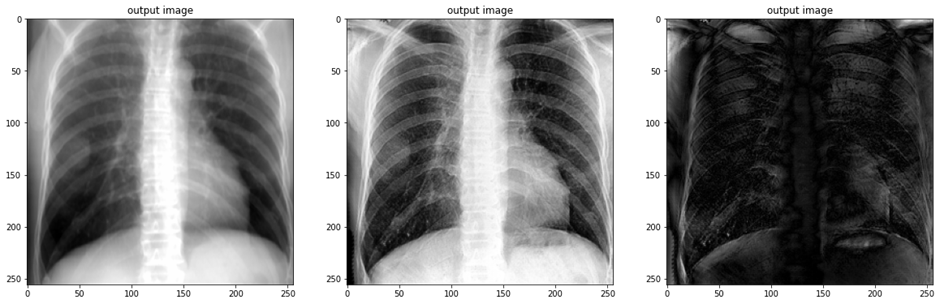
예전에 DRR projection한 이미지와 실제 X-ray image 사이에 cycleGAN학습을 진행한 결과이다. 나름 흥미로운 결과가 나왔는데, 도메인 간 차이가 좀 커서 몇몇 example에서 artifact가 발생되긴 했었다.

데이터 수도 충분하지 않았고. 개인적인 생각으로는 조금 더 발전시킨다면 X-ray 도메인 간 translation에 있어서는 괜찮을 거 같다.

Opinion

내용이 심플하고 재밌게 쓰여진 논문이다. 이 방법은 실제로도 여러 번 썼었고 잘 작동했다. 모델 자체도 가볍고 구현도 깔끔한 것 같다.

한 가지 단점이 있다면 deterministic mapping을 배우기 때문에, domain 간의 mapping이 확실하지 않거나 mapping할 경우의 수가 많다면 (예를 들어 X-ray normal $\to$ abnormal) 잘 학습하지 못한다. 그리고 512x512부터 high-resolution에서는 확연히 학습이 잘 안된다.