Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization 리뷰

Paper : Arbitrary style transfer in real-time with adaptive instance normalization (Huang, Xun, and Serge Belongie. / ICCV 2017)

• Motivation : Style Transfer 논문에서 매번 AdaIN을 이용하는 것을 보고 단지 Conv layer 사이에 norm layer를 활용해서 decoding 할 때, style을 바꿔주는 거라고 대략적으로만 이해하고 있다가 이 단순한 방법이 어떻게 style을 바꿔줄 수 있는지 궁금하여 읽게 되었다.

Short Summary

1. 이미지는 content와 style로 나뉠 수 있고, CNN을 통해 추출한 feature vector의 statistics는 어느 정도 이미지의 style를 표현하는 값이 된다.

2. Instance Normalization은 일종의 style normalization 역할을 수행할 수 있다.

3. Instance Normalization의 affine parameter를 학습하지 않고, 임의의 targe style image의 feature statistics를 활용해서 style normalization을 해주는 AdaIN을 사용하면 style transfer를 할 수 있다.

Introduction

image의 feature는 content와 style로 구분될 수 있으며, content를 유지한 상태에서 이미지의 스타일을 바꾸려는 연구가 지속적으로 진행되고 있다.

Gatys et al.은 처음으로 style transfer에서 neural algorithm을 제안하였다. 이때 convolution layer의 feature map의 statistics를 매칭시켜 원본 이미지의 content에 타겟 이미지의 style을 입혔다. (이후 대부분의 연구에서는 feature statistics transfer를 이용한 style transfer를 이용) 하지만 optimization 시간이 오래 걸린다는 단점이 있었다. 이를 극복하기 위해 feed-forward neural network를 학습하여 빠르게 style transfer를 하려는 시도가 있었지만, 한정적인 style 세트로만 transfer가 가능하다는 문제가 있었다.

이 논문에서는 두 가지 문제를 모두 해결하여 빠른 속도로 transfer가 가능한 동시에 arbitrary style을 적용할 수 있는 방법을 제안한다.

해당 논문에서는 Instance Normalization가 image의 style 정보를 담고 있는 feature statistics를 normalize함으로써 style normalize 기능을 수행할 수 있다는 새로운 해석을 시도했다. 이어서 단순히 content input의 feature statistics를 style input의 feature statistic로 normalize하는 AdaIN 방법을 제시하여 기존의 방법보다 빠른 feed-forward neural network로 다양한 인위적인 스타일로 변환을 시도하였다.

Background

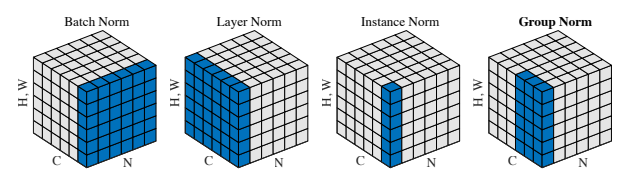출처 : Wu, Yuxin, and Kaiming He. "Group normalization." Proceedings of the European conference on computer vision (ECCV). 2018.

Batch Normalization

Batch normalization 기법은 feature statistics를 normalize하여 feed-forward network의 학습을 용이하게 하기 위해 사용된다.

여기서 $\gamma$와 $\beta$는 data로부터 학습되는 affine parameter이다. 그리고 batch normalization에서 평균과 분산은 각 feature channel마다 batch size와 spatial dimension을 대상으로 구해진다.

Batch normalization은 학습시에 mini-batch의 statistics를 사용하고 inference 시에는 가장 popular한 mini-batch의 statistics로 대체하기 때문에 두 phase간의 차이가 발생할 수 있다는 단점이 있다.

Instance Normalization

원래 original feed-forward style transfer 방법에서는 주로 batch normalization layer를 사용했다. 하지만 Ulyanov et al.은 Batch normalization layer를 Instance Normalization으로 바꾸는 것 만으로 큰 성능 향상을 얻을 수 있었다.

똑같이 affine transform parameter는 학습되는 parameter이지만, Batch normalization과 다르게, 여기서 평균과 분산은 각 channel 과 각 sample 별로 spatial dimension을 대상으로 구해진다.

또 다른 차이점은 instance normalization은 inference시에도 똑 같은 statistics로 normalization할 수 있다는 것이다.

Conditional Instance normalization

Instance normalization layer처럼 하나의 affine parameter를 배우는 대신에 각 style s마다 서로 다른 affine parameter를 학습하도록 하는 Conditional Instance Normalization도 있다.

학습 시에, 정해진 style set의 image들을 랜덤하게 선택해서 해당하는 style의 affine parameter를 학습시켰고, 놀랍게도 같은 parameter를 가지는 cnn에서 IN layer에서 다른 affine parameter를 쓰는것만으로 완벽하게 스타일이 다른 이미지를 만들어 낼 수 있다고 한다.

하지만 정해놓은 style 개수만큼 학습해야하는 parameter가 증가한다는 단점이 있다.

Interperting Instance Normalization

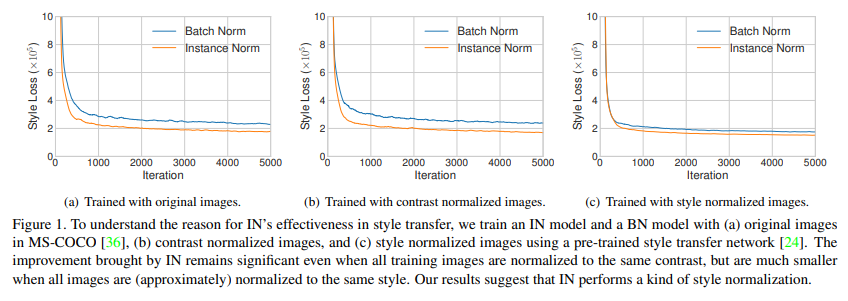
Instance normalization은 그럼 왜 style transfer에서 잘 되는 것일까? Batch normalization을 instance normalization으로 바꾸어 성능 향상을 확인한 Ulyanov et al.은 instance normalization이 image의 contrast에 invariance하도록 해주기 때문이라고 했지만, 이 논문에서는 Instance normalization은 feature space에서 하는 것이고, affine transformation parameter만 바뀌어도 style이 바뀐다는 사실을 생각하면 instance normalization이 더 많은 영향을 주고 있다고 생각했다.

이어서 instance normalization이 feature statistics인 평균과 분산을 normalize함으로써 style-normalization과 같은 역할을 수행하고 있다고 주장했다.

이 논문에서는 이를 확인하기 위해서 몇 가지 실험을 하였다.

첫번째 그래프를 통해 Single style transfer에서 Batch normalization을 IN으로 바꿔주는 것만으로 모델 convergence가 빨라지는 것을 확인할 수 있다. 두번째로 training image의 contrast를 normalize하고 학습했을 때도 IN의 model convergence가 빨랐다. 이 말은 IN의 효과가 단순히 image contrast에 invariance해서는 아니라고 할 수 있다. 마지막으로 pre-train된 style transfer network를 이용해 training image의 style을 normalize시킨 후 학습을 했을 때에는 IN의 효과가 확연히 떨어진 것을 확인할 수 있었다. 이 말은 말그대로 IN이 style normalization의 역할을 수행하고 있다는 것을 의미한다.

이러한 이해를 바탕으로 batch normalization을 생각하면, batch normalization은 mini-batch의 statistics를 사용하기 때문에, batch 내부 서로 다른 style이 하나의 style로 합쳐지고 이를 통해 normalization함으로써 제대로 style을 normalize할 수 없고, 이후 하나의 style로 transfer를 하더라도 여전히 다른 style을 가지고 있을 것이다.

반면에 IN은 각 이미지의 feature statistics를 사용하기 때문에 각각 이미지를 특정 target style로 transfer하는 것이 가능하다.

$\to$ 평균을 빼고 분산을 나누는 것을 해당 feature에서 style을 빼는 작업, affine transform parameter 람다를 곱하고 베타를 더하는 것을 feature에 style를 넣는 작업이라고 이해해도 좋을 것 같다.

Adaptive Instance Normalization

이 논문에서는 IN이 affine parameter로 정해지는 특정 style로 input을 normalize하는 역할을 수행할 수 있다면, 이 affine parameter를 임의로 부여하여 원하는 style로 transfer를 할 수 있다고 생각하였고, IN에서 간단한 modification을 통해 Adaptive Instance Normalization을 제안하였다.

AdaIN은 다른 normalization처럼 학습하는 parameter가 있는 것이 아니고, content 이미지와 style 이미지를 input으로 받아서 content 이미지의 feature statistics를 style 이미지의 feature statistics로 바꾸어 준다. 이때 affine parameter는 style 이미지로부터 바로바로 구해지는 것이다.

IN과 동일하게 statistics는 spatial dimension을 통해 각 channel과 각 sample별로 구해진다.

직관적으로 이해하기 위해 예를 들자면, 어떤 임의의 style을 추출하는 feature channel이 있다고 해보자. 그리고 내가 transfer하고 싶은 style 이미지가 그 style이라고 한다면, 아마 이 feature channel의 activation의 mean이 전체적으로 높을 것이다. AdaIN을 통해 이 mean을 content input image의 똑같은 channel feature에 옮겨준다면, content image의 spatial structure는 유지한 채로 average activation이 높아지게 될 것이다. (분산은 더 subtle한 정보를 전달해준다.) 그리고 이렇게 normalize된 feature가 decoder에서 image space로 옮겨지면 style이 바뀐 이미지가 나오는 것이다.

(+) 또는 이미지를 embedding한 양질의 feature map에서 강조할 feature를 재조정한다고 생각할 수도 있을거같다. 여전히 feature map에서 spatial한 정보는 유지가 된다.

정리하자면 AdaIN은 channel별 mean과 variance를 feature space에서 원하는 style의 것으로 바꿔줌으로서 style transfer를 수행하는 방법이다.

Architecture & Training

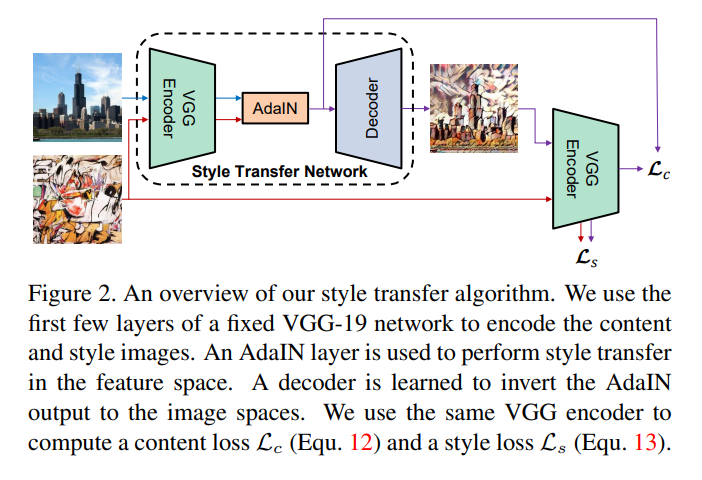
Style transfer network는 위의 그림과 같이 content 이미지와 임의의 style 이미지를 input으로 받고 둘이 합쳐진 결과를 내놓게 된다.
Pre-train된 VGG network를 fix시켜 feature를 둘 다 추출하고, adaIN layer를 통해 content 이미지의 평균과 분산을 style 이미지의 평균과 분산으로 normalize해준다.

Decoder는 style이 입혀진 feature $t$를 image space로 다시 돌이키도록 학습된다.

또한 decoder가 다양한 서로 다른 style의 이미지를 만들어낼 수 있도록 decoder의 layer 사이에는 IN과 BN을 사용하지 않았다. 그 이유는 IN과 BN이 각 이미지를 하나의 style로 normalize 해버리기 때문에 AdaIN을 통해 feature statictis를 바꾸어준 영향을 저해할 수 있기 때문이라고 생각한다.

Decoder를 학습하기 위한 loss는 content loss와 style loss로 구분된다.
Output 이미지를 다시 pre-trained VGG에 넣어 나오는 feature와 우리가 target하는 feature (AdaIN output)으로 나온 feature의 Euclidean distance를 content loss로 하고,

Encoder 내부에서 style 이미지와 output 이미지에 대해 각 layer마다 나오는 feature의 mean과 variance의 L2 loss를 모두 더하여 style loss로 사용하였다.

Result

기존의 방법들에 비해 inference speed와 style flexibility 관점에서 좋다. 또한 이미지 퀄리티가 훌륭하다.

additional

이 방법을 통해 style transfer를 할 때, color를 보존하면서 style transfer를 하거나, 서로 다른 spatial region에 대해 서로 다른 style을 적용할 수 있다고 한다.

먼저 color를 유지하면서 변화시키고 싶을 때는 input style 이미지를 input content 이미지와 같은 color distribution을 같게 하고, style transfer를 하면 된다고 한다. 말은 쉬운데, 정확하게는 어떻게 색상 분포를 같게 하는 지는 이해하지 못했다. 아무튼 변화시키고 싶지 않은 style은 처음부터 align 시킨 후 transfer를 하면 된다고 생각하면 된다.

위의 그림은 feature 상에서 masking을 통해 하나의 content의 다른 spatial region에 다른 style을 부여한 경우이다. 서로 다른 region에 따로 AdaIN을 적용하면 된다고 하는데, 아마 feature map에서 normalize하고(style 빼 주는 작업), spatial하게 masking한 뒤, 따로 affine transformation을 해주는 것 같다.

Opinion

Style Transfer에 관심을 가지면서 맨날 사용하는 방법에 대한 논문을 이제야 읽었다. 최근에 나오는 논문들은 decoder의 conv layer이후에 계속해서 AdaIN layer를 사용해서 generation complexity를 높이는 것 같다.

최근에는 X-ray image generation에 대해 계속 생각하고 있는데, Domain style transfer에서는 나름 잘 맞는 방법인 것 같은데, normal/abnormal style transfer에는 이게 잘 맞는 것인지 의문이 든다. 여기서 말하는 style은 조금 texture 정도에 가까운 느낌이었다. 고민이 필요하다.

그런데 마지막에 특정 style을 보존하거나, 서로 다른 style을 부여할 수도 있다는 부분은 매우 흥미로웠다. 단순히 드는 생각으로는… 폐 영역 내부에서만, 더 나아가면 특정 patch 내부에서만 style을 바꿔줄 수 있다면 원하는 장소에서 style을 변화시킬 수 있을까? 혹은 특정 패턴을 나타내는 feature map의 mean value를 emphasize하면 원하는 패턴을 집어넣을 수 있을까?