Neural Network의 high frequency 데이터에 대한 convergence에 대해

** 읽어보면 좋을 seminar works
1) Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains (Matthew Tancik, Pratul P. Srinivasan, Ben Mildenhall, Sara Fridovich-Keil, Nithin Raghavan, Utkarsh Singhal, Ravi Ramamoorthi, Jonathan T. Barron, Ren Ng / NIPS 2020)
2) Neural Tangent Kernel: Convergence and Generalization in Neural Networks (https://arxiv.org/abs/2006.10739) (Arthur Jacot, Franck Gabriel, Clément Hongler / NIPS 2018)
3) On the Spectral Bias of Neural Networks (Nasim Rahaman, Aristide Baratin, Devansh Arpit, Felix Draxler, Min Lin, Fred A. Hamprecht, Yoshua Bengio, Aaron Courville / ICMR 2019)
4) The Convergence Rate of Neural Networks for Learned Functions of Different Frequencies (Ronen Basri, David Jacobs, Yoni Kasten, Shira Kritchman / NIPS 2019)

• Motivation : Coordinate-based network에 관한 연구에서는 다양한 positional encoding이 제안되곤 하는데, 이때 당연시 여기는 것이 Neural Network는 high frequency detail을 학습하기 어렵다는 것이다. 위 논문에서 설명하는 방향에 맞춰 이해하려고 노력했다. method나 experimental result 등은 기술하지 않았다.

Introduction

위의 그림과 같이 low-dimensional coordinates를 input으로 받고, 그 input 위치에 대한 shape, density, color 등을 출력하도록 학습하는 network를 coordinate-based network라고 한다.

이런 coordinate-based network는 implicit neural representation (INR)으로도 생각할 수 있는데, 어떤 continuos signal을 neural network에 encoding한다는 의미에서 그렇다.

즉, 데이터를 저장하는 하나의 방법으로 생각할 수 있고, "implicit"이라는 단어에 집중해보면 아래와 같이 "explicit"과 구분해볼 수도 있겠다.

INR은 기존의 방식에 비해 여러 장점을 가지는데, 아래 정도로 정리할 수 있을 것 같다.
1) Continous representation & resolution agnostic
2) Memory Efficiency
3) Differentiable Rendering

아무튼 이것이 중요한 것은 아니고, 우리가 여기서 다룰 내용은 저 MLP에 들어가게 되는 coordinate input의 형태에 관한 것이다.

이미 여러 literature에서 neural network의 spectral bias에 대해서 다루고 , neural network가 low-dimensional input을 통한 학습에 취약하다는 것에 대해 다루었다.

이에 대해 많은 연구들은 잘 설계된 positional encoding을 통해 이러한 문제를 극복하고자 한다.

특히 이 논문에서는 Fourier feature를 사용한 input coordinate ($\bold v$)의 mapping을 통해 이러한 문제를 해결한다.

Kernel regression

ref: https://web.mit.edu/modernml/course/lectures/MLClassLecture3.pdf

Training dataset $(\bold X, \bold y)=\{(x_i, y_i)\}^n_{i=1}$가 있다고 하자.

$y_i=f(x_i)$인 scalar output으로, 우리는 임의의 point $x$에 대해 estimate $\hat{f}$를 구하려한다.

먼저 Linear regression에서부터 시작해보자.

$f(w,x)=w^Tx$라는 함수를 정의해서,

$L(w)=\frac{1}{2}\sum^n_{i=1}(y_i-f(w,x_i))^2$의 loss를 minimize하도록 하는 $w$를 구할 수 있을 것이다.

그런데, 여기서 linear model $f$는 representation에 한계가 있기 때문에, model에 nonlinearity를 추가하고 싶다.

이를 위해 어떤 nonlinear transform을 정의하고, 이를 $x$에 적용하여 어떤 feature map ($\phi$)을 만들고, 이를 통해 linear regression하는 방법을 생각할 수 있다.

예를 들어, 아래와 같은 non-linear transform을 통해 더 높은 차원의 feature space로 데이터를 옮기고 구분하기 쉽게 데이터를 represent하는 것이 가능해진다.

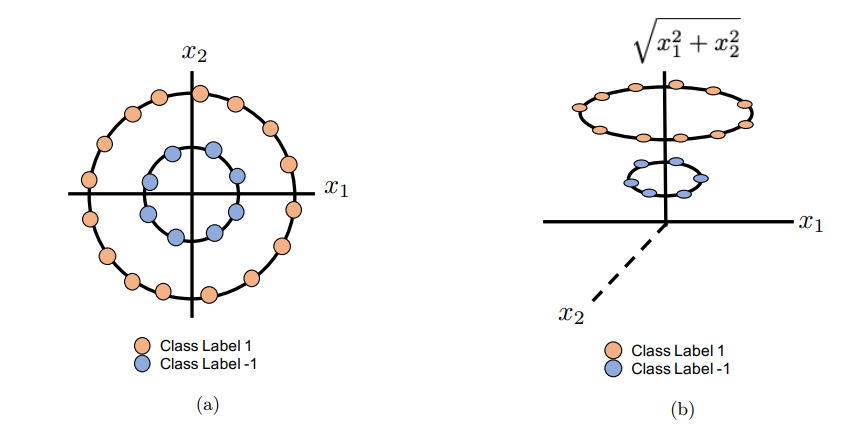
이때, Representer Theorem으로 인해, optimization problem의 solution이 training data point에서 evaluate된 kernel function의 선형 조합으로 구해질 수 있다. (여기서 증명하지는 않으려고 한다.)

그러면 우리는 linear regression문제를 풀기위한 loss function을 아래와 같이 다시 쓸 수 있는데,

여기서 중요한 점은 linear regression 문제를 풀기 위해서는 각 input feature의 내적 값만 있으면 된다는 것이다. 심지어 만약에 우리가 아래와 같이 두 feature의 내적값을 내어주는 어떤 function을 정의할 수 있다면, feature mapping $\phi$도 몰라도 된다.

이 함수가 바로 kernel function이고, 이러한 kernel을 이용한 linear regression을 kernel regression이라고 한다 (kernel trick).

Kernel regression을 생각하기 위해 다시 위에서 구한 loss function을 가지고 오면,

여기서 $\sum^n_{j=1}\alpha_j\phi(x_j)^T\phi(x_i)=\alpha K$라고도 쓸 수 있으므로, loss를 matrix form으로 쓰면

즉, 우리는 $y=\alpha \hat K$라는 n개의 variable이 있는 linear system을 푸는 것과 같고, particular solution을 아래와 같이 구해질 수 있을 것이다.

그러면 최종적으로 우리의 예측기는 아래와 같이 쓸 수 있다. (논문에 나온 식)

정리하자면, kernel regression은 training examples의 feature들의 superposition을 통하여 새로운 데이터에 대한 예측을 하는 것이라고 볼 수 있다.

(그림 출처: Every Model Learned by Gradient Descent Is Approximately a Kernel Machine (Pedro Domingos / arxiv)

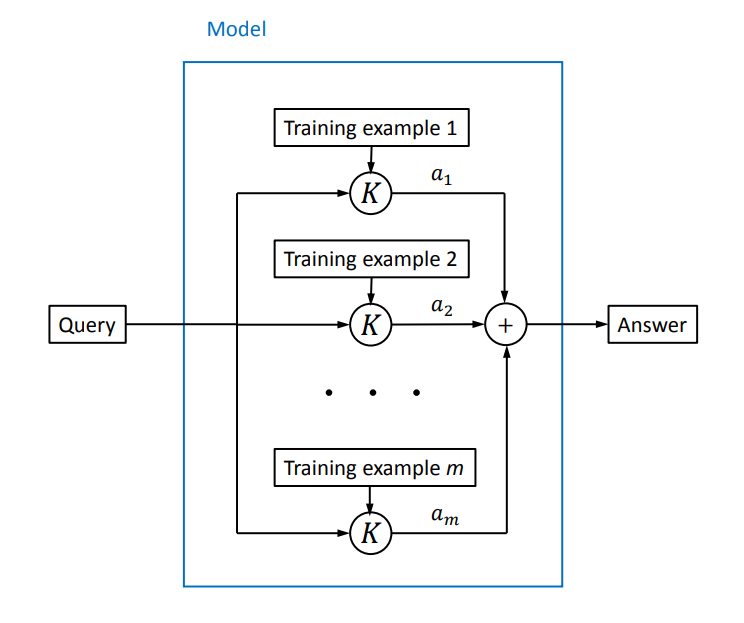
Neural Tangent Kernel (NTK)

Neural tangent kernel은 neural network training이 NTK를 사용한 kernel regression로 approximate할 수 있다라는 이론으로, deep wide neural network의 lazy training을 가정한다.

아래와 같은 1-layer MLP를 생각해보자.

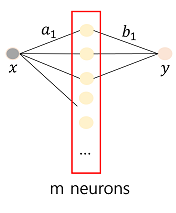
여기서 weight $a,b$를 학습하기 위해 위에서와 똑같이 regression loss를 사용할 수 있다.

Gradient descent based training을 하면

여기서 weight를 update한다는 것은 initial weight $\theta \sim \mathcal N$가 시간 $t$에 따라 학습된다는 것이다.

이때, neural network가 충분히 wide하다면 (i.e., $m>>1$), weight들이 거의 static하다고 하는데, 그러한 경우 weight $\theta$에 대해서 $\theta_0$에서 1st order taylor approximation를 생각해볼 수 있다.

즉, neural network model을 initialization point주변에서 linearization할 수 있게 있게 되는데, $\nabla_\theta f(x;\theta_0)$를 mapping function의 관점에서 본다면, 이를 kernel regression과 비슷하게 생각해볼 수 있다.

그러면 이에 해당하는 kernel function도 정의할 수 있게된다.

여기서, 추가적으로 gradient descent 분석을 하기 위해 $\eta \to 0$으로 보내 gradient flow dynamics를 구해보자.

여기서 $L(\theta)=\frac{1}{2}\sum(f(x_i;\theta)-y_i)^2$ 이므로

그리고, gradient trajectory를 따라 변하는 estimated output의 값을 추적해보면, (gradient flow dynamics 대입)

위와 같이 gradient-descent based neural network training을 NTK를 이용한 kernel regression으로 나타낼 수 있다.

Spectral Bias when training neural networks

Training error $e=\hat{y}-y=f(x;\theta)-y$를 정의해보자.

그러면

이제 time $t$에서 network의 output을 network 초기 output과 error를 통해 나타낼 수 있다.

논문 equation (3)에서는 초기 $f(x;\theta_0)$를 그냥 0으로 가정하고 아래와 같이 기술한 것 같다. (이상적인 training과정에서는 $K_{test}=K$이다.)($\eta$도 사실 그냥 상수 곱해준 것으로 크게 중요하진 않음)

이때, kernel matrix $k$는 positive semi definite하기 때문에 eigendecomposition ($k=Q \Lambda Q^T$)이 가능하고 $e^{-kt}=Qe^{-\Lambda t}Q^T$와 같이 쓸 수 있다. 그러면

위 식을 보면, error가 NTK의 eigenvalue 값에 따라서 decay되는 것을 알 수 있고, target function의 component 중에서 larger eigenvalue를 갖는 kernel eigenvector가 더 빠르게 학습한다는 것을 의미한다.

그런데 여기서 $k$의 eigenfunction ($columns\;of\;Q=q_i$)은 서로 orthogonal하기 때문에 fourier analysis에서 basis function의 역할을 할 수 있고, 이때 eigenvalue들은 각 eigenfunction의 amplitude, coefficient로 생각할 수 있다.

이러한 kernel들은 대부분 smoothing function인데, smoothing function의 경우 low frequency components가 energy가 집중되어있기 때문에 (거의 모든 정보가 low-frequency regime에 몰려있음), fourier coefficient가 더 크다. 즉, 더 큰 eigenvalue를 가진다. 반면에 high frequency components는 작은 eigenvalue.

작은 eigenvalue는 convergence가 잘 되지 않는다고 했으므로,

neural network는 high-frequency를 잘 학습하지 못한다는 것을 증명해 냈다.