Generative Adversarial Network

신희준·2023년 2월 9일

gan network

Background Knowledge

목록 보기

8/12

이번 글에서는 Generative Adversarial Network(GAN)의 basic concept에 대해서 이해해보자.

reference
1. Generative Adversarial Network (Ian J. Goodfellow)
2. From GAN to WGAN (Lilian Weng)

Supervised / Unsupervised Learning

Supervised learning(지도 학습)은 어떤 input x를 어떤 output y으로 mapping하는 함수를 학습하는 것으로, 상대적으로 straightforward한 목표를 가지고 있다.

머신 러닝에서 자주 접하는 task인 classification, regression, object detection, semantic segmenation 등이 모두 예시가 될 수 있다.

반면 unsupervised learning(비지도학습)은 어떤 정해진 목표가 있다기보다는 정답이 없는 input 데이터로부터 “의미있는 어떤 것”을 학습하는 것을 목표로 한다.

Clustering이나 Dimensionality reduction, Density estimation 등이 대표적인 예시가 될 수 있다.

이번에 다룰 주제는 Density estimation의 일종인 Generative modeling이다.

Generative Model

Generative modeling의 목표는 주어진 학습 데이터에 대해 같은 데이터 distribution에서 새로운 data sample을 만들어내는 데에 있다.

즉, $generative\;samples\sim p_{model}(x)$ 가 $training\;data\sim p_{data}(x)$ 와 비슷하도록 학습하는 것이 목적이다.

** 학습 데이터의 경우에도 딱 주어진 N개의 학습 데이터가 있다기보다는 학습 데이터를 생성해내는 어떤 확률 분포 생성기가 있다고 생각하는 것이 이해해 도움이 된다.

Density Estimation에는 크게 두 가지 종류가 있다.

Explicit Density Estimation
모델이 생성하는 데이터 분포 $p_{model}(x, \theta)$ 를 명시적으로 정의하고 문제를 푸는 경우를 의미한다.
예를 들어 확률 분포를 정규 분포로 가정하고, 주어진 데이터 $x$ 를 만들어낼 확률을 최대화 하는 parameter $\theta$ 의 확률 분포를 찾아내는 문제를 생각할 수 있겠다.
Implicit Density Estimation
모델이 생성하는 데이터 분포를 미리 정의하지 않고, $p_{model}(x)$ 로부터 데이터를 sampling할 수 있도록 하는 경우를 의미한다. 우리의 GAN은 여기에 속한다.

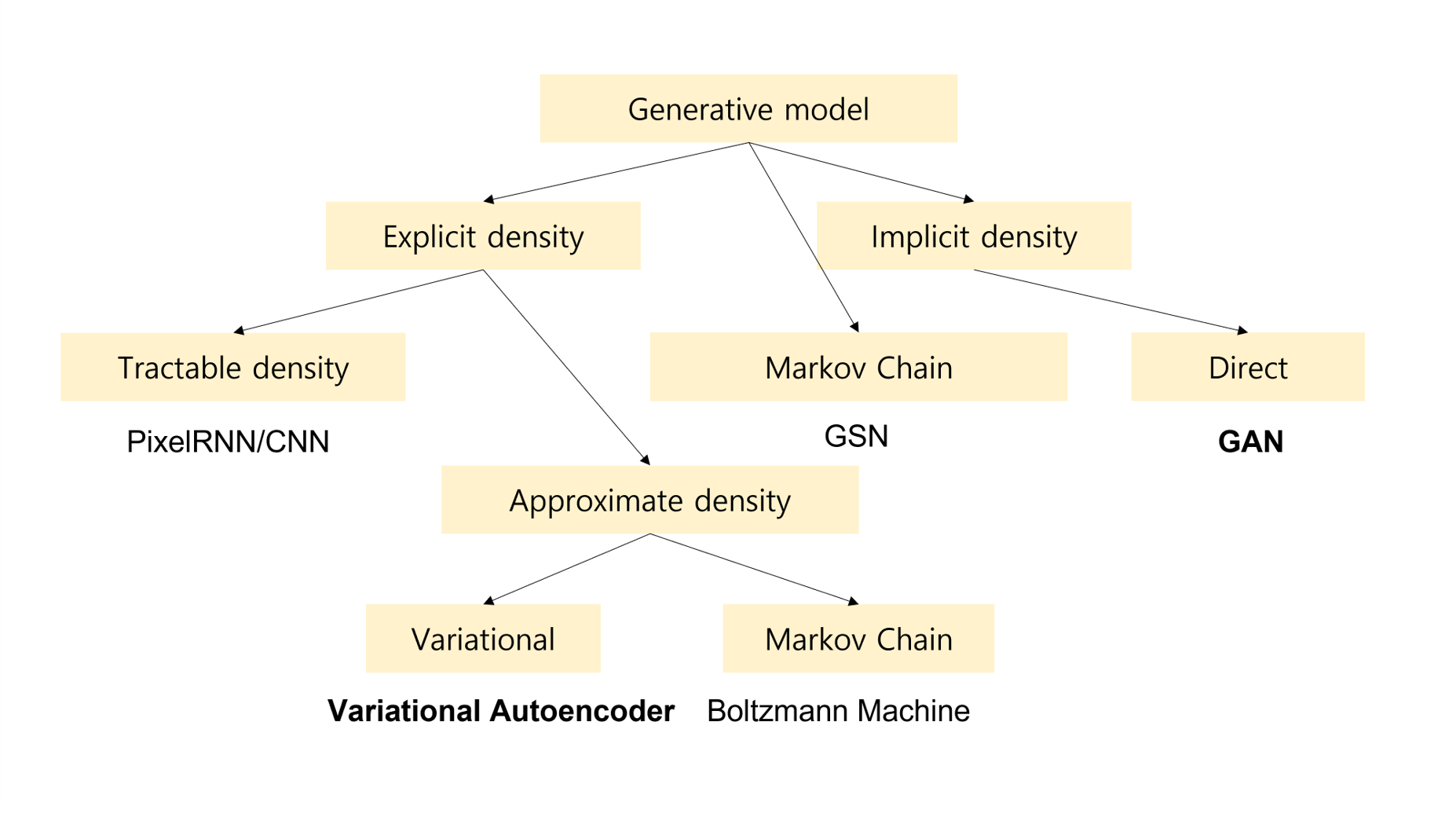
GAN

GAN은 generative model의 한 종류이다. 궁극적인 목표는 실제 데이터 셋에 있을 법한 이미지를 잘 생성해내는 것이다.

세상의 어떤 것으로도 변할 수 있는 것들이 모여 있는 공간을 latent space라고 한다. 이 latent space에 있는 임의의 벡터는 어떠한 machine이나 function을 통해 의미있는 무언가로 변하게 된다.

어떤 엄청난 생성 기계(perfect machine)는 정확하게 이 latent space의 vector를 가지고 우리가 가지고 있는 실제 데이터 셋 내부의 이미지로 정확하게 변화시킬 수 있다고 하자.

그럼 이제 우리가 하고자 하는 것은 generator가 이 생성 기계를 따라할 수 있도록 학습하는 것이다.

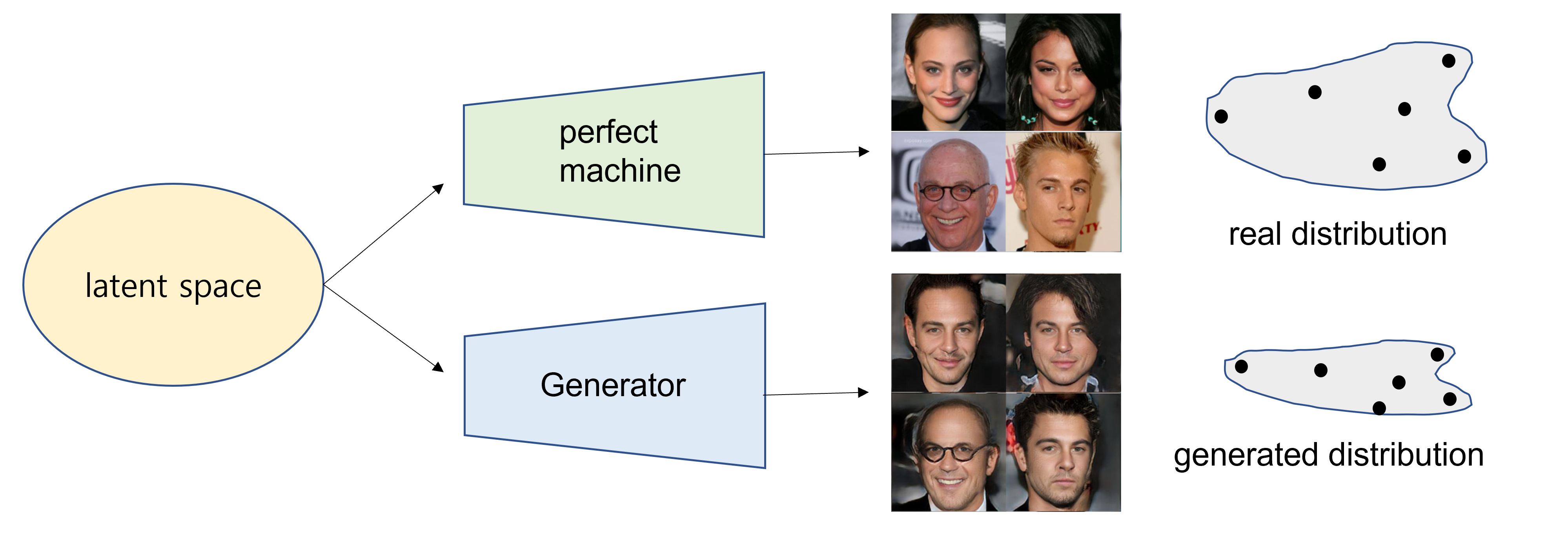
** 위 예시는 실제로 stargan 학습해본 결과

Latent Vector Sampling

문제는 perfect machine이 어떻게 latent vector를 원하는 데이터로 변환시키는지 우리는 알 수 없기 때문에, 여러 번 sampling해서 실제 분포가 어떠한지 추론해서 generator를 학습시켜야 한다.

실제로는 이 latent space조차도 어떻게 생겼는지 알 수가 없으므로 보통은 normal distribution에서 sampling을 하게 된다.

즉, 초기의 latent space는 아무런 의미도 갖지 않는 공간이다.

이 random vector를 generator에게 주고, 어떠한 이미지를 생성하도록 학습한다. 계속해서 학습을 진행하다 보면, generator가 이 latent vector를 특정 이미지에 연관 짓기 시작한다.

처음에는 완전히 다른 분포의 이미지를 만들어내겠지만, 점차 학습이 진행되면서 최대한 원하는 데이터 분포에 가깝게 만들어내게 되고, latent vector가 변함에 따라 의미 있는 이미지를 만들어낼 수 있다.

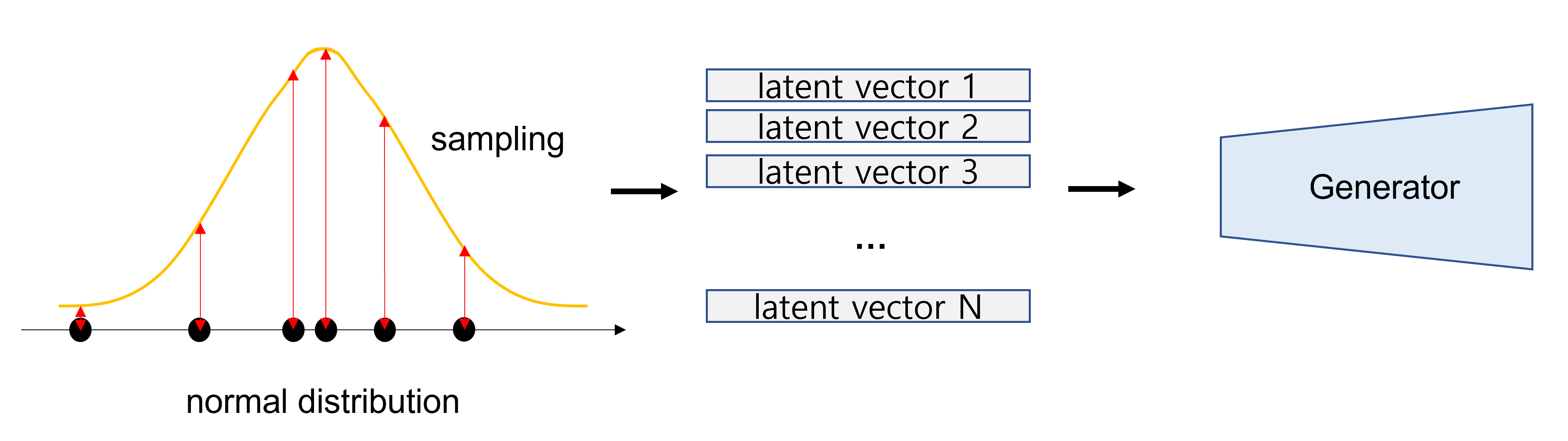
그러면 generator를 어떻게 학습시킬까?

GAN Framework

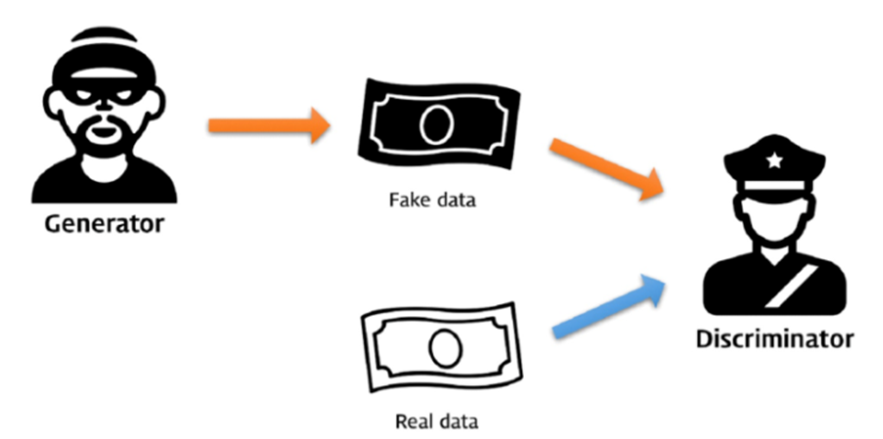
GAN은 보통 neural network를 이용한 두 개의 모델 사이의 Game Theory에 기반한다.

Generator는 계속해서 가짜 데이터를 만들어내고, Discriminator는 가짜 데이터와 진짜 데이터를 구별하려고 한다. 위의 그림과 같이 위조 지폐범과 경찰 사이의 경쟁이라고 생각하면 쉽다.

Discriminator는 진짜와 가짜를 구별하려고 하고, Generator는 discriminator가 진짜와 가짜를 구별하지 못하도록 만들어야 하므로, 말그대로 adversarial한 학습 방식이다.

두 모델은 함께 성장하지만, 결국에 우리는 Generative model을 만들려고 하므로, generator가 아주 완벽한 가짜 데이터를 만들어내고 discriminator는 진짜와 가짜를 구별할 수 없게 되는 것이 목표이다.

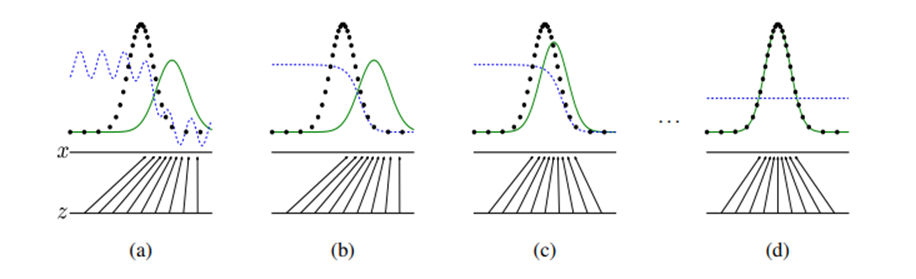
위의 그림은 학습 과정을 간단히 도식화 한 것이다. 쉬운 이해를 위해 1-D gaussian distribution에서 데이터가 생성된다고 생각하자.

초록색 선은 generative distriubtion ( $p_{model}$ ), 파란색 선은 discriminator function, 검정색 선은 data generating distribution ( $p_{data}$ ) (Generating distribution이라고 표현한 이유는 우리는 이미 실제 데이터가 있지만 그 조차도 어떠한 분포를 통해 샘플링 된 것이라고 생각하는 게 더 합리적이기 때문)

(a)는 아주 초기 initializ된 네트워크를 나타낸다.

(b) Discriminator 먼저 학습을 시킨다고 해보자. 그러면 discriminator는 data generating distribution에서 추출된 데이터와 generative distribution에서 추출된 데이터를 분류하려고 할 것이다. 이때 discriminator의 함수는 아래의 방향으로 최적화 될 것이다.

D^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{model}(x)}

(d) 최종적으로 nash equilibrium에 도달하면 $p_{model} = p_{data}$ 가 되기 때문에 두 모델은 더 이상 발전할 수 없다. 그리고 D는 이 둘을 구분할 수 없기 때문에 $D(x) = 0.5$ 가 될 것이다.

$\to$ GAN 학습 방법에서 최종 지향점은 $p_{model} = p_{data}$ 가 되는 equilibrium에 도달하는 것이다.

Little Mathmatics

Basic Formula

GAN 학습을 위한 loss function을 한번 살펴보도록 하자.

간단한 수식으로 나타내기 위해 다음과 같이 정의하면

$p_z$ : Data distribution over noise input $z$
$p_g$ : The generator's distribution over data $z$ = $p_{model}$
$p_r$ : Data distribution over real sample $x$ = $p_{real}$

Discriminator와 Generator의 minimax game에 대한 loss function을 아래와 같이 정의할 수 있다. (하나의 함수에 대해 Discriminator는 최대화하도록, Generator는 최소화하도록 최적화한다.)

\underset{G}{min}\underset{D}{max}\;L(D,G) = \mathbb E_{x\sim p_r(x)}[logD(x)] + \mathbb E_{x\sim p_z(x)}[log(1-D(G(z))] \\= \mathbb E_{x\sim p_r(x)}[logD(x)] + \mathbb E_{x\sim p_g(x)}[log(1-D(x))]

Discriminator는 real data에 대해 최대 probability를 내려고 하고, fake data에 대해 0에 가까운 probability를 내려고 한다. 반면 Generator는 Discriminator가 fake data에 대해 높은 probability를 낼 수 있도록 더 양질의 데이터를 만들어내려고 노력한다.

Optimal Value

위에서 정의한 loss를 이용해 학습하면 optimal한 상황에서 Discriminator가 내놓는 값은 어떠할까?

Discriminator 입장에서는 데이터 셋 내부 모든 데이터 x에 대한 아래 식을 최대화 해야 한다.

L(G,D) = \int_x{(p_r(x)log(D(x)) +p_g(x)log(1-D(x)))dx}

식을 단순화하고 적분식 안에만 생각하면 다음과 같이 간단히 적을 수 있다.

\tilde x=D(x),\;A=p_r(x),\;B=p_g(x)

f(\tilde x)=Alog(\tilde x)+Blog(1-\tilde x)

\frac{df(\tilde x)}{d\tilde x}=A\frac{1}{ln10}\frac{1}{\tilde x}-B\frac{1}{ln10}\frac{1}{1- \tilde x} =\frac{1}{ln10}(\frac{A}{\tilde x}-\frac{B}{1 - \tilde x}) = \frac{1}{ln10}\frac{A-(A+B)\tilde x}{\tilde x(1- \tilde x)}

미분 값이 0일 때, 최대 값을 가질 것이므로, 아래의 최적값을 가지게 된다.

D^*(x) = \tilde x^*=\frac{A}{A+B}=\frac{p_r(x)}{p_r(x)+p_g(x)}

만약 Generator가 optimal하게 학습이 된 경우 $p_g=p_{model}$ 가 $p_r=p_{data}$ 가 매우 가까워질 것이므로 $p_g =p_r$ 일때 discriminator는 0.5의 probability를 출력으로 내놓게 된다.

이 경우 최종 loss는 아래의 값을 가지게 될 것이다.

L(G,D^*) = \int_x{(p_r(x)log(D^*(x)) +p_g(x)log(1-D^*(x)))dx} \\=log\frac{1}{2}\int_x{p_r(x)dx} + log\frac{1}{2}\int_x{p_g(x)dx} \\=-2log2

Meaning of Loss function

사실 GAN에서 사용되는 위의 loss function은 쉽게 생각하면, discriminator가 optimal할 때, real data의 distribution $p_r$ 과 generative distribution $p_g$ 사이의 similarity를 구하는 것과 다름이 없다.

두 분포의 similarity는 JS divergence를 통해서 구할 수 있다.

D_{JS(p_r||p_g)} = \frac{1}{2}D_{KL}(p_r||\frac{p_r +p_g}{2}) + \frac{1}{2}D_{KL}(p_g||\frac{p_r +p_g}{2})

=\frac{1}{2}(log2+\int_x{p_r(x)log\frac{p_r(x)}{p_r(x)+p_g(x)}dx} + \frac{1}{2}(log2+\int_x{p_g(x)log\frac{p_r(x)}{p_r(x)+p_g(x)}dx}

=\frac{1}{2}(log2+L(G,D^*))

\to L(G,D^*)=2D_{JS}(p_r||p_g)-2log2

마찬가지로 optimal한 상황에서 generator는 완벽하게 real data distribution을 복제해내고, JS값이 0이 되므로 loss function은 $-2log2$ 가 된다.

[+] KL divergence & JS divergence

참고용으로 대강 어떠한 개념인지만 짚고가자.

(1) KL(Kullback-Leibler) Divergence
두 확률 분포의 차이를 계산하는 데 사용하는 함수로, $p$ 라는 확률 분포가 또 다른 확률분포 $q$ 에 얼마나 다른지를 계산한다.

KL(p||q)=\int_xp(x)log\frac{p(x)}{q(x)}dx

KL divergence는 $p(x)=q(x)$ 인 경우 0의 최솟값을 갖는다.

첨언하자면 KL divergence는 우리가 자주 사용하는 Cross Entropy에서도 유도될 수 있다.

H(p, q) = -\sum_i p_ilogq_i

= -\sum_i p_ilogq_i-\sum_i p_ilogp_i +\sum_i p_ilogp_i

= H(p) + \sum_i p_ilogp_i -\sum_i p_ilogq_i

= H(p) + \underset{KL \; divergence}{\underline{\sum_i p_ilog\frac{p_i}{q_i}}}

즉, cross entropy는 확률 분포 $p$ 의 엔트로피 $H(p)$ 에 두 분포 $p$ 와 $q$ 의 정보량 차이 항이 더해진 형태라고 볼 수 있고, 대게 $H(p)$ 는 상수이므로, cross entropy를 minimize한다는 것은 KL을 minimize하는 것으로도 생각할 수 있다.

하지만 KL divergence 함수는 asymmetric한 함수이다. ( $KL(p||q)$ 와 $KL(q||p)$ 는 다른 값을 가진다.) $\to$ KL divergence가 거리의 개념이 아니라는 말을 하곤 한다.

이러한 성질은 $p(x)\sim0$ 인 경우 $q(x)$ 의 영향이 무시되도록 하므로, 두 분포를 동등하게 비교하기에는 부적합할 수도 있다.

(2) Jensen Shannon divergence
두 확률 분포의 차이를 거리의 개념으로 구할 수 있는 함수이다.

JS divergence는 두 분포에 대한 KL divergence를 구하고 평균을 내는 방식이다. 이 함수는 symmetric한 함수이며 KL보다 smooth하다.

D_{JS}(p||q)=\frac{1}{2}D_{KL}(p||\frac{p+q}{2})+\frac{1}{2}D_{KL}(q||\frac{p+q}{2})

Problems of GAN

하지만 GAN도 분명히 단점이 존재한다. 사실 GAN은 density function을 직접 조금씩 fitting하는 것이 아니고, generator network의 parameter를 학습시키는 것에 불과하므로 optimal parameter로 학습하기가 어렵다.

Hard to achieve nash equilibrium

일단 알고리즘의 특성상 converge하기가 매우 어렵다.

GAN에서 discriminator와 generator는 nash equilibrium을 찾기 위해 동시에 학습되지만, 각 모델은 cost function에 대해 독립적으로 update 되고, non-cooperative한 상황에서 gradient update가 수렴할 것이라고 보장하기가 힘들다.

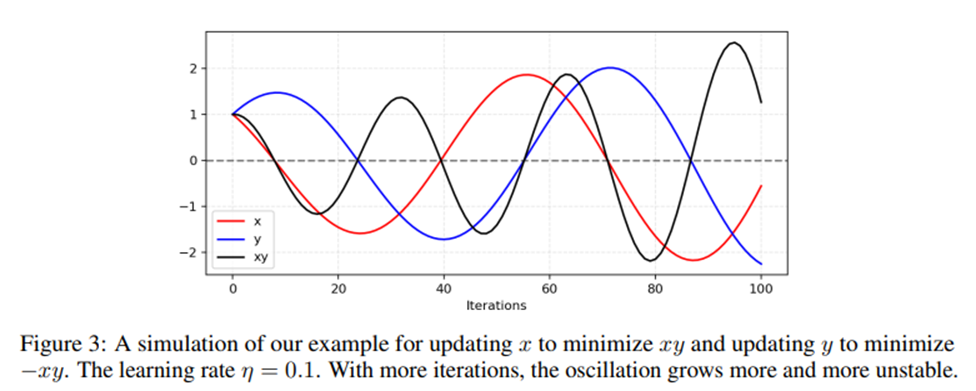
Adversarial한 학습에 대한 쉬운 예시로, 두 개의 모델을 학습하는데, 하나의 모델은 $f_1(x) = xy$ 를 최소화하기 위해 $x$ 를 control하고, 동시에 다른 모델은 $f_2(y) = -xy$ 를 최소화하기 위해 $y$ 를 control한다고 해보자.

이때, $\frac{\partial (𝑓_1)}{\partial 𝑥} = 𝑦$ , $\frac{\partial (𝑓_2)}{\partial y}= -x$ 이기 때문에 $x$ 를 업데이트 할 때 $𝑥−\eta 𝑦$ 를, $y$ 를 업데이트할 때 $y+\eta 𝑥$ 를 사용해야 한다.

그러므로 $x$ 와 $y$ 가 한번 서로 다른 부호를 갖게 되면, 아래의 그림과 같이 gradient update는 큰 진동을 유발하고 학습이 불안정하게 될 것이다.

Low dimensional Supports

우리가 $p_r$ 이라고 표현하는 실제 데이터는 사실 매우 높은 차원의 데이터이다. 예를 들어 12x12 크기의 이미지를 표현하기 위해서는 144차원이 필요하며, 각 픽셀이 가질 수 있는 value(0~255)에 따라 표현할 수 있는 이미지의 수가 $256^{144}$ 개나 될 것이다.

이러한 고차원을 머릿 속으로 그릴 순 없지만, 실제로 이런 고차원에서 데이터는 매우 낮은 밀도로 분포되어 있다. 즉, 의미있는 이미지는 어딘가에 몰려있을 것이고, 나머지는 대부분 noise 이미지일 것이다.

Manifold Learning의 기본적인 가정은 고차원에서 낮은 밀도로 형성되어있는 데이터의 집합을 포함하는 저차원의 manifold가 존재한다는 것이다.

잘 모델링한 manifold를 통해 데이터를 압축하여 표현할 수 있고 이러한 manifold의 확률 분포를 추측하여 데이터를 생성하고자 하는 것이 GAN이었다.

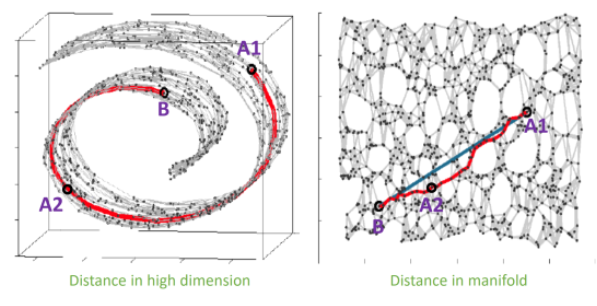그림 출처 : https://www.slideshare.net/NaverEngineering/ss-96581209

하지만 문제는 이렇게 low dimension manifold에 위치하는 $p_r$ 과 $p_g$ 함수가 실제로 high dimension의 데이터를 잘 표현해내는 것이 어렵다는 것이다.

High dimensional space안에서 low dimensional manifold에는 disjoint가 발생할 확률이 높다.

아래 그림은 3차원의 공간에서 두 직선과 두 평면이 가질 수 있는 overlap을 보여준다. 저차원으로 projection된 경우 아무리 두 manifold가 잘 overlap된다고 하더라도, 실제 high dimension에서는 어쩔 수 없이 disjoint가 발생할 것이다.

헷갈리지 말 것 : 우리는 실제로 이 저차원의 manifold 내부에서 함수를 정의한다. generator function은 이 manifold 내부의 어떤 latent vector를 mapping, real data generating function은 사실은 아주 고차원의 데이터를 input으로 받는 고차원의 함수인데, 이것을 manifold 가정을 통해 저차원으로 생각하는 것이고, 이 때문에 어쩔수없이 non-overlapping disjoint가 발생한다는 것이다.

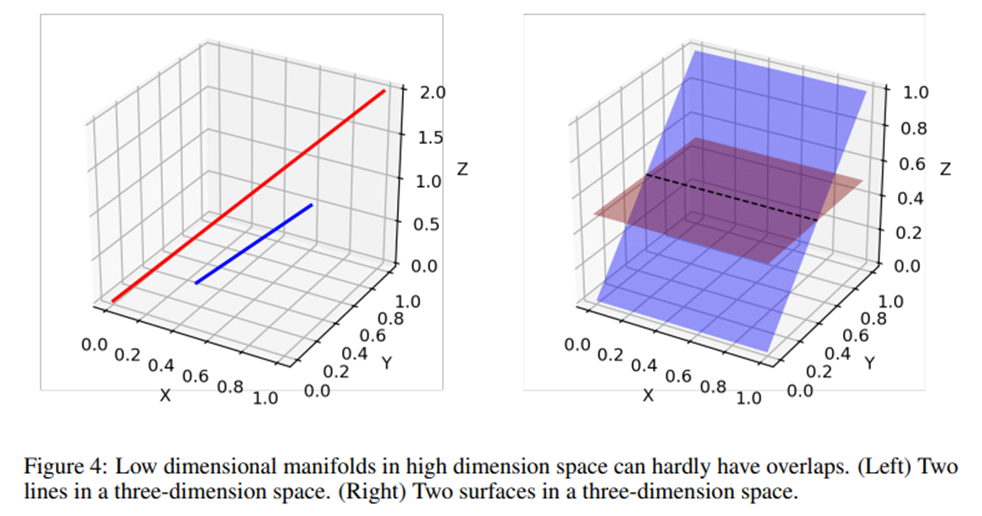
이러한 disjoint space가 있으면 분명히 어떠한 경우에는 완벽한 discriminator가 생겨나기 마련이다.

Vanishing gradient

Discriminator가 완벽한 경우엔, real data에 대해 1의 출력을 내고, fake data에 대해 0의 출력을 낼 것이다. 이러한 경우, 우리가 정의한 loss function은 0의 값을 가질 것이다. 즉, gradient또한 0이고, 학습이 진행되지 않을 것이다.

GAN은 framework 자체가 약간의 dilemma를 가지고 있다.

Discriminator가 너무 못하면, generator가 적절한 피드백을 받지 못함
Discriminator가 너무 잘하면, loss의 gradient가 0에 수렴하여 학습이 잘 되지 않는다.

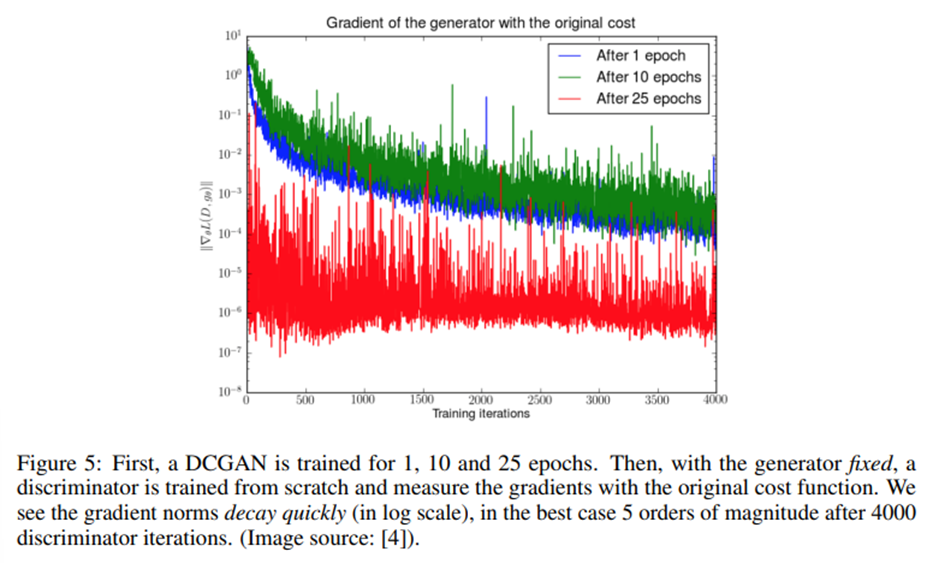
위 그래프는 파란색/초록색/빨간색 순으로 generator가 충분히 학습된 상태에서 discriminator를 from scratch로 학습시킨 것. 파란색의 경우 generator가 잘 학습이 안된 상태에서 discriminator는 진짜와 가짜를 완벽하게 구분하기 쉬울 것이므로, gradient가 급격하게 감쇠하는 것을 확인할 수 있다.

Mode Collapse

최신의 GAN에서도 자주 발생하는 흔한 문제로, generator가 학습 시, 매번 똑같은 output만을 생성하는 경우를 말한다.

Generator가 실제 데이터의 분포를 반영하지 못하고, variety가 적은 아주 작은 space에 갇혀버린 경우이며, discriminator를 속일 수 있는, 아주 일부분의 데이터만을 만들어낸다.

Loss 입장에서 쉽게 local minima를 찾을 수 있는 방법이므로 GAN 학습시 이러한 문제가 발생하는 경우가 많다.

Comment

GAN의 기본적인 개념에 대해 공부해보고 이 학습법의 inherent problem에 대해서도 간단히 살펴보았다.

여기서 다룬 내용은 아주 기초적인 내용으로, 이를 이해하기 위해 커버해야하는 방대한 연구 내용이 있으며, GAN은 아주 빠른 속도로 발전하였다.

GAN은 제약이 적고, high-resolution image를 포함하여 복잡한 데이터 분포에 대해 현실적인 이미지를 만들어낼 수 있다는 매력을 가지고 있다.

위에서 언급한 문제점들은 하나하나 해결해나가며 아주 정교하고 멋진 architecture 및 framework를 제공한 연구들도 매우 많다. 이러한 기술의 발전을 보고 배우고, 체험해보는 것은 나에게 너무나도 재밌는 일이다.

GAN뿐 만이 아니라 diffusion model을 이용한 generative task도 엄청나다는 연구가 있다. 이런 것도 나중에 꼭 공부해보고 싶다.

나는 개인적으로는 AI를 생각할 때, 사람만큼 하는 것보다도 사람보다 잘할 수 있는게 무엇이냐라는 생각을 한다. 이러한 관점에서 나는 Discriminative task보다도 Generative task가 AI가 잘할 수 있는 분야인 것 같다. (물론 generative task를 잘 수행하려면 discriminative feature를 잘 학습해야겠지만...)

예를 들어 아르마딜로랑 천산갑을 구분한다고 해보자. 사람은 각각 두장만 보고도 사실 이를 구분할 수 있지만, AI로 하여금 이런 일을 하게 하려면 엄청나게 많은 데이터가 필요할 것이다.

근데 이러한 이미지를 그린다고 생각해보자. 나는 10만장을 줘도 못한다.

비유가 조금 이상하긴 한데, 아무튼 똑같이 데이터를 feeding 한다는 관점에서 봤을 때, 무언가를 구별하는 것보다는 어떤 새로운 것을 만들어낸다는 것이 조금 더 의미있어 보였다.

요즘에는 ChatGPT와 같은 NLP generation model이 엄청난 이목을 받고 있다. 또한 내가 글을 쓰는대로 실시간으로 이미지를 만들어주는 generative model도 생겨나고 있다.

여유가 생길 때 마다 조금씩 조금씩 공부해보고 싶다.

엄청난 기술 발전의 시대에 살고있는 것 같다. 다채로운 연구들을 맛보고 소화시킬 수 있는 것만으로도 나한테는 행운이다.

신희준

공부하고 싶은 사람

이전 포스트

Classification Performance Metric

다음 포스트