Topological Image modification for object detection and topological image processing of skin lesions

• Author: Robin Vandaele, Guillaume Adrien Nervo, Olivier Gevaert

• Read: 2022년 5월 9일

• Subject: Topological Data Analysis, Computer Vision, Image Processing, Object Detection

• Submit: 2020년 12월 3일

• URL: https://www.nature.com/articles/s41598-020-77933-y

Summary

• ISSUE : 이미지에서 무관한 정보를 버리고 적절한 영역 내의 중요한 오브젝트를 식별하게 하고 싶다.
• SOLUTION : 이미지 데이터의 Persistent homology에서 적절한 threshold를 선택하는 것으로 무관한 object를 파괴한 뒤, topological property에 따라 해당 영역을 매꿈.

Main Idea

이 논문의 핵심 아이디어는 topologically significant하지만 irrelevant한 object를 제거하는 것이다.
이 아이디어는 중요한 object는 적어도 이미지의 테두리에 위치해있지 않다는 가정으로부터 나온다.
그러므로 이미지의 테두리 부분에 가장 낮은 pixel 값을 부여해줘서 filtration을 만들어, background와 같은 정보들은 테두리의 homology class에 merging해 infinite persistence를 가지도록 만든다.
이렇게 되면 상당히 많은 irrelevant한 object들이 topologically significant 해진다.
이제 이들을 제외하고 finite persistence만 가지는 object만 고려한 뒤, thresholding으로 적당한 persistence 이상을 가지는 영역만 고려하면 중요한 object를 걸러낼 수 있게 된다.
단순히 topologically insignificant한 object만 제거하던 기존의 아이디어와 다름에 유의하자.

Motivation

Image data는 특유의 grid structure 덕분에 TDA를 수행하기 용이하다.
그러나 실제 이미지 내에는 outlier가 많기 때문에 단순히 persistent homology를 사용하는 것으로 원하는 solution을 얻기 어렵다.
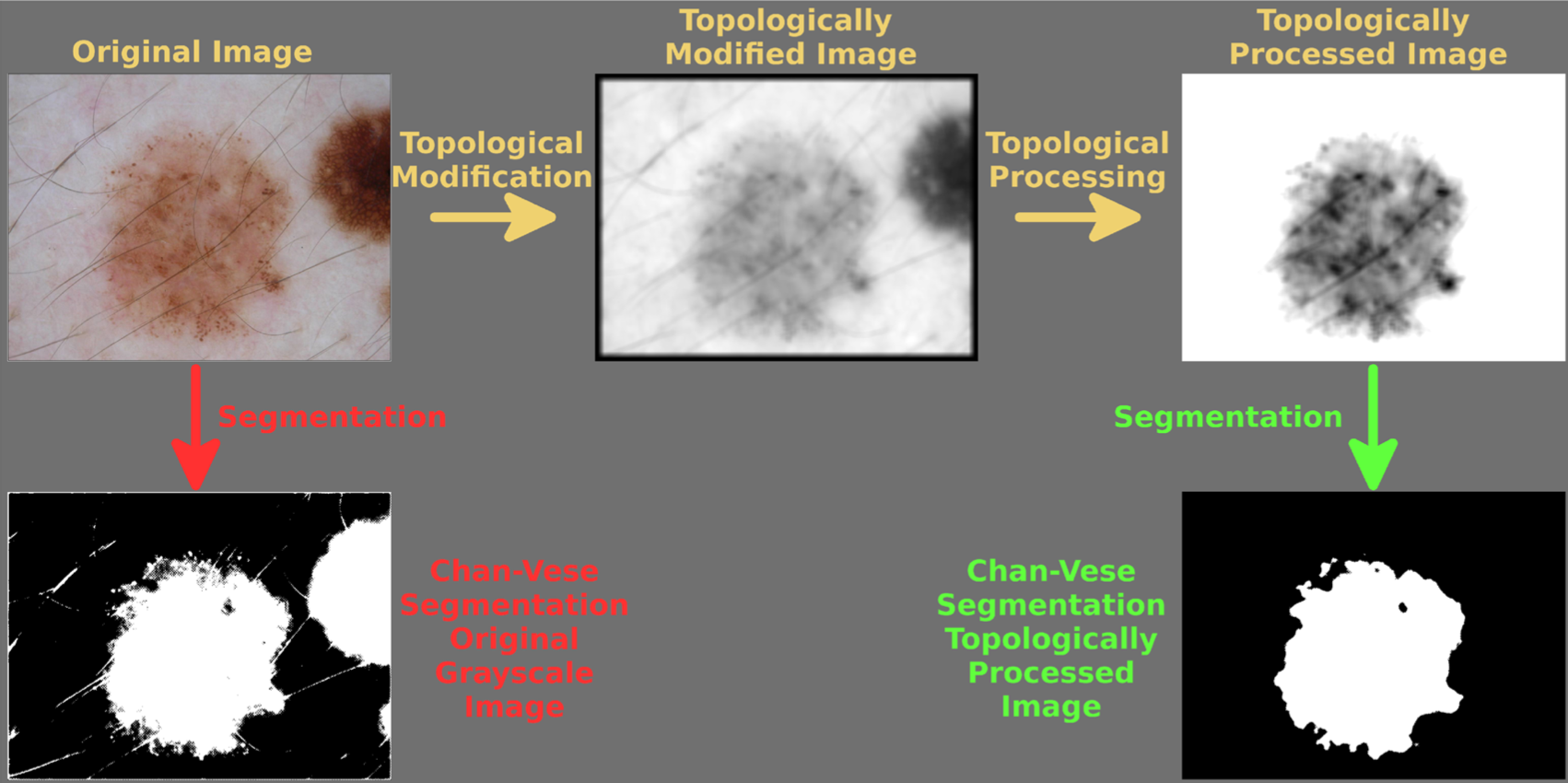
저자들은 이런 상황을 극복하고자 Topological Image Modification (TIM)을 이용해 먼저 이미지를 TDA를 하기 좋게끔 처리한다음 Topological Image Processing (TIP)으로 원하는 작업을 수행한다.
TIM과 TIP의

Methodology

1. Persistent homology of images

이미지 데이터를 분석하기 위해 여기서는 Persistent homology를 사용한다.
Persistent homology로 데이터를 분석하기 위해서는 두 가지의 수학적 개념이 구축되어야 한다.
하나는 이산적인 데이터에 연결성을 부여하는 개념인 simplicial complex $K$ 이고, 다른 하나는 $K$ 의 연결성이 어떻게 진화해나가는지를 보여주는 filtration $\mathcal{F}$ 이다.
Simplicial complex와 filtration에 대한 자세한 내용은 Algebraic topology 교과서를 참고하길 바란다.

$M\times N$ 이미지 $I$가 주어졌다고 하자.
그러면 $I$가 가지는 grid 구조로부터 simplicial complex $K$ 는 자연스럽게 정의된다.
즉, simplicail complex $K$ 는 단순히 이미지가 정의된 grid 위의 각 pixel마다 상하좌우 및 대각선 모든 방향의 8가지 방향에 놓인 픽셀과 edge로 연결하는 것이다.

특이하게 여기서는 일반적으로 TDA에서 이미지 데이터를 다룰때 사용하는 Cubical complex를 사용하지 않고 Simplicial complex를 사용한다.
Cubical complex를 사용할 때는 pixel이 상하좌우 네 가지 방향으로만 연결될 수 있다.
개인적인 의견으로 Simplicial complex가 Cubical complex가 더 디테일한 연결성을 표현할 수 있을진 몰라도 complex를 구성하는 component가 cubical에 비해 월등히 많기 때문에 complexity 면에서 불리하다.
애초에 TDA로 데이터 처리하는 것이 그다지 빠르지 못한데, 이러한 점은 매우 불리하게 작용할 것으로 보인다.
더군다나 image의 resolution이 충분히 커지면 cubical complex를 쓰는 것으로 충분히 detail한 정보를 캐치할 수 있을 것으로 보인다.

이미지 $I$에서 filtration을 구성하기 위해 scale function $f : K \rightarrow \mathbb{R}$를
$\sigma \mapsto \max_{p\in\sigma} gray_I(p)$로 정의한다.
이 함수는 각 simplex마다 그것을 구성하는 pixel들의 grayscale 값 중에서 최댓값을 부여하는 것이다.

RGB 이미지의 경우앤 standard linear converter를 사용하여 다음과 같이 grayscale화하여 동일하게 논리를 전개해나간다.
$gray_I(p) = \frac{1}{1000} (299 red_I(p) + 587 green_I(p) + 114 blue_I(p))$
standard linear converter는 Python PIL 라이브러리에 구현되어 있다.

이제 $f$에 의해 정의되는 sublevel set들로부터 filtration $\mathcal{F} := (\left\{\sigma \in K : f(K) \leq t \right\})_{t\in \mathbb{R}}$을 만들 수 있고, 이를 sublevelset filtration이라고 부른다.

실용적인 목적을 위해서 $\mathcal{F}$에서 유한개 항 $K_0 \subseteq K_1 \subseteq \cdots \subseteq K_n = K$만 고려하자.
각 subcomplex $K_i$에 대응하는 이미지는 $K_i$의 원소인 pixel에는 1을 부여하고 그렇지 않은 pixel에는 0을 부여하여 binary image 형태로 시각화할 수 있다.
이때 $K_i$의 connected component는 값이 1인 픽셀들의 maximal connected cluster이다.

이렇게 이미지를 complex로 표현하고 나면 각 complex의 $k$-th homology를 계산할 수 있다.
$k$-homology의 dimension을 $k$-th Betti number $\beta_k$라고 한다.
Betti number는 complex가 가지는 구멍의 개수를 계산해준다.
0th Betti number는 connected component의 수를, 1st Betti number는 loop의 수를 나타낸다.

Persistent homology는 filtration의 parameter가 증가함에 따라 이러한 구멍들이 탄생하고 죽는 지속성을 정량화할 수 있게 해준다.
또한 Persistent homology로 얻은 정보는 이미지 데이터의 rotation, translation, warping에 invariant하다. 이들 변환은 대상의 위상적인 성질을 변화시키지 않기 때문이다.

Persistent homology가 가지는 또 다른 이점은 noise에 robust하다는 점이다.
이는 Persistent homology의 stability theorem (Cohen)에 따른 것이다.
이 정리는 현재의 상황에서 다음과 같이 해석될 수 있다.

이미지 $I$와 $J$에 대해 이들 각각의 scale function을 $f$와 $g$라고 하자.
$I$와 $J$로부터 얻은 Persistent homology의 차이 (bottleneck distance)는 $f$와 $g$의 차이(infinite norm)로 bound된다.
따라서 두 이미지의 픽셀값의 차이가 작다면 두 이미지의 persistent homology는 유사하다.
예를들어, 이미지 $I$에 약간의 noise를 첨가해 이미지 $J$를 만든다 하더라도 persistent homology는 크게 달라지지 않는다.

Persistent homology를 통해 얻은 정보는 coordinate에 의존하지 않기 때문에, 어디에 있는 어떤 component가 persistence에 대응하는지 알기 어렵다.
그러나, 이미지 데이터의 경우 각 pixel 값이 유일하기 때문에 component의 birth time에 대응하는 pixel 값을 가지는 이미지 내의 component를 추적하면 된다.

2. Topological Image Modification (TIM)

2.1 Image smoothing

이미지의 Persistent homology를 구하기 전에 homology가 잘 계산되도록 image smoothing을 수행한다.
이렇게 해서 pixel 값이 급격하게 변하는 부분을 완만하게 만들어 filtration이 너무 급격하게 변하지 않도록 만든다.
image smoothing을 하는 방법은 CNN 아키텍쳐에서 Average pooling과 매우 유사하다.

1. 홀수 $k$를 고정시키고, 이미지 $I$의 각 픽셀 $p$에 대하여, $k\times k$ 사이즈 neighborhood $\mathcal{N}_k(p)$를 생각하자. 이때 이미지의 영역 밖으로 넘어가는 부분은 정의하지 않도록 한다.
2. 그런 다음 $I$와 동일한 사이즈의 이미지 $I'$를 각 픽셀마다 $\mathcal{N}_k(p)$에 포함된 픽셀들의 grayscale 값의 평균값을 부여한다.

저자들은 hyperparameter $k$를 선택할 때, $\Delta(I)/25$에 가까운 값이 효과적임을 관찰했다.
여기서 $\Delta(I)$는 이미지의 픽셀단위 대각선 길이다.

2.2 Border modification

현실의 이미지에서 persistence가 긴 component가 실제 관심있는 object라고 보장할 수 없다.
여기서 저자들은 기막힌 트릭을 사용한다.
오히려 persistence가 가장 긴 component가 이미지의 중요한 object에 대응하지 않는다고 하는 것이다.

Border modification은 "중요한 object는 적어도 이미지의 테두리(border)와 붙어있지는 않을 것이다"라는 가정에서 위와 같은 아이디어를 구현한 것이다.
이러한 가정은 "중요한 object가 중앙에 놓여있다"는 가정보다 약한 가정이다.
Border modification은 이미지 $I$에서 테두리(border)부분의 pixel 값만 이미지의 가장 낮은 pixel value로 변환하고 나머지는 그대로 놔둔 새로운 이미지 $I_b$를 만드는 것이다.
이렇게 하면 complex가 형성되면서 테두리와 가까이 있는 중요하지 않은 object들은 elder rule에 따라 테두리 component에 흡수될 것이고, 결국 테두리는 infinite persistence를 가지게 된다.
따라서 이후에는 finite persistence에 대해서만 분석하면 이번에는 긴 persistence가 중요한 object를 나타낼 가능성이 더 커지게 된다.