Deep Residual Learning for Image Recognition

• Author: Kaming He, Xiangyu Zhang, Shaoqing Ren, Jian Sun (Microsoft Research)

• Read: 2022년 5월 9일

• Subject: Deep Learning, Computer Vision, Network Architecture, Pattern Recognition

• Submit: 2015년 12월 10일

• URL: https://arxiv.org/abs/1512.03385

Summary

• ISSUE : Neural Net의 Depth가 증가함에 따라 training이 어려워지는 문제가 발생.
• SOLUTION : Residual Learning을 통해 별도의 계산량 변화 없이 효과적으로 Deep Neural Net을 training 시킬 수 있음.

Main Idea

Residual Learning

Machine Learning 문제는 데이터들의 공간 $\mathcal{X}$에서 정답 공간 $\mathcal{Y}$로의 함수 $\mathcal{H}:\mathcal{X} \rightarrow \mathcal{Y}$가 있다고 할 때 sample된 트레이닝 데이터셋 $\mathbf{X} = \left\{(x_i,y_i)\right\}_i^N$로부터 $\mathcal{H}$를 근사시키는 함수 $\tilde{\mathcal{H}}$를 찾는 문제라고 할 수 있다.

예를 들어서 $\mathcal{X}$가 모든 손글씨 숫자 이미지들의 공간이고, $\mathcal{Y}=\left\{0,1,2,3,4,5,6,7,8,9\right\}$라고 하면, $\mathcal{H}$는 손글씨 숫자 $x\in \mathcal{X}$를 입력하면, 그 숫자가 어떤 숫자인지 $y\in\mathcal{Y}$를 말해주는 함수이다.

Deep Learning도 결국은 여러 층의 non-linear layer 구조를 활용하여 함수 $\tilde{\mathcal{H}}$를 만드는 것이다.

여기서 Residual Learning이란, $\mathcal{H}$를 근사하는 문제가 아니라 Residual function $\mathcal{F}(x) = \mathcal{H}(x)-x$를 근사하는 문제로 바꾸는 것이다.

우리는 데이터 $x$를 이미 가지고 있기 때문에 두 문제는 본질적으로 두 문제는 동치이다.

그러나, 이 논문에서 주장하는 것은 Neural Network가 점점 깊어질 수록, $\mathcal{H}$로의 근사는 어려운 반면, $\mathcal{F}$로의 근사는 훨씬 수월하다는 것이다.

Problem Setting : $\mathcal{H} : \mathbb{R}\rightarrow \mathbb{R}$는 $\mathcal{H}(x) = x\sin{x} +x$로 주어져 있다. 이 상황에서 데이터를 sampling해 MLP를 이용해 각각 $\mathcal{H}(x)$와 $\mathcal{H}(x) -x$로 근사시켜보고 MSE를 측정해보자.

$\mathcal{H}(x)$에서 50개의 sample을 얻어 MLP로 학습시켰다.

동일한 sample에서 residual $\mathcal{H}(x)-x$로 동일한 MLP 스트럭쳐로 학습시켰다. MSE 점수가 훨씬 좋다.

Motivation

Deep Learning에서 layer의 depth가 중요한 역할을 하는 것은 일반적으로 잘 알려진 사실이다.

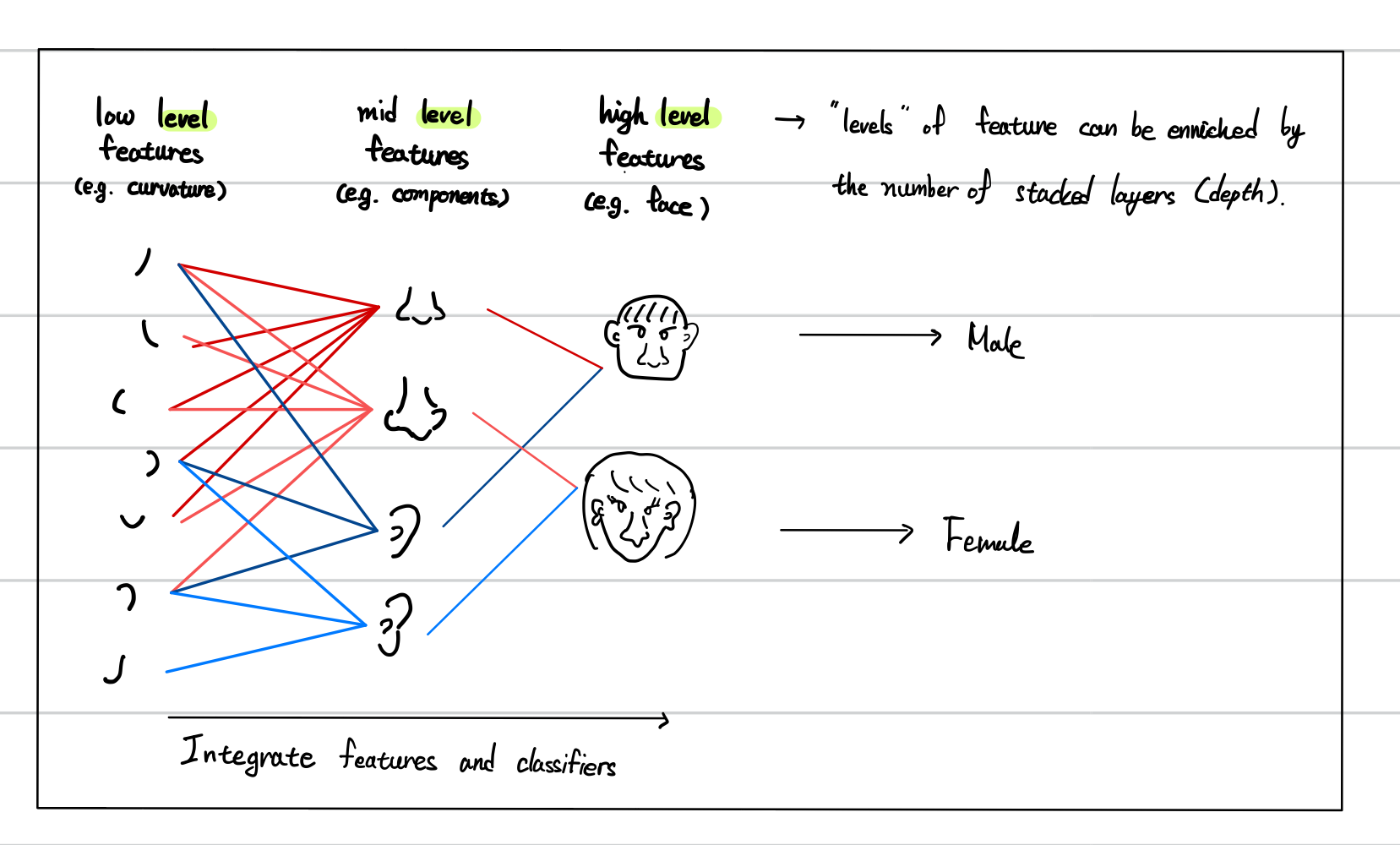
Deep Learning architecture는 얕은 layer에서 깊은 layer로 갈 수록 점차 더 높은 ‘level’의 feature를 학습하기 때문이다.

예를 들어 처음에는 이미지의 curvature와 같은 low level feature를 학습하다가 그 다음 layer에서는 눈, 코, 입, 귀와 같은 middle level feature를 학습하고, 마지막에는 얼굴 형태와 같은 high level feature를 학습하는 식이다.

그러나 불행하게도 Network에 단순히 layer를 쌓는 것은 쉽지만, 그 network가 더 잘 학습할 것이라고는 보장하기 어렵다.

대표적인 장애물은 Gradient vanishing/exploding 문제다.

이 문제에 대해서는 자세히 설명하지 않겠다.

이 문제는 더 나은 initialization 테크닉을 사용하거나, batch normalization과 같은 테크닉을 사용하면 해결할 수 있다.

하지만, 더 큰 문제는 degradation 문제다.

이 문제는 충분히 deep한 model에 layer를 더 추가헀더니 training error가 더 커지는 현상이다.

degradation 문제에 대해서 조금 더 살펴보자.

이 문제는 모든 system이 유사한 난이도로 최적화지는 않다는 것을 시사한다.

예를 들어보자.

shallower network와 그것에 layer를 추가해 얻은 deeper network를 비교한다고 하자.

degradation을 피하려면 deeper network가 최대한 shallower network와 유사하게 작동하면 될 것이다.

그래서 deeper network를 구성할 때, 학습된 shallower network 뒤에 identity mapping layer만 추가해나가도록 구성한다.

이런 구성의 네트워크는 shallower network와 거의 유사한 성능을 보일 것이다.

이런 단순무식한 구성으로 더 깊은 네트워크를 구축했는데 동일한 성능을 보인다면, 분명 더 잘 구성하면 얕은 네트워크보다 좋은 성능을 가지는 네트워크가 존재할 것처럼 보인다.

그러나 수많은 실험에서 이 단순무식한 구성보다 좋은 성능을 보이는 네트워크는 얻어지지 않았다.

이는 degradation이 발생하는 상황은 non-linear layer들을 쌓았어도 이것들이 identity mapping을 잘 근사하지 못함을 시사한다.

이 문제를 해결하기 위해 이 논문에서는 deep residual learning을 제시한다.

deep residual learning은 네트워크가 곧바로 $\mathcal{H}(x)$를 근사하도록 하는것 대신 residual mapping $\mathcal{F}(x) = \mathcal{H}(x) - x$로 근사하도록 만드는 것이다.

그러면 $\mathcal{H}(x) = \mathcal{F}(x)+x$로 표현된다.

저자들의 가설은 $\mathcal{F}$가 $\mathcal{H}$보다 optimize 하기 쉽다는 것이다.

극단적으로는, $\mathcal{H}$가 identity에 가깝다면, residual $\mathcal{F}$를 zero로 만드는 것이 non-linear layer를 쌓아서 identity mapping을 근사시키는 것보다 쉬울 것이다.

Methodology

Residual Learning

$\mathcal{H}(x)$를 stacked layer들(꼭 전체 네트워크일 필요는 없다)로 근사시킬 mapping이라고 하자.

여러 층의 nonlinear layer들이 $\mathcal{H}(x)$로 점근적으로 근사할 수 있다고 가정하자.

그러면 이것은 nonlinear layer들이 residual function $\mathcal{F}(x) = \mathcal{H}(x) - x$로 근사할 수 있는 것과 동치이다. (이때 input과 output의 dimension은 같다고 가정하자)

따라서 문제를 $\mathcal{F}$로의 근사로 생각한다.

두 가지 형태 모두 stacked layer들이 근사할 수 있다는 점은 동일하지만, 학습의 난이도는 다르다.

앞서 살펴본 degradationi problem에서 살펴봤듯, multiple nonlinear layer들이 identity mapping을 근사하는 것을 어려워하기 때문이다.

그러나 만약 $\mathcal{H}$가 identity라면 $\mathcal{F}$를 이용해 근사하는 상황에서는 단순히 layer들의 weight들을 0로 수렴시키는 것으로 $\mathcal{H}$가 identity mapping이 되도록 만들 수 있다.

Identity Mapping by Shortcuts

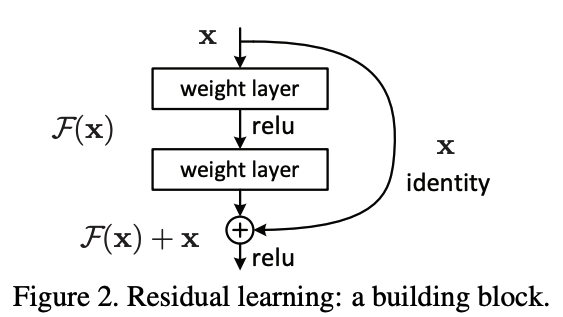
Residual learning은 위 그림으로 도식화된 building block들을 쌓아서 구성된다.

이를 수식으로 표현하면 $\mathbf{y} = \mathcal{F}\left(\mathbf{x},\left\{W_i\right\}\right) + \mathbf{x}$ 이다.

여기서 operator $\mathcal{F}$ 는 $\mathcal{F}=W_2\sigma(W_1\mathbf{x})$로 표현된다. (2층의 mlp 구조, $\sigma$는 ReLU)

이런 구조가 Residual Learning이 되는 이유를 살펴보자.

(Notation이 조금 혼동될 수 있는데 여기서 $\mathcal{F}$는

그냥 $\mathbf{y} = \mathcal{F}\left(\mathbf{x},\left\{W_i\right\}\right)$로 regression 문제를 푼다고 하면, 기존의 MLP 스트럭쳐로 $\mathcal{H}$로 근사시키고 있다고 생각하면 된다.

그런데 layer를 $\mathbf{y} = \mathcal{F}\left(\mathbf{x},\left\{W_i\right\}\right) + \mathbf{x}$로 구성하면 네트워크가 데이터의 layer $y$ 값을 맞추려고 하면서 $\mathcal{F}$에 해당하는 term이 residual인 $\mathcal{H}(x)-x$로 근사하게 될 것이다.

따라서 이런 스트럭쳐는 residual learning이 된다.

특히 주목할 점은 이 네트워크는 기존의 네트워크에서 identity 항 $\mathbf{x}$만 추가했을 뿐, 어떤 파라미터도 추가된게 없기 때문에 모델의 complexity에 영향을 주지 않는다.

일반적인 경우에는 $\mathbf{x}$와 $\mathcal{F}$의 dimension이 다를 때가 많을 것이다.

그런 경우엔, linear projection matrix $W_s$를 사용하여 $\mathbf{y} = \mathcal{F}\left(\mathbf{x},\left\{W_i\right\}\right) + W_s \mathbf{x}$로 네트워크를 구성한다.

위 building block은 2개의 layer로 구성되었지만, 몇 개의 layer를 넣어도 상관없다.

그러나, 1개의 layer를 넣을 경우엔 linear layer가 되어버리므로 2개 이상의 layer로 쌓도록 한다.

지금까지의 설명은 MLP로 했지만, 얼마든지 CNN에서도 적용이 가능하다.