본 포스팅 시리즈는 다양한 머신러닝 테크닉에 대해 수학적 관점과 실용적 관점에서 정리한다.

필자는 수학을 전공했기 때문에 수학적 접근과 용어에 대해 익숙하게 사용한 것이 있지만, 수학을 전공하지 않은 사람들에겐 다소 낯선 접근과 용어가 있을 수 있다.

최대한 그러한 부분을 자세히 설명하려 노력하였지만 필자의 타전공자에 대한 '공감능력부족'으로 효과적으로 전달되지 못한 부분이 있을 것으로 생각된다.

이 글을 읽어주시는 분께 일차적으로 감사드리며, 해당 부분에 대해 질문이나 코멘트를 남겨주시는 분께는 거듭제곱으로 감사드림을 말씀드린다.

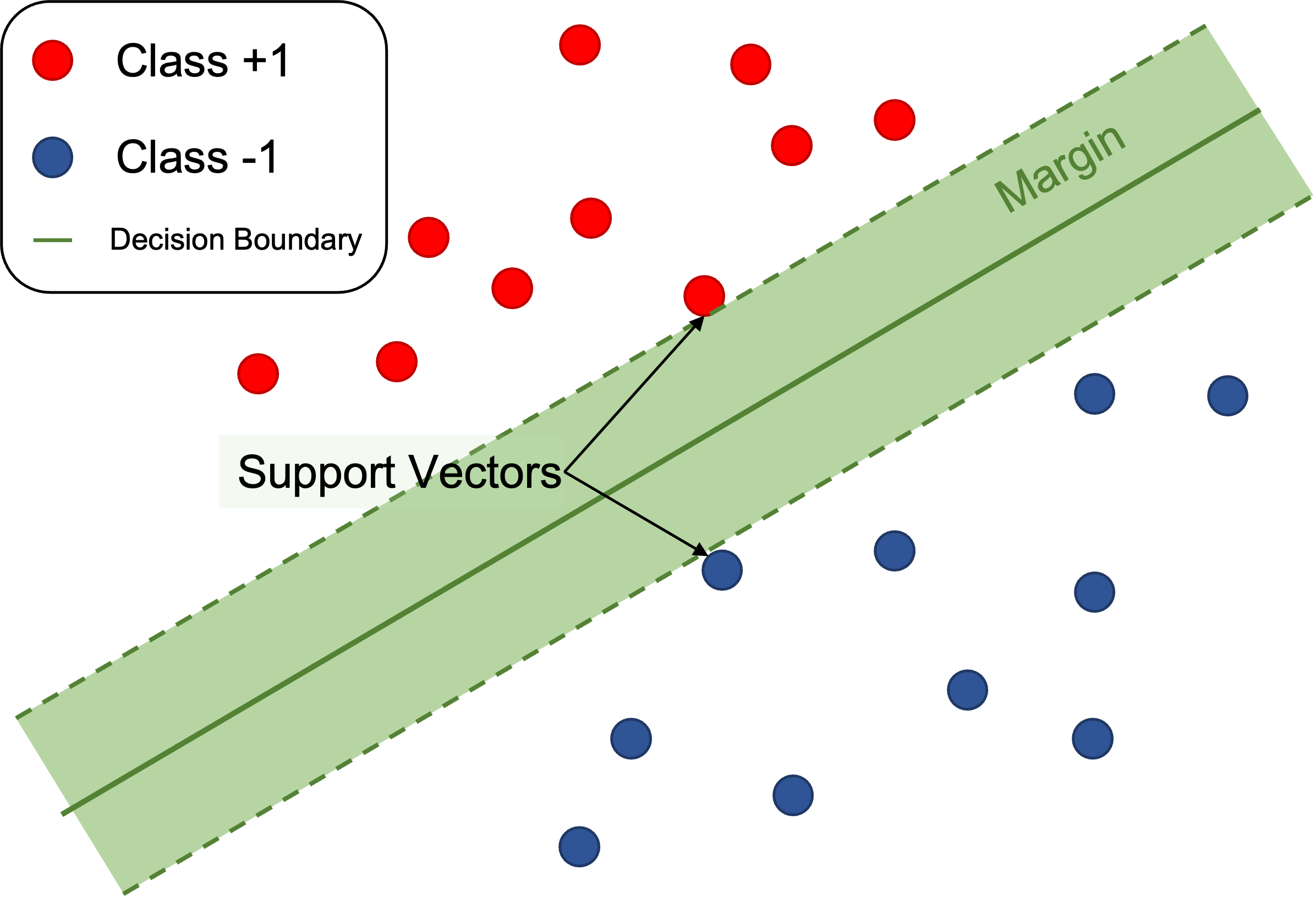
Support Vector Machine

서포트 벡터 머신은 딥러닝이 등장하기 이전에 가장 유명하고 성능 좋은 머신러닝 모델이었다고 한다.
현재는 다소 실무에서 사용되는 정도가 줄어들었겠지만, 서포트 벡터 머신에 적용되는 다양한 수학적 테크닉들은 인공지능을 이해하고 연구하는 데에 여전히 훌륭한 인사이트를 준다고 생각한다.
특히 서포트 벡터 머신의 아이디어는 유클리드 기하학과 최적화 이론으로 설명이 된다는 점은 수학자들에게 있어서 굉장히 매력적이다.

본 포스팅의 내용은 다음의 자료들을 참고했다.

1. Mathematics for Machine Learning (Deisenroth, Marc Peter and Faisal, A. Aldo and Ong, Cheng Soon)
2. The Elements for Statistical Learning (Trevor Hastie, Robert Tibshirani, Jerome Friedman)
3. 김민준님(이화여자대학교, 수학과 석사)의 SVM Lecture note
4. 김원화 교수님(포항공과대학교, 인공지능대학원 교수)의 데이터 마이닝 Lecture note
5. Hands-On Machine Learning with Scikit-Learn, Keras, and Tensorflow (Aurelien, Geron)

4. Hard Margin SVM (2)

이전 포스팅에서는 선형함수 $f(x)$의 방향만 고려하기 위해 제약조건으로 $\lVert \beta \rVert = 1$이 되게 두고 마진 최대화 문제를 유도했다.
만약 선형함수 $f(x)$의 법선벡터 $\beta$가 단위벡터가 아니더라도, 그 크기로 정규화 $(\beta / \lVert \beta \rVert)$해주는 것으로 동일한 문제를 유도할 수 있다.

이번에는 파라미터 벡터 $\beta$를 정규화하는것 대신 단위 또는 기준이 될 데이터를 선택하는 것으로 동일한 문제를 유도해보겠다.
우리가 선텍할 기준은 예측값 $f(x) = x^T \beta + b$의 값이 1이 되는 데이터를 '가장 가까운 데이터'라고 생각하는 것이다.
이러한 데이터를 앞에서와 마찬가지로 $x_a$로 표기하자.
앞에서는 $x_a$에 대해 특별한 가정 없이 '가장 가까운 데이터'로 선택했지만, 이번에는 '가장 가깝다'의 기준을 선형함수 $f(x)$의 값을 기준으로 설정한다는 점에서 차이가 있음에 유의하자.

그러면 $x_a$는 $f(x_a) = 1$을 만족시키므로, 초평면 $\left\{x \in \mathbb{R}^d : f(x) = 1 \right\}$ 위에 놓이게 된다.
이번에도 마찬가지로 $x_a$의 결정경계 위로의 정사영 $x_a'$를 생각한다.
그러면 $x_a'$는 방정식
$f(x_a') = x_a'^T \beta + \beta_0 = 0 \;\; \cdots (1)$
을 만족시킨다.
이때 $\beta$가 앞에서와 달리 단위벡터일 필요가 없음에 유의하자.
한편, 결정경계와 $x_a$ 사이의 거리를 $d$라고 두면 아래의 관계식이 성립한다.
$x_a' = x_a - d\frac{\beta}{\lVert \beta \rVert} \;\; \cdots (2)$
이제 이 식을 위 방정식 (1)에 대입하여 정리하면, 다음 관계식을 얻는다. (유도과정은 연습문제로 남겨둔다.)
$d = \frac{1}{\lVert \beta \rVert} \cdots (3)$

$d$를 이러한 방식으로 유도해주면 모든 $i$에 대하여, $y_i f(x_i) \geq 1$가 되도록 하는 선형함수 $f(x)$를 찾는 문제로 선형분류 문제를 변형할 수 있다.
그러므로 마진 최대화 문제는 다음의 최적화 문제로 정의될 수 있다.
$\max_{\beta, \beta_0} \frac{1}{\lVert \beta \rVert} \\ \text{subject to } y_i(x_i^T\beta + \beta_0) \geq 1, \forall i=1,2,\ldots, N$

이 문제를 계산의 편의를 위해 $\frac{1}{2} \lVert \beta \rVert^2$를 최소화 하는 문제로 변형하자.
이렇게 변형해도 최적해는 변함이 없지만, 해를 구하는 계산과정에서 미분 등의 연산을 할 때 훨씬 편리해진다.
이를 통해 최종적으로 다음의 최적화 문제를 얻는다.

$\min_{\beta, \beta_0} \frac{1}{2}\lVert \beta \rVert^2 \\ \text{subject to } y_i(x_i^T\beta + \beta_0) \geq 1, \forall i=1,2,\ldots, N$

위 최적화 문제는 하드 마진 SVM(Hard margin SVM)이라 부른다.
이 문제를 '하드'하다고 부르는 이유는 이 문제의 유도에서 마진 조건 $y_i(x_i^T\beta + \beta_0) \geq 1$에 조금의 오차도 허용하지 않기 때문이다.
이 문제는 선형 부등식 제약조건을 가지는 컨벡스 최적화 문제로, 라그랑주 승수법을 이용해 해석적으로 풀기에 용이하다.

최소화 형태의 하드 마진 SVM 최적화 문제와 지난 포스팅에서 정의한 최대화 형태의 하드 마진 SVM 최적화 문제는 동치다.
두 문제가 동치임을 보이는 것은 연습문제로 남겨둔다.

이 문제의 해석적 해법에 대해서는 다음에 살펴보도록 하자.

---

연습문제 1)
방정식 (1)에 방정식 (2)를 대입하여 방정식 (3)을 유도하시오.

Solution)

방정식 (1)에 방정식 (2)를 대입하면 다음을 얻는다.
$\left(x_a - d\frac{\beta}{\lVert \beta \rVert}\right)^T \beta + \beta_0 = 0$
그러면 전치연산자 $T$의 성질에 의해,
$\left(x_a^T - d\frac{\beta^T}{\lVert \beta \rVert}\right) \beta + \beta_0 = 0$
임을 얻는다.
그러면 행렬곱의 분배법칙에 의해
$\left(x_a^T \beta - d \frac{\beta^T\beta}{\lVert\beta \rVert}\right) + \beta_0 = 0$
이 성립한다.
이제 위 식을 $(x_a^T\beta + \beta_0) - d\frac{\beta^T\beta}{\lVert\beta \rVert} = 0$
으로 정리하자.

여기서 $x_a$는 $f(x_a) = 1$이 만족하도록 선택했으므로, $x_a^T\beta + \beta_0 = 1$이고 내적의 성질에 의해 $\beta^T \beta = \lVert \beta \rVert^2$ 임을 이용하면,
$1 - d\lVert \beta \rVert = 0$
임을 얻는다.
따라서 이를 정리하면,
$d = \frac{1}{\lVert \beta \rVert} \;\; \cdots (3)$
를 얻는다.

---

연습문제 2)
마진 최대화 문제

$\max_{\beta, \beta_0, d} d \\ \text{subject to } y_i(x_i^T\beta + \beta_0) \geq d, d>0, \forall i=1,2,\ldots, N$
와
파라미터 최소화 문제

$\min_{\beta, \beta_0} \frac{1}{2}\lVert \beta \rVert^2 \\ \text{subject to } y_i(x_i^T\beta + \beta_0) \geq 1, \forall i=1,2,\ldots, N$
가 동치임을 보이시오.

Solution)