들어가며

어제 마음가짐을 다잡고 컨디션이 돌아온게 느껴졌다. 기분도 훨씬 낫고 얼른 무언가를 하고 싶어서 의욕이 넘친다. 그리고 섹션이 시작되면서 만나는 알고리즘. 대부분이 섹션 시작하고 처음 만나는 알고리즘의 난이도가 굉장히 높다고 이야기한다. 다른 파트는 적당히 개념을 알고 넘어가면 되지만 알고리즘은 익숙해질 때까지 꾸준하게 익혀야돼서 단기간에 해결할 수 없다. 이런건 꾸준히 가는 사람이 승리한다. 달려보자.

오늘 배운건 정말 중요한 탐욕 알고리즘과 동적 계획법, Dynamic Programming, DP이다. 알고리즘에 두개의 벽 중 하나로 재귀와 함께 난이도를 올리는 주범이다. 일단... 그렇게 복잡하신 분이니 오늘 하루만에 정복하리라고 생각하진 않는다. 나중에 추가로 정리할 예정.

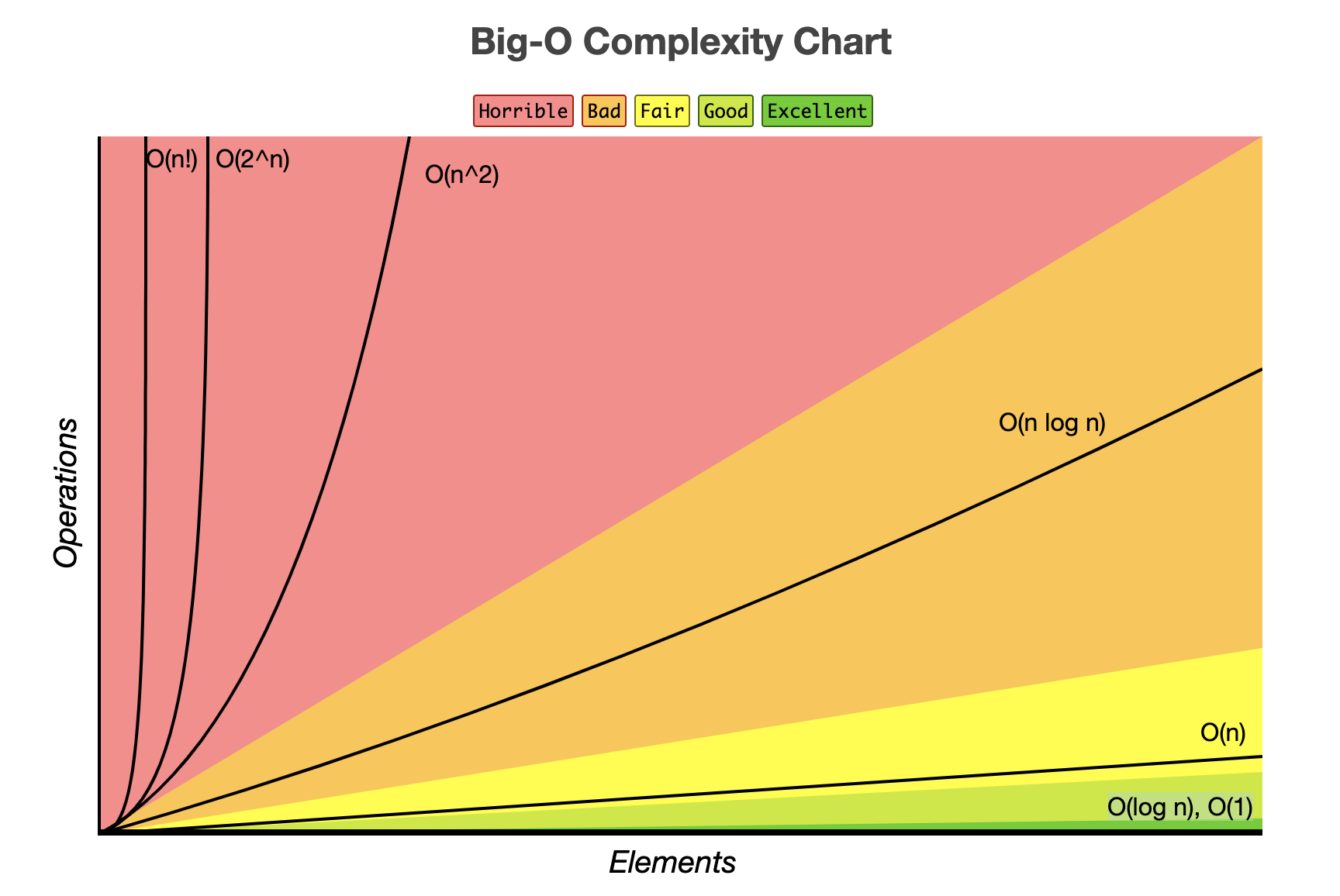
시간복잡도

Toy로 간간히 모습을 보이다가 본격적으로 챕터에 나왔다. 코딩의 시간 효율성을 표기한다. 알고리즘을 풀면 자연스럽게 알게돼서 따로 적을게 없다. 데이터 크기 제한에 따른 알고리즘 선택기준정도? 1억 연산당 1초에 가깝다.

BigO	1초 연산
O(N)	100,000,000
O(NlogN)	5,000,000
O(N^2)	10,000
O(N^3)	500
O(2^N)	26
O(N!)	11

탐욕 알고리즘

Greedy는 "탐욕스러운, 욕심 많은" 이란 뜻입니다. Greedy Algorithm(탐욕 알고리즘)은 말 그대로 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫓아 최종적인 해답에 도달하는 방법입니다. 탐욕 알고리즘으로 문제를 해결하는 방법은 다음과 같이 단계적으로 구분할 수 있습니다.

• 선택 절차(Selection Procedure): 현재 상태에서의 최적의 해답을 선택합니다.
• 적절성 검사(Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사합니다.
• 해답 검사(Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복합니다.

탐욕 알고리즘은 문제를 해결하는 과정에서 매 순간, 최적이라 생각되는 해답(locally optimal solution)을 찾으며, 이를 토대로 최종 문제의 해답(globally optimal solution)에 도달하는 문제 해결 방식입니다. 그러나 도둑의 예와 같이 항상 최적의 결과를 보장하지는 못한다는 점을 명심해야 합니다.

따라서 두 가지의 조건을 만족하는 "특정한 상황" 이 아니면 탐욕 알고리즘은 최적의 해를 보장하지 못합니다. 탐욕 알고리즘을 적용하려면 해결하려는 문제가 다음의 2가지 조건을 성립하여야 합니다.

• 탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않습니다.
• 최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성됩니다.

탐욕 알고리즘은 항상 최적의 결과를 도출하는 것은 아니지만, 어느 정도 최적에 근사한 값을 빠르게 도출할 수 있는 장점이 있습니다. 이 장점으로 인해 탐욕 알고리즘은 근사 알고리즘으로 사용할 수 있습니다.

동적 계획법

Dynamic Programming의 원리는 간단합니다. 주어진 문제를 여러 개의 하위 문제로 나누어 풀고, 하위 문제들의 해결 방법을 결합하여 최종 문제를 해결하는 문제 해결 방식입니다. 하위 문제를 계산한 뒤 그 해결책을 저장하고, 나중에 동일한 하위 문제를 만날 경우 저장된 해결책을 적용해 계산 횟수를 줄입니다. 다시 말해, 하나의 문제는 단 한 번만 풀도록 하는 알고리즘이 바로 이 다이내믹 프로그래밍입니다.

다이내믹 프로그래밍은 다음 두 가지 가정이 만족하는 조건에서 사용할 수 있습니다.

• 큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제가 중복해서 발견된다. (Overlapping Sub-problems)
• 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용할 수 있다. (Optimal Substructure)