데이터 분석 Study -08

Supervised Learning

KNN

Test 데이터와 가까운 k개의 Train데이터의 y값들을 비교

• 분류와 회귀 문제 모두 다룰 수 있다.

• 분류 시 class 다수결로 결과 class 예측

• 회귀 시 평균값을 결과값으로 예측

• 비모수 방식이고 instance-based 알고리즘이다

• Train, Test세트로 데이터를 분리하지만, 실제로 Train은 존재하지 않는 '게으른' 알고리즘이다.

• 구체적인 데이터를 가지고 예측을 요청할 때, K개의 가장 가까운 사례를 Train Data Set에서 찾아 해당하는 데이터의 y값을 기반으로 예측 결과를 제시한다.

• Tell me who your neighbors are, and I'll tell you who you are.

• 이 책을 구매한 사람들이 같이 본 책
  

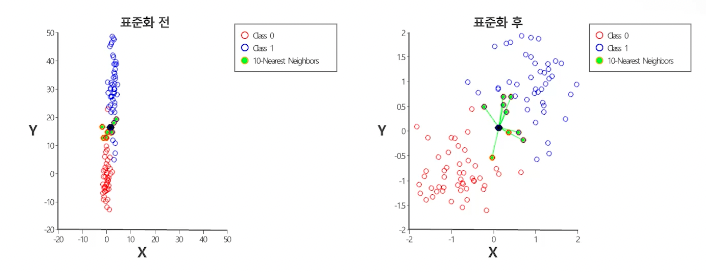
• '거리'개념을 사용하는 알고리즘의 경우 Normalization사용을 항상 검토할 필요가 있다.
  

  나이브베이즈

• Feature들이 확률적으로 '독립'이라는 가정으로 확률 계산을 용이하게 한다.

• 많은 Feature을 사용할 때, Feature간 연관성을 고려하면 너무 복잡해져 독립성을 가정하는 단순화가 효과적으로 문제를 풀 수 있게 한다.

• 결과는 Output class 가운데 가장 높은 확률을 가진 class로 예측한다.

• text 분석에 자주 쓰인다.

• 샘플 데이터가 너무 작으면, 데이터 값이 1만 증가해도 확률값이 너무 크게 변할 수 있기 때문에(overfitting), Laplace Smoothing을 한다.(분모에+2, 분자에+1한다.)

• 가장 단순한 지도학습으로 computation cost가 작고, 적은 량의 데이터로도 높은 정확도를 보여준다. (잡음, 누락에 강함)

• 연속형 보다는 이산형 데이터에서 높은 성능을 보이고 멀티 클래스에서도 사용이 가능하다.

• 각 Feature끼리 독립적이지 않을 수도 있어 문제가 될 수 있다.

• 조건부 확률이 0이 되는 문제가 있어 상수항이 필요할 때가 있다.

• 스팸 메일 필터링, 네트워크 침입, 관찰된 증상에 대한 의학적 질병 판단 등에 활용

의사결정나무

의사결정 규칙(Decision Rule)을 나무 구조로 도식화 하여 관심대상이 되는 집단을 몇개의 소집단으로 분류하거나 예측하는 계량적인 분석 방법이다. If~then형태의 추론규칙으로 표현되기 때문에 다른 분석 방법에 비해 이해가 쉽다.

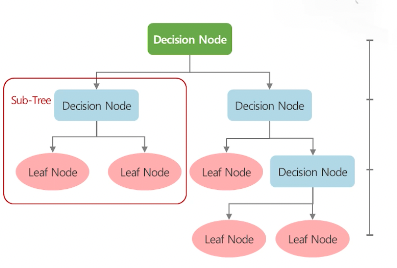
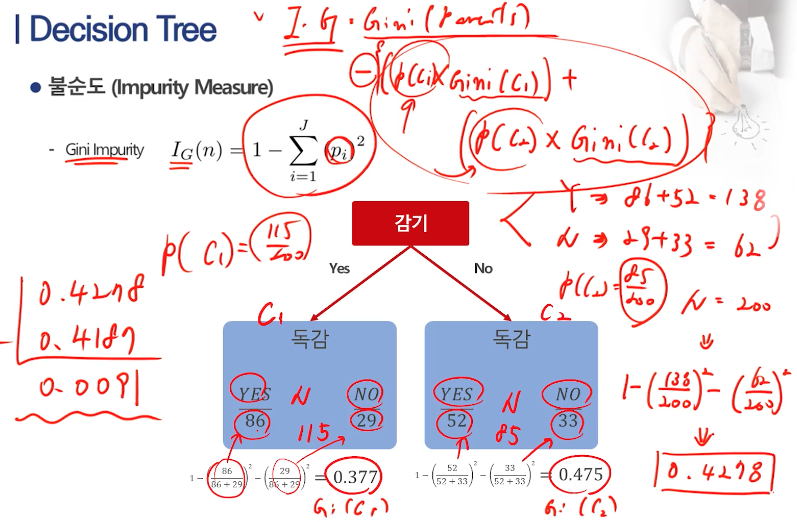
의사결정나무는 불순도를 감소시키는 방향으로 분리되는데, 현재 보고 있는 dataset의 target value가 모두 값은 값이면 stop 된다. (과적합 방지, 혹은 긴 실행시간을 제한하기 위해, tree깊이가 지정한 Max Depth에 도달했거나, 노드 크기가 지정한 값(Min Instance Per Node)보다 작아지거나, 불순도(Min Information Gain)가 지정된 값보다 적으면 stop가능하다.)

• 시각화가 쉽고 자료 가공이 거의 필요 없다.
• 수치형, 범주형 데이터 모두 적용 가능하고, 선형성과 정규성등의 가정이 필요없는 비모수적인 방법이다.
• 대량 데이터 처리에도 적합하다.
• 휴리스틱에 근거한 실용적인 알고리즘으로 전역 최적화를 얻지 못할 수 있다.
• 과적합이 쉽게 발생할 수 있고, Feature간 복잡한 관계 처리가 힘들다.

• 과적합: 새로운 데이터에서 정확한 예측을 하지 못하는 경우 데이터를 더 넣어야 한다.

• 일반적으로 Tree 상단에 있거나, 자주 나오거나, 혼잡도 개선 효과가 높은게 중요하다.

Unsupervised Learning

데이터의 label없이 데이터 특징 만으로 패턴을 찾는 학습 방법. 알려지지 않는 모든 종류의 패턴을 찾고 싶고, 범주화에 도움이 되는 특징과 패턴을 알아내고 싶고, 새로운 데이터를 실시간으로 처리하고 싶고, 데이터 확보를 쉽게 하고 싶을 때 사용한다. (Clustering, Association Rule, Dimension Reduction,,,)

군집분석 (Clustering)

• 계층적 clustering : 최단 연결법, 최장 연결법, 평균 연결법, 와드 연결법

• 비계층적 clustering : k평균 군집화(K-means Clustering, k는 사전에 가정)
  -- K-means Clustering에서 클러스터 갯수를 선정하는 법은 Elbow Method, Silhouette coefficient를 사용한다. 실루엣 갯수는 크게 나오는 것을 선택한다. K-means는 언제나 cluster가 나눠진다. 그리고 이상값에 민감하다.

• clustering은 범주형 데이터는 사용할 수가 없다. 무조건 수치형 데이터만 가능하다. 그리고 표준화가 필요하다. (min-max scaling)