데이터분석 Study 04

상관분석을 통해 선형성을 확인한 뒤에 선형회귀분석을 진행한다. 여기서 상관분석의 전제조건은 독립변수와 종속변수 모두 수치형 데이터라는 점이다. 수치형 데이터이기 때문에 기울기, 절편 등을 구할 수 있었던 것이다. 만약 범주형 데이터로 존재한다면 수치형 데이터로 변환하는 과정이 필요한다. (Like One-hot-encoding, dummy variable(가변수화)...)

회귀분석
상관분석을 통해서는 선형성이 있어도 인과관계를 의미하는 것은 아니다. 인과관계를 확인하는 것은 회귀분석이다. 회귀분석(Regression Analysis)은 관찰된 연속형 변수들에 대해 변수들 사이의 모형을 구한 뒤 적합도를 측정해 내는 분석 방법

• 예측함수의 형태에 따라 - 선형회귀 / 비선형회귀
• 독립변수의 갯수에 따라 - 단순회귀 / 다중회귀
• 종속변수의 갯수에 따라 - 단변량회귀 / 다변량 회귀

선형 회귀 분석은 설명변수(독립변수)가 있을 때, 종속 변수를 예측하고, 설명변수의 영향을 측정, 설명할 수 있다.

정규방정식을 통해 기울기와 절편을 구할 수 있다.

검정통계량

• F검정: 회귀 모형의 통계적 유의성을 검정
• t검정: 개별 독립변수가 종속변수에 유의한 영향을 미치는지 검정
  다중회귀분석의 경우 F검정의 결과 회귀 모형이 통계적으로 유의하다고 판단되면 개별 독립변수에 대한 t검정 유의성을 확인한다.

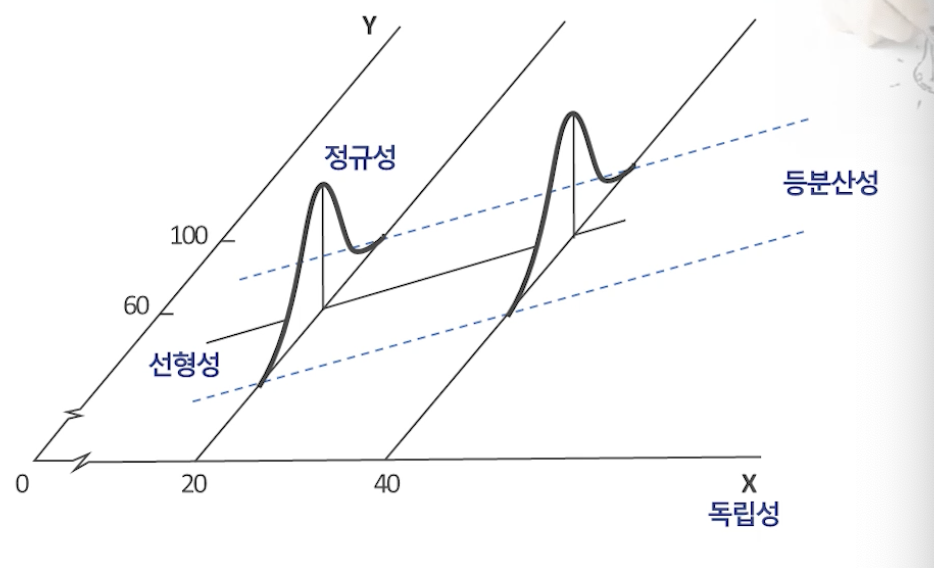
선형회귀분석의 4가지 가정
선형성은 전체 데이터의 분포와 관련이 있고,
정규성, 등분산성, 독립성은 오차에서 사용되는 가정이다.

회귀분석의 가정을 만족하지 못할 때
선형성 이슈

• 산점도 그래프와 회귀선으로 확인
  대응 방법
• 데이터 변환
• 다항 회귀
• 일반화 가법 모형. 함수의 결합으로 표현. 입력데이터를 선형으로 변경시킨다.
  정규성 이슈
• q-q plot으로 확인, kolmogorov-smirnov검점, shapiro-wilk검정 등
  대응 방법
• 데이터 변환
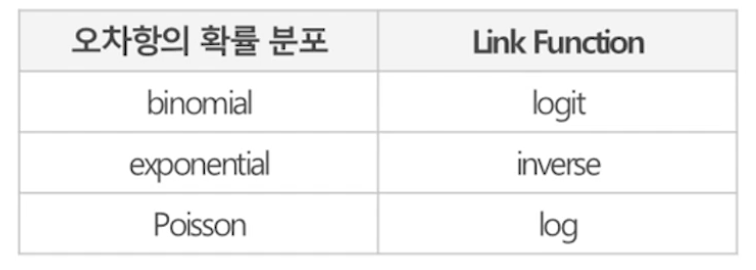
• 일반화 선형 모형(generalized linear model)
• 종속 변수에 변환 함수를 적용하는데, 이를 Link function이라 한다.
  (binomial->logit) (exponential->inverse) (poisson->log)
  등분산성 이슈 - 이상치 때문에
  대응 방법
• 데이터 변환
• 가중 선형 회귀(Weighted Linear Regression/ Weighted Least Square)
• 잔차에 가중치를 적용한 제곱값을 최소화하는 기법
• 가중치는 해당 관측치 분산의 역수. 분산이 작은 관측치는 신뢰하고 분산이 큰 관측치는 신뢰 X
• 관측치 x에 대한 가중치를 일일이 계산해야하므로 연산에 대한 부담이 큰 방법
  독립성 이슈
  오차항이 독립이 아닌 경우, 자기 상관성이 있는 경우, Durbin-Watson통례량으로 확인
• 데이터변환
• 자기회귀모델.(autogressive model)
• 시계열같이 순서가 정해져 있는 데이터에는 주기성이나 계절성 같은 패턴이 자주 나타나며 이런 경우 자기 상관성이 있다고 함
• 시간에 따라 평균이 변하면 - Auto Regressive Moving Average Model
• 시간에 따라 분산이 변하면 - Auto Regressive Conditionally Heteroscedastic Model , Auto Regressive Integrated Moving Average Model

다른 이슈
잔차가 대부분의 데이터와 확연히 차이나는 경우

• 데이터 변환하거나, 잔차의 제곱 대신 절대값의 합이 최소가 되도록 계수 추정하는 방식
• Quantile Regression. 평균이 아닌 특정 분위값 추정. 데이터에도 회귀분석 적용 가능
  *다중공선성-독립변수 간에 강한 상관관계가 있는경우, 상관분석(Variance Inflation Factor)
• Feature Engineering
• Regularization (Ridge Regression(lasso, elastic net), Principal Component Regression, Partial Least Square Regression)
• 잔차 시각화를 통한 회귀분석 가정 검토 - y Actual vs 잔차

• 선형성 : '선형'회귀분석이다. (대응방법:일반화 가법 모형. 설명 변수를 함수화)
• 정규성 : 오차가 정규형태를 갖는다. (Q-Q Plot으로 확인/ 대응방법: 일반화 선형 모형. y값을 함수화)

• 등분산성 : 각 좌표에 대한 오차의 퍼짐의 정도가 비슷하다. (white test로 검토한다./ 대응방법: 가중 선형 회귀. 이상치같은 값 때문에 잔차의 제곱을 역수 시켜 등분산시킨다.)
• 독립성 : 각각의 오차들은 독립적이다. 방향성이 없다. (대응 방법: 자기 회귀 모델)

• 다른 이슈

• Outliers(이상치)의 경우
  1) Robust Regression :절대값의 합이 최소가 되도록 추정하는 방식
  2) Quantile Regression : 구간별로 나눠 선형회귀분석하기
  3) 다중공선성 : 독립변수 간 상관관계가 있는 경우, Feature Engineering, Ridge, Lasso, Elastic net Regulation, Principal Component Regression

R²(결정계수, coefficient of determination)
변수간 영향을 주는 정도 또는 인과 관계의 정도를 정량화해서 나타낸 수치. 추정한 선형의 모형이 주어진 자료에 대해 얼마나 적합한지를 나타낸다.
0<=R²<=1

• 그 외에 MSE(Mean Square Error), MAE(Mean Absolute Error), RMSE(Root Mean Squared Error), MAPE(Mean Absolute Percentage Error)를 통해 성능회귀 모델을 평가할때 사용한다.