Dynamic programming
동적 계획법은 복잡한 문제를 여러 개의 간단한 문제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법을 뜻한다.
핵심 원리
복잡한 문제를 풀기 위해 작은 문제를 풀고, 이때 작은 문제에 대한 정답을 메모해놔야 한다. 한 번 연산했던 결과값을 다시 연산하지 않도록 하는 것이 핵심이다.
동적 계획법의 원리
1. 큰 문제를 작은 문제로 나눈다.
2. 작은 문제들이 반복해서 사용된다.
3. 작은 문제를 연산한 값은 DP 테이블에 저장해서 이를 사용한다.
4. 톱-다운 방식과 바텀-업 방식으로 구현한다.
DP의 핵심은 Memoization이다.
사용 예시 (Java Code)
1. 피보나치 수열
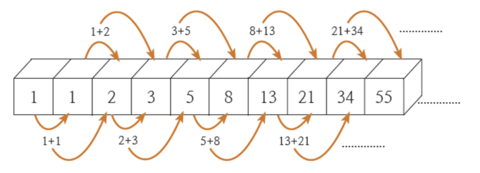
DP의 예시로 가장 많이 사용되는 피보나치 수열이다.
재귀 함수 구현
int fibo(int n){
// System.out.println(n);
return fibo(n-1) + fibo(n-2);
}재귀 함수로는 이렇게 나타낼 수 있다. 코드로써는 보기 편하지만, 실제 컴퓨터의 연산을 찍어보면 내부적으로 많은 연산을 한다. 이때 같은 연산을 반복하는 것도 확인할 수 있는데, 이것이 작은 문제에 해당되는 것이다.
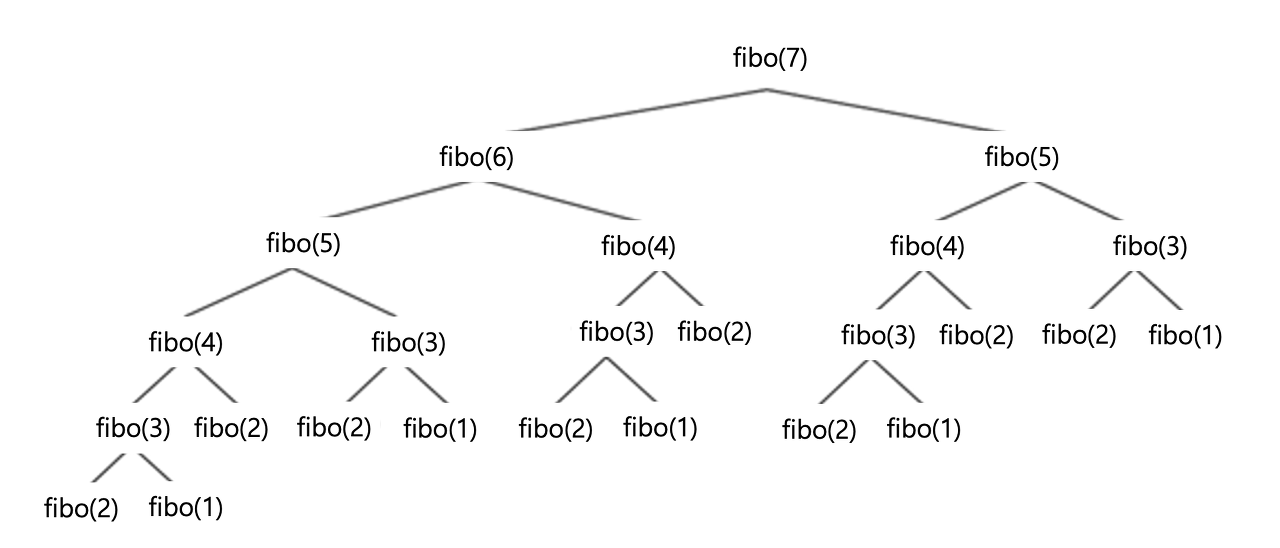
위 사진처럼 피보나치 수열 7번째를 구하기 위해서는 재귀를 탐색하면서 같은 메서드 fibo(2), fibo(1)등을 호출하게 된다.
DP는 이러한 작은 문제를 따로 저장(memoization)하고, 이를 사용하는 방식으로 구현한다.
int dp[] = new int[7]; // -1로 초기화됐다고 가정
dp[0] = 1;
dp[1] = 1;
int fibo(int n){
if(dp[n] == -1) dp[n] = fibo(n-2) + fibo(n-1);
return dp[n];
}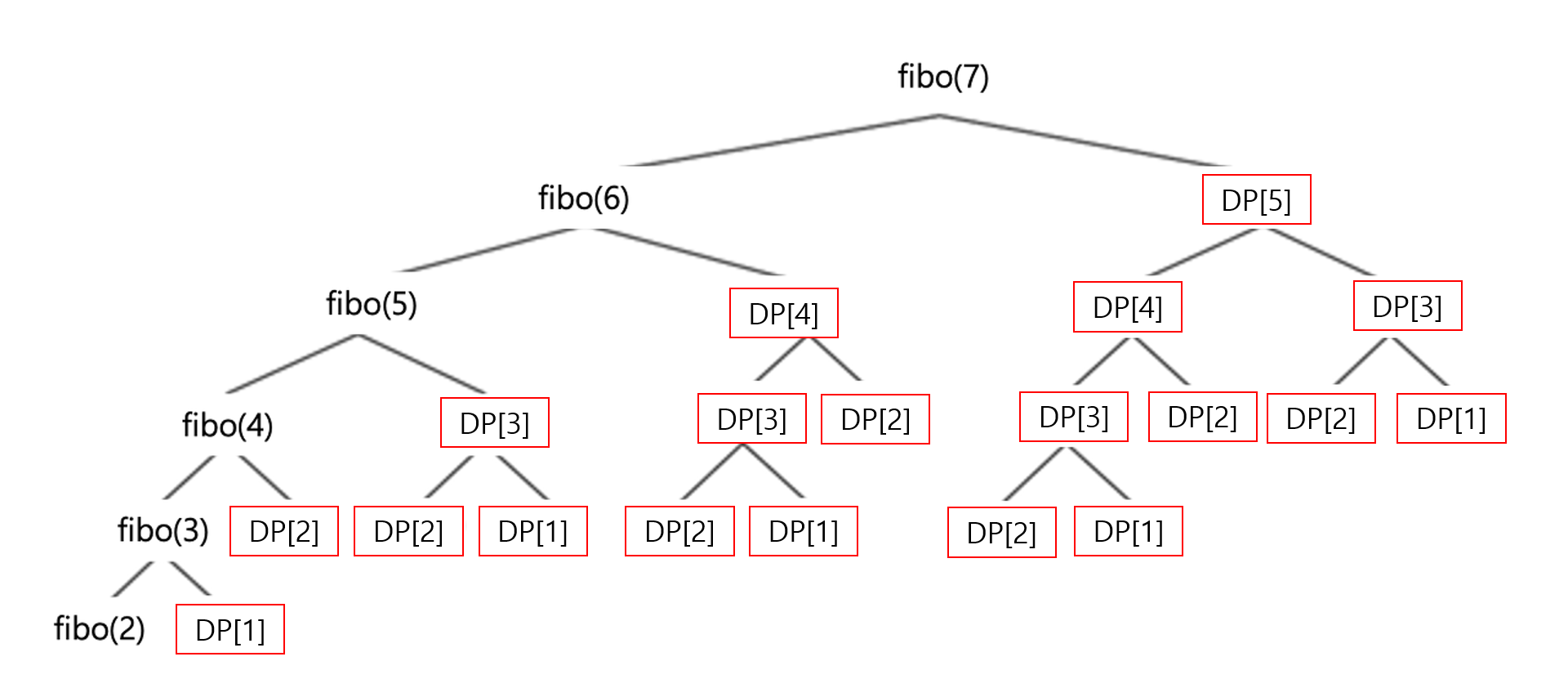
이렇듯 작은 재귀를 통해 호출하는 것은 똑같지만, dp[]에 memoization 된 값이 있다면, 그 값을 return하도록 구현했다. 그러면 내부적으로 재귀 함수의 방문을 확실하게 줄일 수 있다.
참고로 현재 방식은, 정답을 구하기 위해서 dp[7] ~ dp[2]까지 채우는 top-down 방식으로 구현된 것이다. 대부분의 DP 패턴은 이런식으로 작은 문제를 해결하고, 메모이제이션한 뒤 재사용하는 방식으로 진행한다.
2. 돌 게임 (백준 문제)
백준, 실버 V, 9655번 문제
https://www.acmicpc.net/problem/9655
DP 문제 풀이 예시로 가벼운 문제이다.
문제 요약
플레이어가 번갈아가면서 1 또는 3의 돌멩이를 가져갈 수 있을 때, 입력으로 주어진 N을 가져가는 플레이어는 누구인지 구하는 문제이다.
풀이 핵심
N==1또는N==3이라면, 돌멩이는 먼저 게임을 시작한SK가 가져간다.N==2라면, 돌멩이는 늦게 게임을 시작한CY가 가져간다.N번째 돌멩이를 가져가는 사람은N-1또는N-3만큼 돌멩이가 남았을 때 가져간다.
즉,N-1번째 돌멩이를 가져갔을 때 게임이 진행되고 있어야 한다.
이러한 부분으로 게임을 해결하자면 bottom-up 방식으로 구할 수 있다.
구현
public class StoneGame {
static boolean[] dp; // true -> SK 승
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
if (N == 1 || N == 3) {
System.out.println("SK");
return;
} else if (N == 2) {
System.out.println("CY");
return;
}
dp = new boolean[N];
dp[0] = true;
dp[1] = false;
dp[2] = true;
for (int i = 3; i < N; i++) {
// N번째 돌을 가져가기 위해서는 N-1번째 돌에서 게임이 끝나면 안된다.
dp[i] = !dp[i - 1] || !dp[i - 3];
}
if (dp[N - 1]) {
System.out.println("SK");
} else {
System.out.println("CY");
}
}
}3. 1로 만들기 (백준 문제)
백준, 실버 III, 1463번
https://www.acmicpc.net/problem/1463
다른 문제 예시다.
문제 요약
정수 X에 대한 연산은 다음 3가지다.
- X가 3으로 나누어 떨어지면 3으로 나눈다.
- X가 2로 나누어 떨어지면 2로 나눈다.
- 1을 뺀다.
정수 X를 위 3가지 연산을 적절히 사용하여 1로 만들려고 한다. 최소 연산수를 구하라.
풀이 핵심
Bottom-Up 방식으로 DP[] 배열을 채우면 된다. 이때 채우는 방식은 DP[1] ~ DP[N] 까지 증가하면서 비어있는 칸을 3가지 연산으로 채우면 된다.
1 --- 0
2 --- 1 (1 -> 2)
3 --- 1 (1 -> 3)
4 --- 2 (2 -> 4 또는 3 -> 4)
5 --- 3 (4 -> 5)
6 --- 2 (2 -> 6 또는 3 -> 6)
위 내용을 단순하게 나타내자면 다음과 같이 풀 수 있다.
DP[i] = 1 + Math.min(DP[i-1], DP[i/2], DP[i/3])
코드
public class MadeOne {
static Integer[] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
dp = new Integer[N + 1];
dp[1] = 0;
for (int i = 2; i <= N; i++) {
dp[i] = dp[i - 1] + 1;
if (i % 3 == 0) {
dp[i] = Math.min(dp[i], dp[i / 3]+1);
}
if (i % 2 == 0) {
dp[i] = Math.min(dp[i], dp[i / 2] + 1);
}
}
System.out.println(dp[N]);
}
}4. 01 타일 (백준 문제)
백준, 실버 III, 1904번
https://www.acmicpc.net/problem/1904
문제 요약
주어진 타일은 2가지다.
1. 1이라는 1개의 타일
2. 00이라는 2개의 타일이 붙은 하나의 모형
풀이 핵심
점화식을 쉽게 도출할 수 있는 문제이다. 일단 문제에 입력 N에 따라서 숫자를 나열해보자.
1 ---> 1 // 타일 1개
2 ---> 11, 00 // 타일 2개
3 ---> 100, 111, 001 // 여기서 발견할 수 있다.
지금 위에서 발견할 수 있는 것은 3번째에서 알 수 있다.
00에 길이가 2이기 때문에, 1번째에서 1+00을 통해 만들고, 2번째에서는 11+1과 00+1을 만들 수 있다.
즉, 점화식은 다음과 같다.
dp[N] = dp[N-2] + dp[N-1]
구현
public class TileZeroOne {
static long[] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
if (N == 1) {
System.out.println(1);
return;
}
dp = new long[N + 1];
dp[1] = 1; // 1
dp[2] = 2; // 11 00
for (int i = 3; i < N + 1; i++) {
dp[i] = (dp[i - 2] + dp[i - 1]) % 15746;
}
System.out.println(dp[N]);
}
}5. 퇴사 (백준 문제)
백준, 실버 III, 14501번
https://www.acmicpc.net/problem/14501
문제 요약

조건에 맞게 최대 수익을 구하여라.
- 1일 + 4일 + 5일이 최대이다.
- 6일과 7일만 봤을 때에는 수익이 0원이다.
지금은 연습이기 때문에 DP 카테고리를 보고 dp[]를 어떻게 채울까 고민할 수 있었다.
풀이 핵심
해당 로직에서는 1일 + 4일 + 5일이 합쳐진 부분이 정답이된다.
만약 1,2,3일이 없었다면, 4일 입장에서 최대는 몇 일까?
4일에 입장에서 최대 크기도 4일 + 5일인 경우이다.
즉, dp[1]을 구하려면 1일의 요금인 10 + Math.max(dp[4], dp[5], dp[6], dp[7])이 되는 것이다.
이를 구현하기 위해서는 dp[1]에 입장에서 dp[4]~dp[7]이 얼마가 들어있는지 알아야 하므로, top-down 방식으로 dp[]배열을 채웠다.
구현
public class Resignation {
static Integer[] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
dp = new Integer[N + 1];
int answer = 0;
StringTokenizer st;
int meeting[][] = new int[2][N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
int T = Integer.parseInt(st.nextToken());
int P = Integer.parseInt(st.nextToken());
meeting[0][i] = T;
meeting[1][i] = P;
}
for (int i = N; i > 0; i--) {
int T = meeting[0][i - 1];
int P = meeting[1][i - 1];
dp[i] = 0;
if (i + T <= N + 1) {
dp[i] += P;
}
int max = dp[i];
for (int j = i + T; j < N + 1; j++) {
max = Math.max(max, dp[i] + dp[j]);
}
dp[i] = max;
answer = Math.max(answer, max);
}
System.out.println(answer);
}
}마치며
동적 계획법이란 무엇인지 처음 입문할 때, 배운 이론과 감을 잡는데 나에게 도움을 줬던 쉬운 문제들을 나열해봤다.
사실 정말 쉽고 혼자 고민해서 결과를 도출할 수 있었던 문제들만 나열했을 뿐 아직 점화식을 찾는법이나 카테고리가 없는 문제를 보고 DP로 풀이해야겠다는 것을 떠올리기에는 부족한 실력이다.
더욱 연습해서 DP 알고리즘도 자유롭게 풀 수 있도록 해야겠다.

