플로이드-워셜(Floyd-Warshall) 알고리즘
모든 노드 간의 최단 경로를 구하는 알고리즘
- 음의 간선이 포함되어 있어도 사용 가능
- 음수 사이클 발생 시 알고리즘이 정상 종료되지 않으며 올바른 최단 거리를 구할 수 없음
- 다익스트라는 출발점이 한 개로 정해져있고 플로이드-워셜을 출발점이 정해져있지 않고 모든 노드가 출발점이 됨
- 시간 복잡도 : O(V³)
동작 방식
- 초기 거리 행렬 설정
모든 정점i != j에 대해dis[i][j] = ∞,dis[i][j] = 0으로 초기화
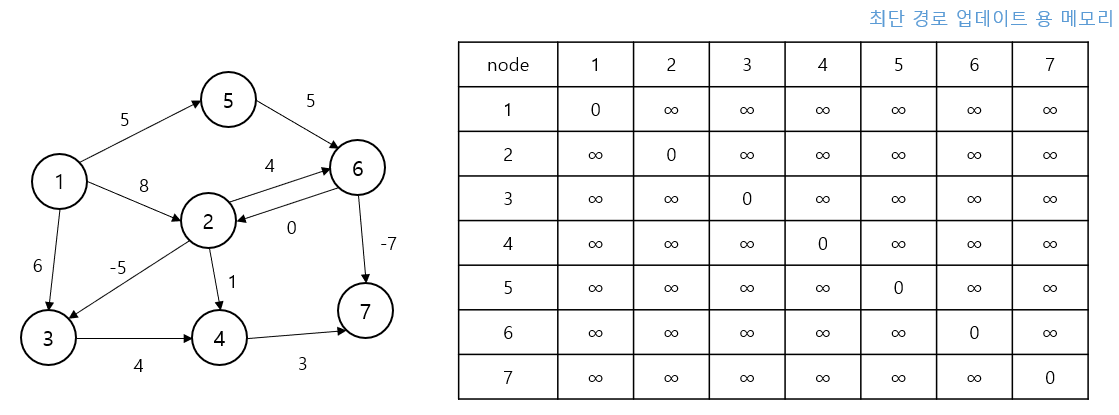
k=1(정점 1) 경유
“정점 1을 거쳐서” 모든 i -> j 경로를 검토
1번에서만 나가는 간선(1 -> 2, 1 -> 3, 1 -> 5)이 있으므로 이들 경로로부터 다른 곳으로 가는 더 짧은 루트는 아직 없음
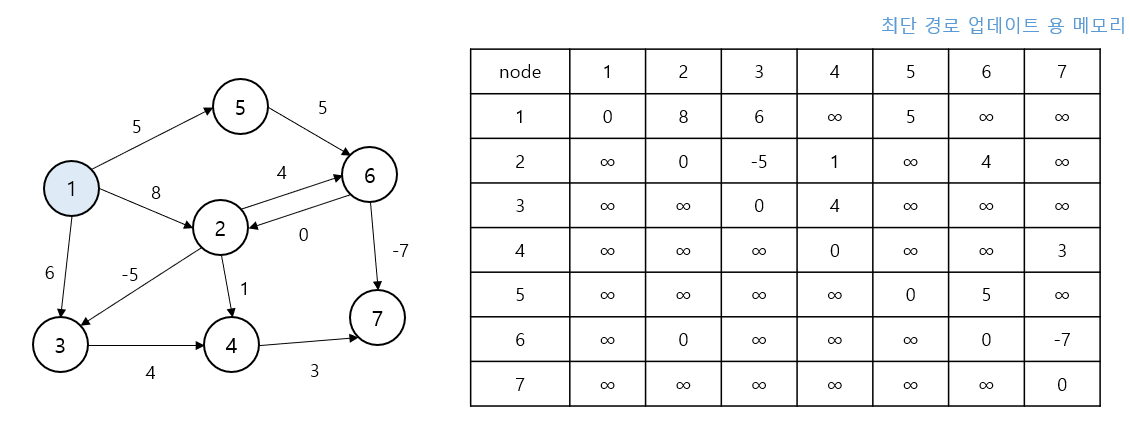
k=2(정점 2) 경유
“정점 2를 거쳐서” 모든 𝑖 -> 𝑗 경로를 다시 검사
특히 1 -> 3 경로가 기존 6에서 1 -> 2 -> 3 (8 + (-5) = 3)으로 단축되어dis[1][3] = 3으로 갱신됨
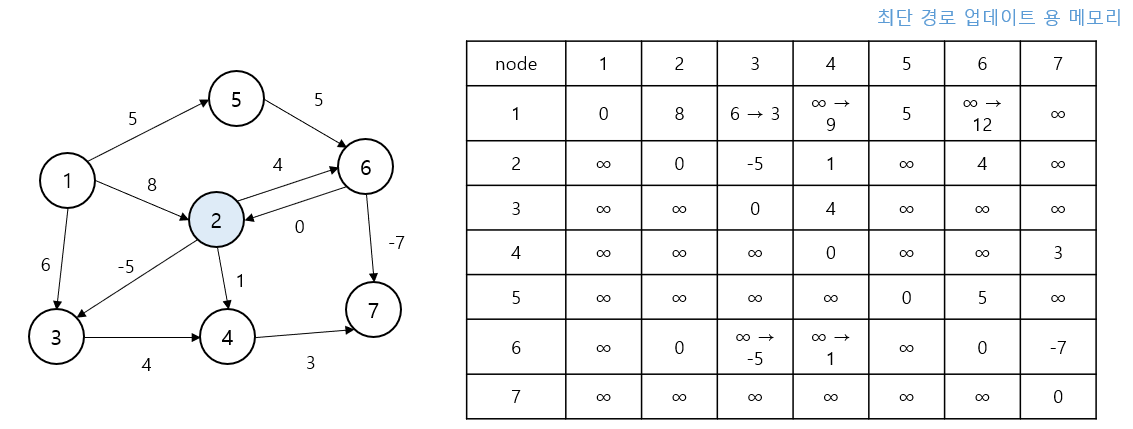
k=3(정점 3) 경유
“정점 3을 거쳐서” 경로 탐색
이제 1 -> 4 경로가 1 -> 3 -> 4 (3 + 4 = 7)로 갱신되어dis[1][4] = 7이 됨
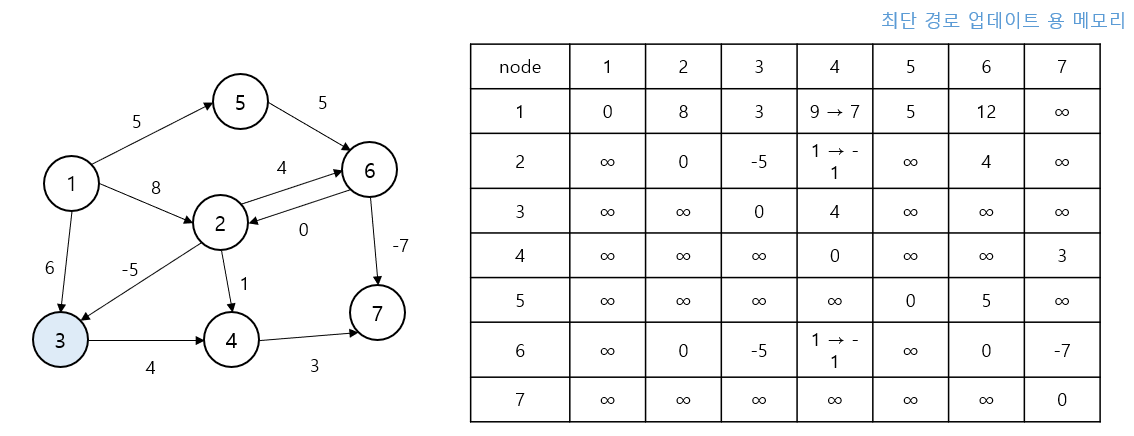
k=4(정점 4) 경유
“정점 4를 거쳐서” 경로 탐색
1 -> 7 경로가 1 -> 4 -> 7 (7 + 3 = 10)으로 단축되어dis[1][7] = 10으로 갱신됨
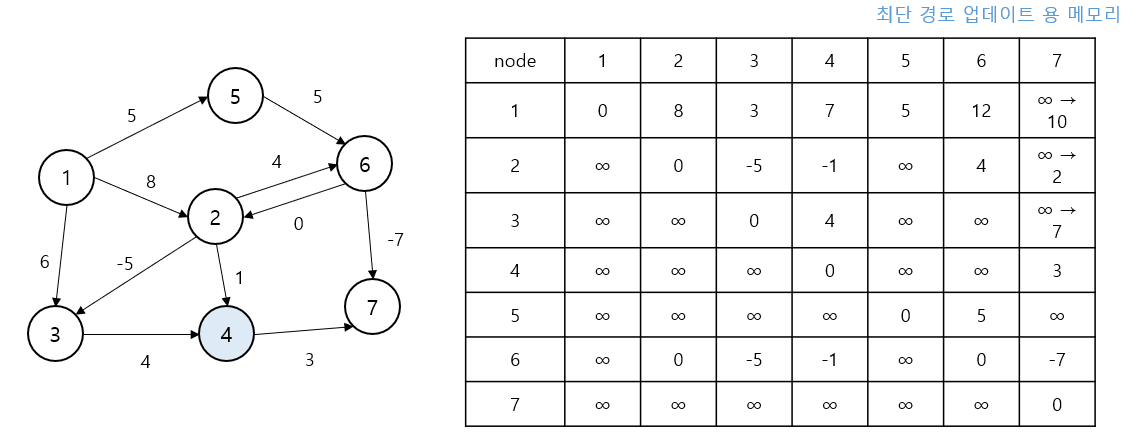
k=5(정점 5) 경유
“정점 5를 거쳐서” 경로 탐색
1 -> 6 경로가 1 -> 5 -> 6 (5 + 5 = 10)으로 갱신되어dis[1][6] = 10이 됩니다.
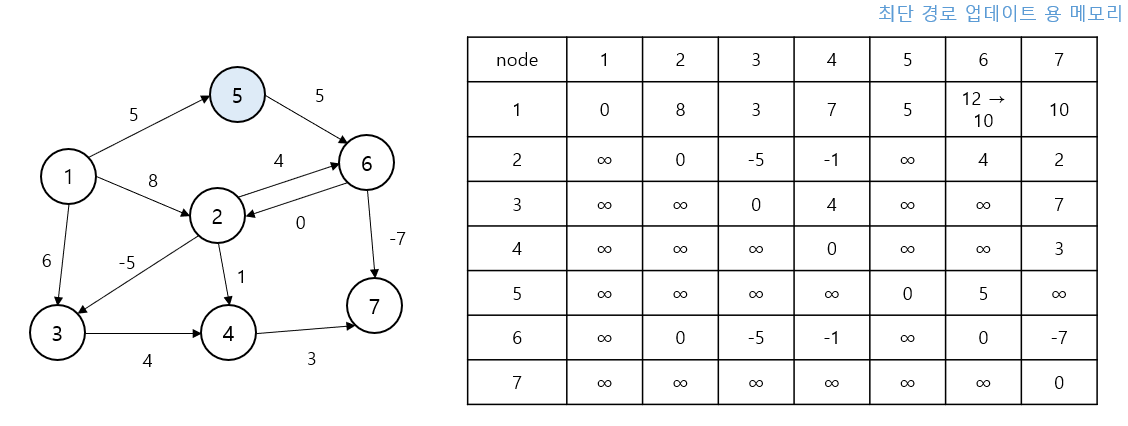
k=6(정점 6) 경유
“정점 6을 거쳐서” 경로 탐색
2 -> 7 경로가 2 -> 6 -> 7 (4 + (−7) = −3)으로 갱신되어dis[2][7] = −3
1 -> 7도 1 -> 6 -> 7(10 + (−7) = 3)으로 추가 단축되어dis[1][7] = 3으로 바뀜
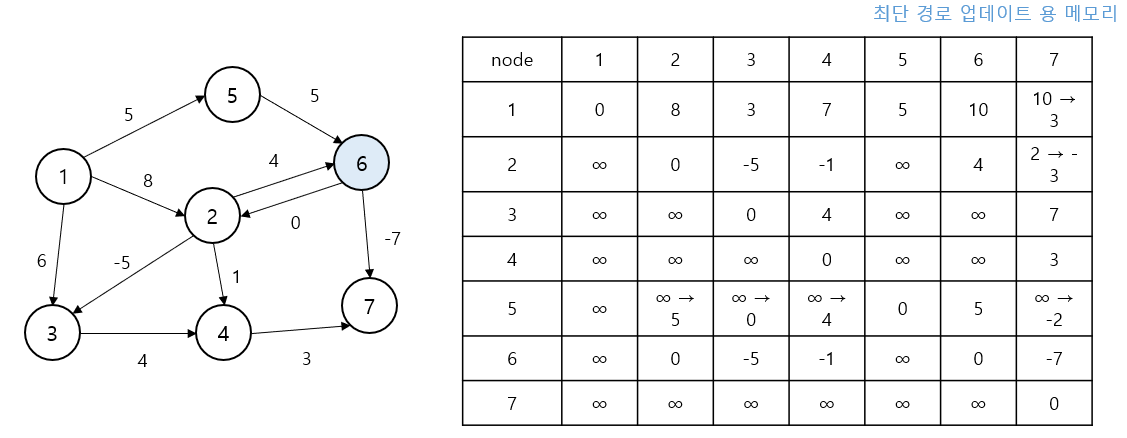
k=7(정점 7) 경유 및 최종 확정
“정점 7을 거쳐서” 마지막 검토
더 이상 어떤dis[i][j]도 짧아지지 않으므로 현재 행렬이 모든 쌍 최단 경로가 맞다는 것이 확정됨
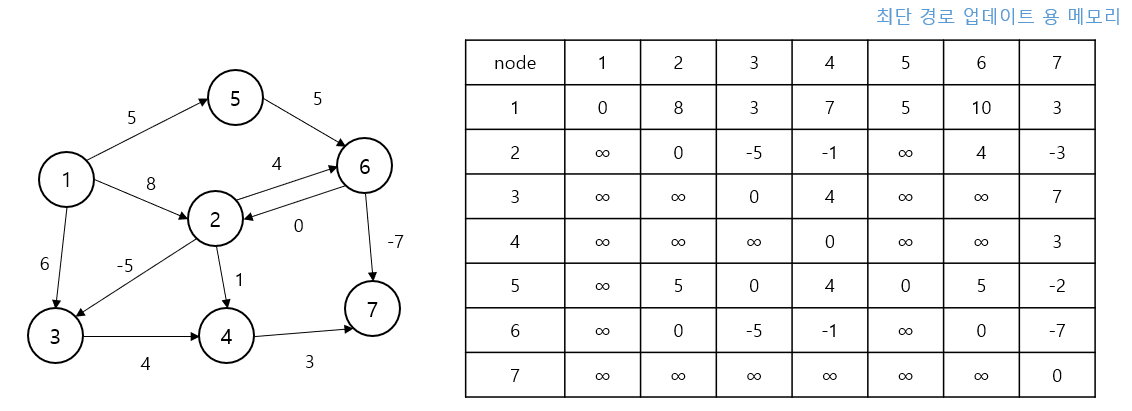
구현 방법
public class Main {
static int[][] dis;
static int INF = 1000000000;
static void floydWarshall(int v, int e, int[][] data, int start) {
dis = new int[v + 1][v + 1];
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++) {
if (i != j) {
dis[i][j] = INF;
}
}
}
for (int i = 0; i < e; i++) {
dis[data[i][0]][data[i][1]] = data[i][2];
}
for (int k = 1; k <= v; k++) {
// i -> j (k를 거쳐서 가는 경우가 짧을 때 업데이트)
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++) {
if (dis[i][k] != INF && dis[k][j] != INF) {
dis[i][j] = Math.min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}
}
for (int i = 1; i <= v; i++) {
for (int j = 1; j <= v; j++) {
if (dis[i][j] >= INF) {
System.out.printf("%5s ", "INF");
} else {
System.out.printf("%5d ", dis[i][j]);
}
}
System.out.println();
}
}
public static void main(String[] args) {
int[][] data = {
{1, 2, 8}, {1, 3, 6}, {1, 5, 5}, {2, 3, -5}, {2, 4, 1},
{2, 6, 4}, {3, 4, 4}, {4, 7, 3}, {5, 6, 5}, {6, 2, 0},{6, 7, -7}
};
floydWarshall(7, 11, data, 1);
data = new int[][]{
{1, 2, 8}, {1, 3, 6}, {1, 5, 5}, {2, 3, -5}, {2, 4, 1},
{2, 6, 4}, {3, 4, 4}, {4, 7, 3}, {5, 6, 5}, {6, 2, -5},{6, 7, -7}
};
floydWarshall(7, 11, data, 1);
}
}