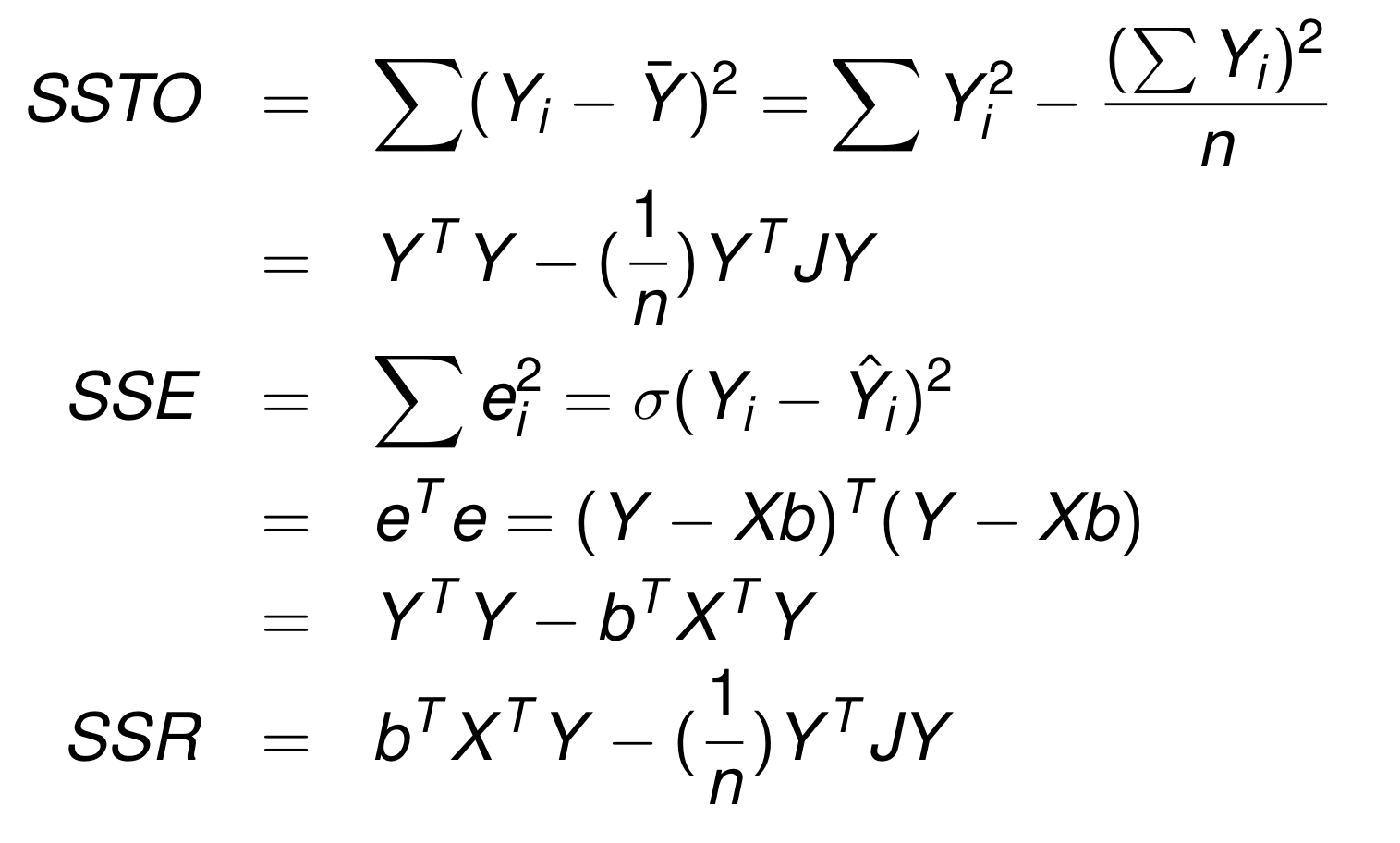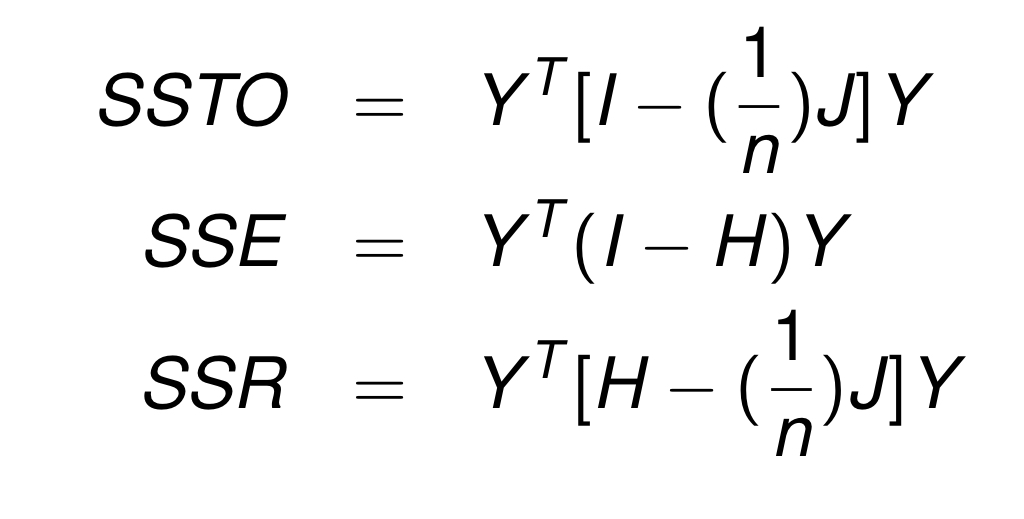Simple linear regression model in matrix form

자, 우리의 목표는 LSE를 통해 계수를 추정하는 것이다. matrix form으로 나타내면 다음과 같이 확인할 수 있다.

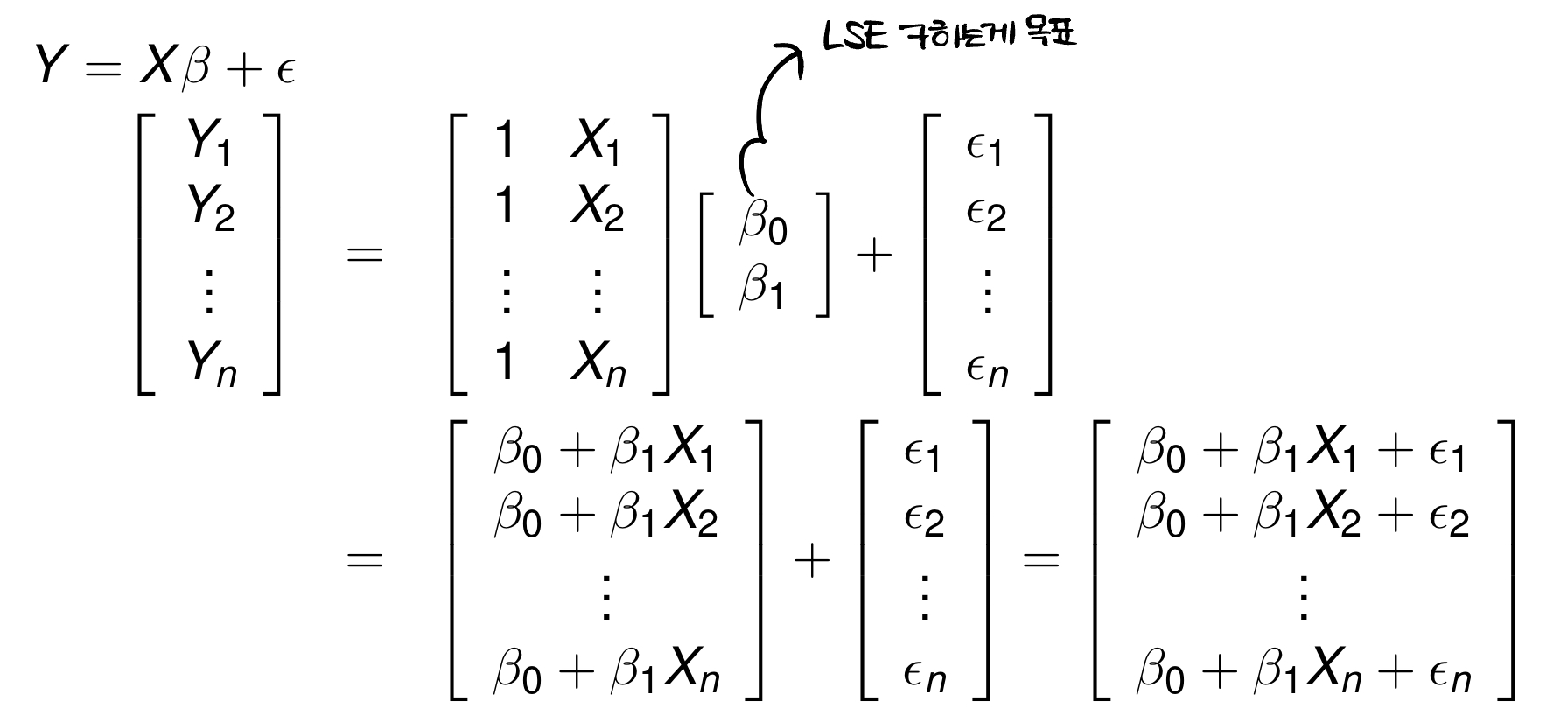
주목할 점으로는 $\mathit{\epsilon}$이 independent한 normal random variables라는 것이다. 그래서 $E(\mathit{\epsilon})=0$이고 $\mathit{\sigma}^2(\mathit{\epsilon}) = \mathit{\sigma}^2I$라는 것이다.

그럼 LSE 정규방정식에 대해서 생각해보자. 이해가 안된다면 이전 포스팅을 참고하면 된다.

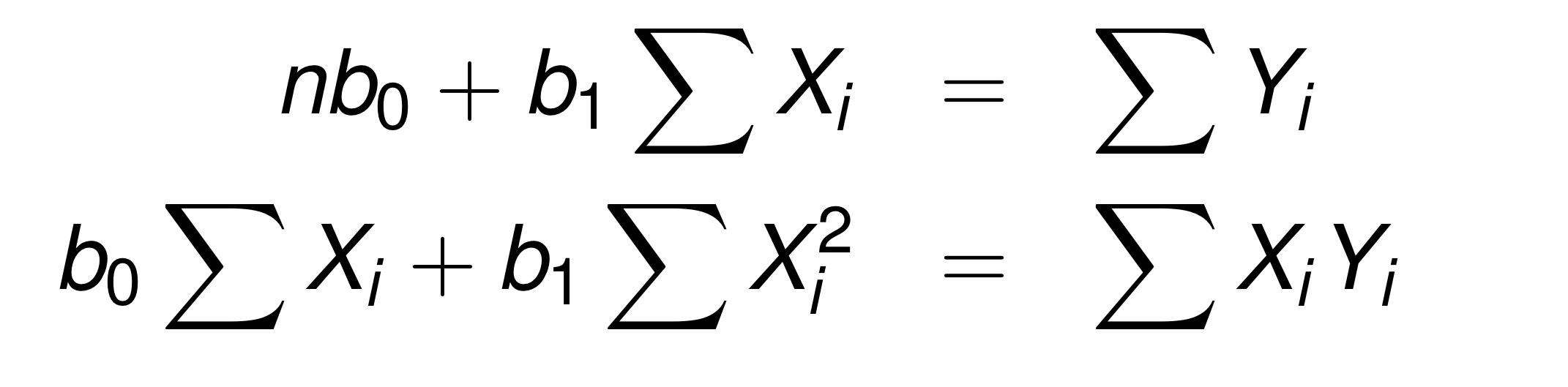
행렬 표현으로 나타내보면, $X^TXb = X^TY$라고 표현할 수도 있다.
우리가 구하고 싶은 것은 $b$이므로, 위 식을 $b$에 대해서 표현해볼 수 있다.

LSE of $\mathit{\beta}$
$b = (X^TX)^{-1}X^TY$

그럼, 정규방정식에서 Y에서 Y를 추정한 값을 빼고, 제곱을 한 뒤 미분을 해서 최솟값을 찾았다! 이번에도 똑같이 적용해보자.

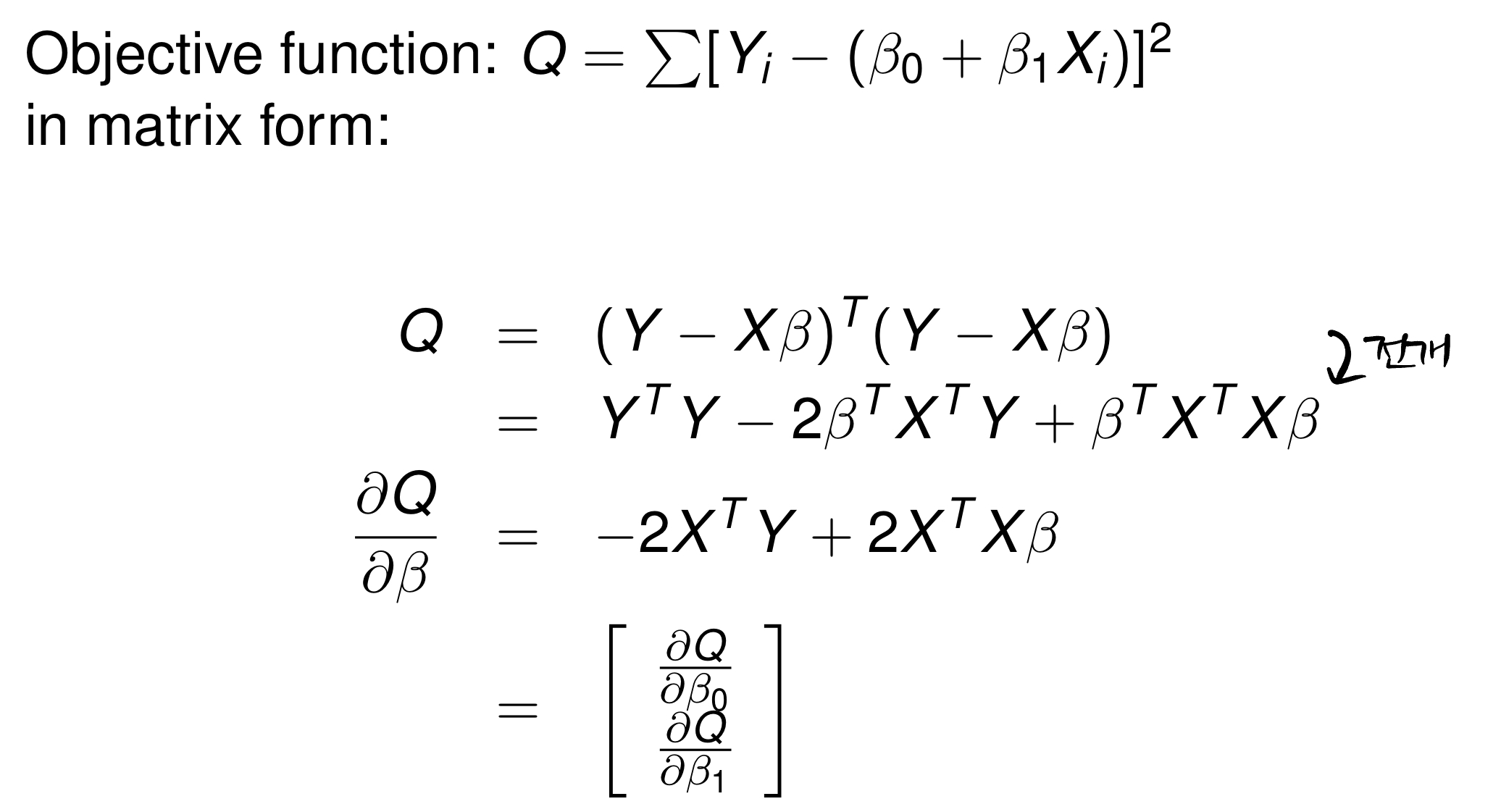
위와 같은 결과를 얻을 수 있다!
우리가 앞에서 다룬 LSE와 정규방정식을 미분한 것 과 같은 결과이지만, 행렬로 표시했을 때 어떻게 되는지를 잘 봐두면 다중회귀가 편안해진다.

Idempotent

idempotent하면 할말이 정말 많아지지만 간략히 하고 넘어가겠다. (TMI : idempotent의 짝꿍인 nilpotent도 있음)
idempotent는 다음과 같이 정의한다.

쉽게 말해서 자기 자신을 제곱해서 다시 자기자신이 나오는 것이다.

Hat matrix

hat matrix의 정의는 다음과 같다.

hat matrix는 위에서 말한 idempotent한 녀석이다. 그 과정을 확인해보자!

$HH = X(X^TX)^{-1}X(X^TX)^{-1}X^T = XI(X^TX)^{-1}X^T = H$
그래서, hat matrix는 symmetric 하다는 것을 쉽게 알 수 있다~!

Residuals

residual을 표현하면 다음과 같다.
$e = Y - \hat{Y} = Y - Xb = Y -HY = (I-H)Y$

또, variance 를 살펴보면 다음과 같다.

$\mathit{\sigma}^2(e) = \mathit{\sigma}^2(I-H)$

이것의 증명은, 대학원에 진학해서 알 수 있다고 한다..

ANOVA Table 살펴보기

행렬로 표현한 anova table 표현에 익숙해져보자! 다음을 참고하면 된다!