multiple regression을 하기 위해서는 행렬과 선형대수 관련 내용을 필수적으로 알고 있어야 한다. 이번 포스팅에서는 행렬 관련한 간단한 지식들을 다룰 예정이다.

최근에 너무 바빠서 글을 잘 작성하지 못했다... 지금도 사실 할 일이 계속 있는데... 그래도 이번주에 너무 포스팅을 하지 않아서 조금씩 해보려고 한다!

Matrix의 정의

: 원소를 직사각형 모양을 행과 열로 나열한 것

요렇게 표현이 가능하다.

square matrix : 정사각 행렬, 행의 num과 열의 num이 같다.

column vector : 열이 하나만 있는 matrix

Row vector : 행이 하나만 있는 matrix

Transpose 란?

matrix에서 행과 열을 바꾸는 것.
다음과 같이 표현할 수 있다.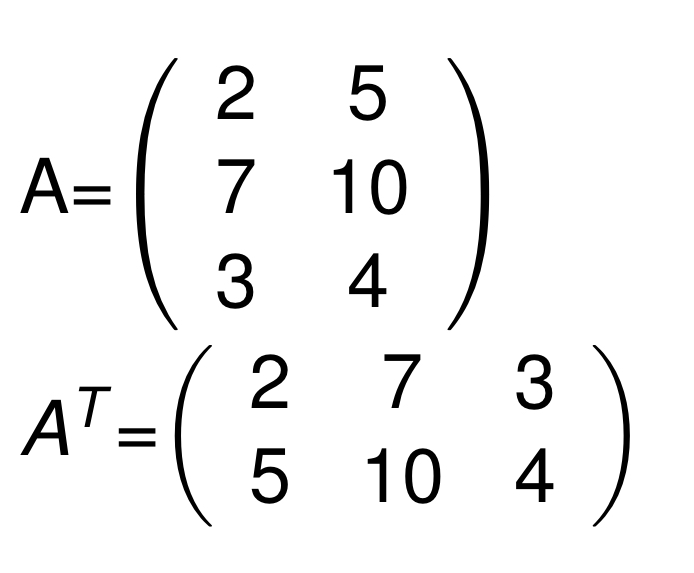

일반적으로 쓰면, $A = (a_{ij})$ 이고 $A^T = (A_{ji})$ 이다.

이제, matrix를 이용해 SLR (simple linear regression) 을 표현해보자!

Matrix apporach to SLR

regression example을 살펴보자.
우선 Design matrix의 구조에 대해 이해할 필요가 있다.

Design matrix란? : 맨 첫번째 열이 1로만 구성된 행렬이다.이는 intercept를 표현하기 위함으로 존재하는 것이고, 전체 predictor수에 1을 더한 것이 행의 수가 된다.

Matrix addition and subtraction

더하기, 빼기와 같은 구조에서는 단순히 같은 위치일때 더하고, 빼면 된다!
$A = (a_{ij})$, $B=(b_{ij})$ 일때 $A+B = (a_{ij}+b_{ij}) , A-B = (a_{ij}-b_{ij})$

ex

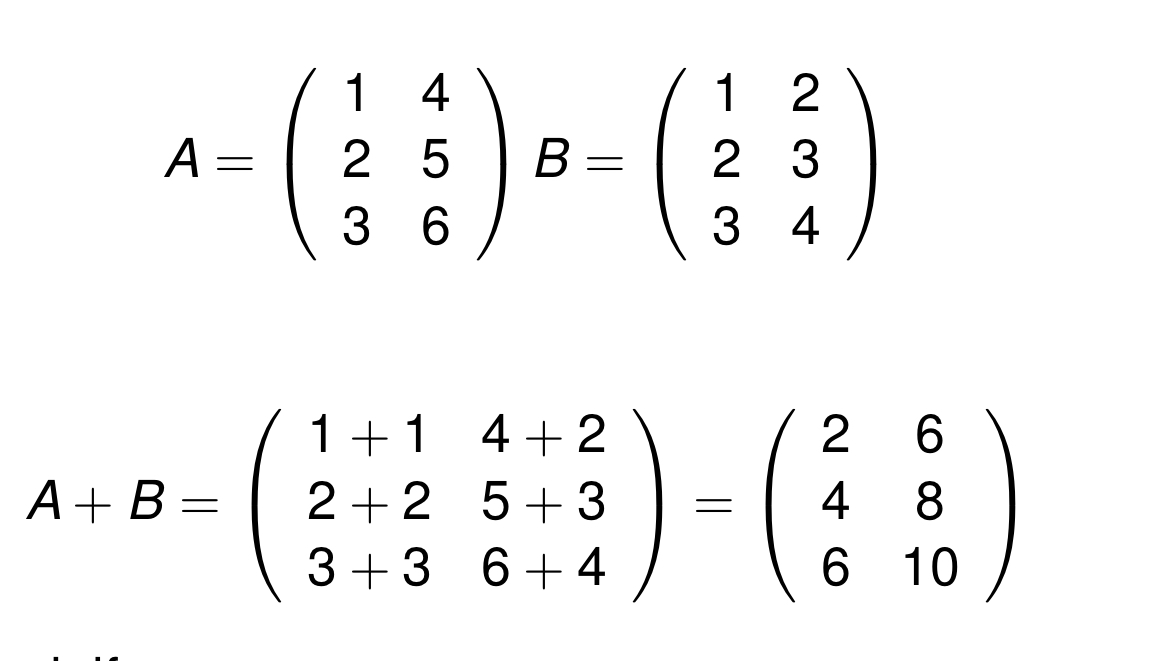
그렇다면 이제 식을 표현해보자.

$Y_i = E(Y_i)+\mathit{\epsilon}_i$
이를 헹렬로 표현하면 $Y = E(Y) +\mathit{\epsilon}$ 이 된다.

Multiplication of a matrix

$A = (a_{ij})$ 이고 $k$ 가 scalar라면
$kA = Ak = (ka_{ij})$ 이다.

matrix 끼리의 곱

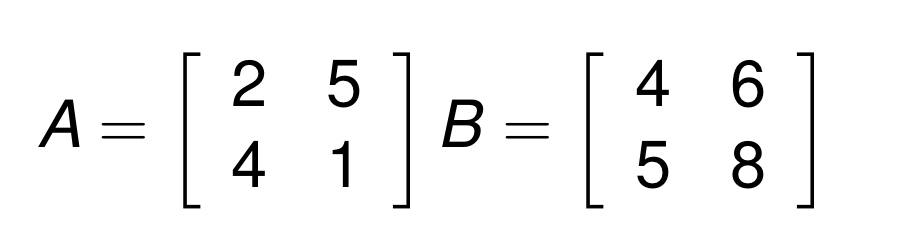
위와 같은 행렬이 있을 때, 우리는 A의 첫번째 행과 B의 첫번째 열을 cross product한 값을 곱의 첫 원소로 적어준다.
이런 방식으로 계산을 해나가면 된다!

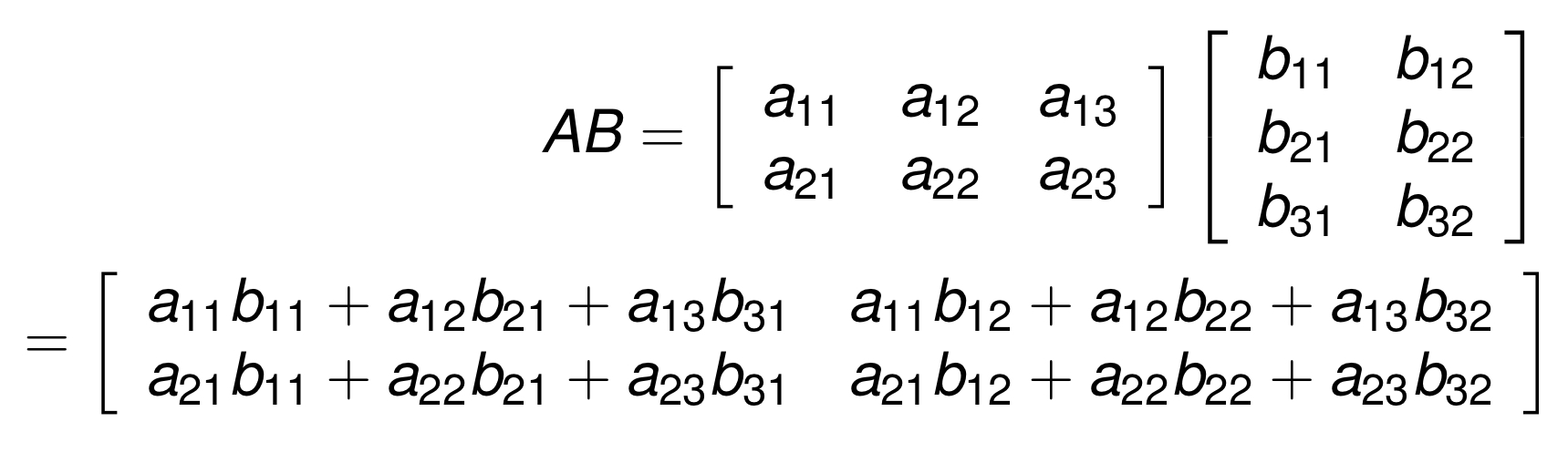
이러한 이유로 행렬을 곱계산할때는 반드시 숫자가 매치되어야한다.

이를 regression example로 살펴보면 다음과 같다.

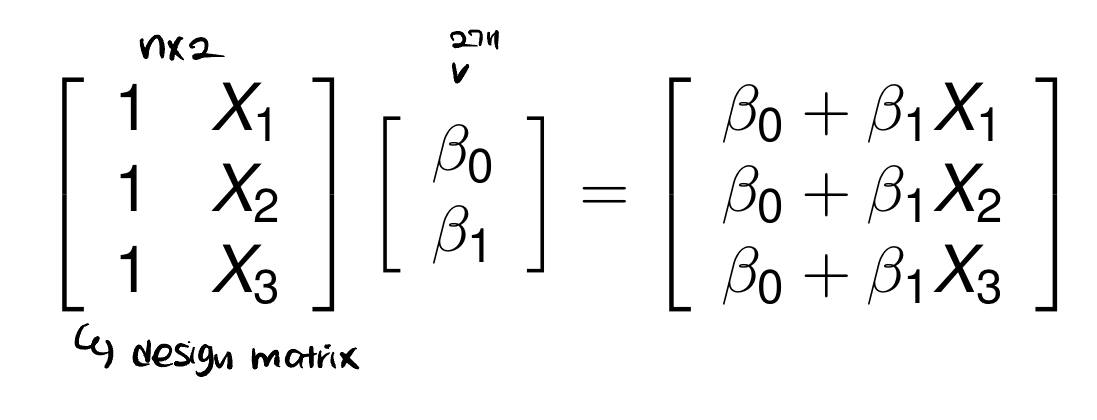
앞의 Matrix는 design matrix이고 뒤에는 우리가 추정할 계수이다.

더 중요한 부분은 내일 다루겠다..!