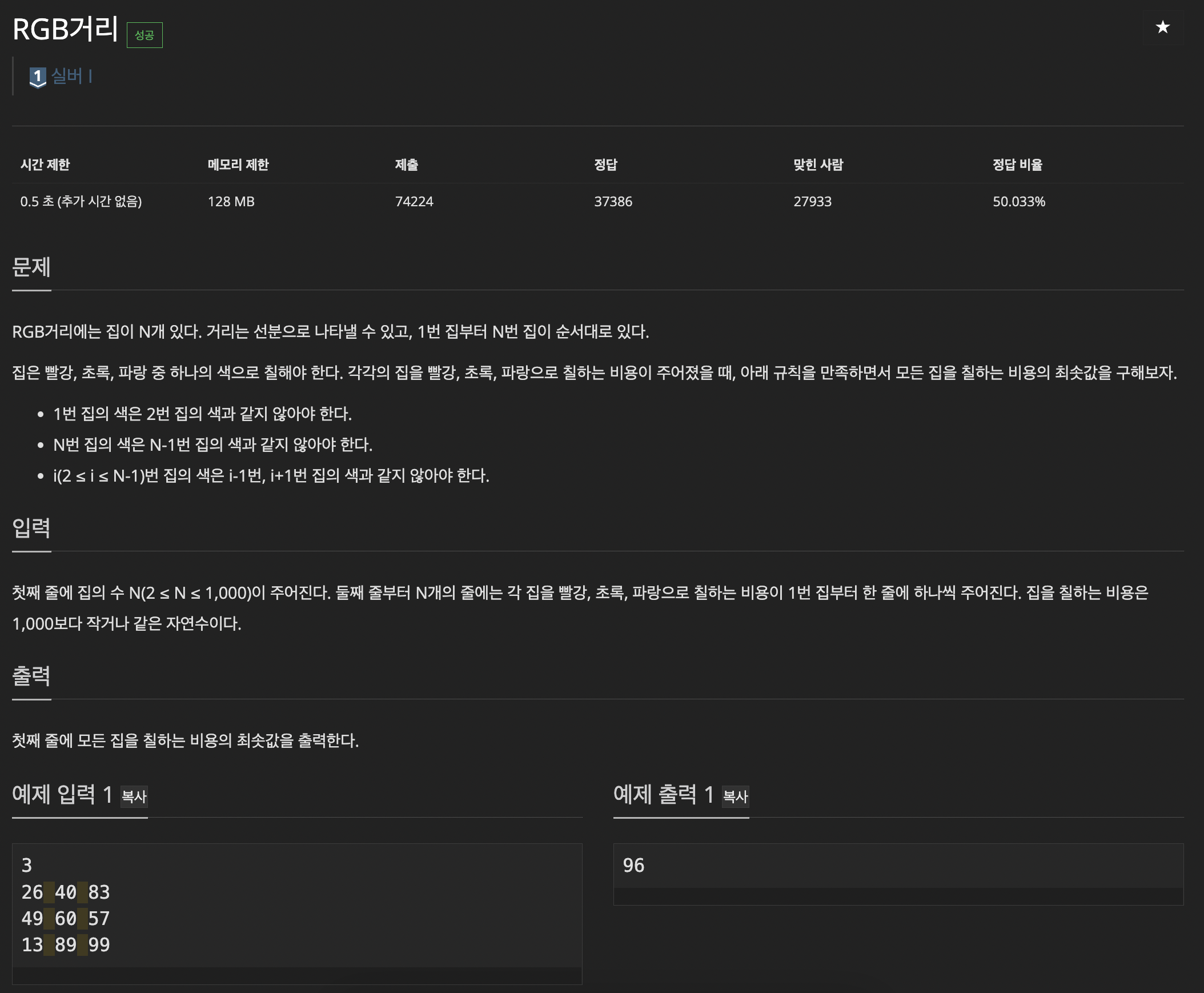
https://www.acmicpc.net/problem/1149
1. 아이디어
[i]번째 집
=>[i-1],[i+1]번째 집의 색과 달라야 함1번 ~n번 집까지 색을 칠해나갈 때,
[i]번 집은 이전[i-1]번 집의 색과 다른 2가지 색 중에서 선택
=> 차례대로 각 집에 대해, 3가지 색을 칠했을 때의 최소 합을 저장해나감
1) DP 배열 정의
-
int[][] dp = new int[n + 1][3] -
행: 집 번호, 열:
[0 ~ 2]차례로 RGB -
dp[i][j]:[i]번 집에[j]에 해당하는 색을 칠할 때,
[1]~[i]번 집까지의 색칠 최소 비용 합
=> 마지막 집까지 색칠했을 때, 최소 비용 합 = DP 행렬의 마지막 행에서 최소 값
2) 규칙 및 점화식
① [i]번 집을 R 색으로 칠하는 경우의 최소 비용 합
- min(
[i-1]번 집을 G 색칠하는 경우의 최소 비용 합,
[i-1]번 집을 B 색칠하는 경우의 최소 비용 합
)
+[i]번 집을 R 색칠하는 비용
=> dp[i][0] = min(dp[i-1][1], dp[i-1][2]) + cost[i][0]
② [i]번 집을 G 색으로 칠하는 경우의 최소 비용 합
- min(
[i-1]번 집을 R 색칠하는 경우의 최소 비용 합,
[i-1]번 집을 B 색칠하는 경우의 최소 비용 합
)
+[i]번 집을 G 색칠하는 비용
=> dp[i][1] = min(dp[i-1][0], dp[i-1][2]) + cost[i][1]
③ [i]번 집을 B 색으로 칠하는 경우의 최소 비용 합
- min(
[i-1]번 집을 R 색칠하는 경우의 최소 비용 합,
[i-1]번 집을 G 색칠하는 경우의 최소 비용 합
)
+[i]번 집을 B 색칠하는 비용
=> dp[i][2] = min(dp[i-1][0], dp[i-1][1]) + cost[i][2]
2. 자료구조
int[][] dp
=> 마지막 행의 최대값: 10^3 x n
=> n 최대값 대입: 10^3 x 10^3 = 10^6 << 21억 이므로,int가능
3. 시간 복잡도
- 2중 for 문 n x 3 만큼 반복: O(3n)
=> n 최대값 대입: 3 x 10^3 << 0.5억
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int n; // 집 개수
static int[][] cost; // 각 집의 R, G, B 색칠 비용
static int minSum = Integer.MAX_VALUE; // 출력, 최소 비용 합
static int[][] dp; // 각 집의 R, G, B 색칠 비용 최소 합
static void solution() {
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 3; j++) {
// [i]번 집을 R 색으로 칠하는 경우의 최소 비용 합
dp[i][0] = Math.min(dp[i-1][1], dp[i-1][2]) + cost[i][0];
// [i]번 집을 G 색으로 칠하는 경우의 최소 비용 합
dp[i][1] = Math.min(dp[i-1][0], dp[i-1][2]) + cost[i][1];
// [i]번 집을 B 색으로 칠하는 경우의 최소 비용 합
dp[i][2] = Math.min(dp[i-1][0], dp[i-1][1]) + cost[i][2];
}
}
// 마지막 행에서 minSum 찾기
for (int j = 0; j < 3; j++) {
if (minSum > dp[n][j])
minSum = dp[n][j];
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(
new InputStreamReader(System.in)
);
StringTokenizer st;
n = Integer.parseInt(br.readLine());
cost = new int[n + 1][3]; // [1][0] ~ [n][2] 사용
dp = new int[n + 1][3]; // [0]행에 패딩
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < 3; j++)
cost[i][j] = Integer.parseInt(st.nextToken());
}
solution();
System.out.println(minSum);
}
}