백준 12865, 평범한 배낭 - DP (a.k.a 0-1 Knapsack Problem)

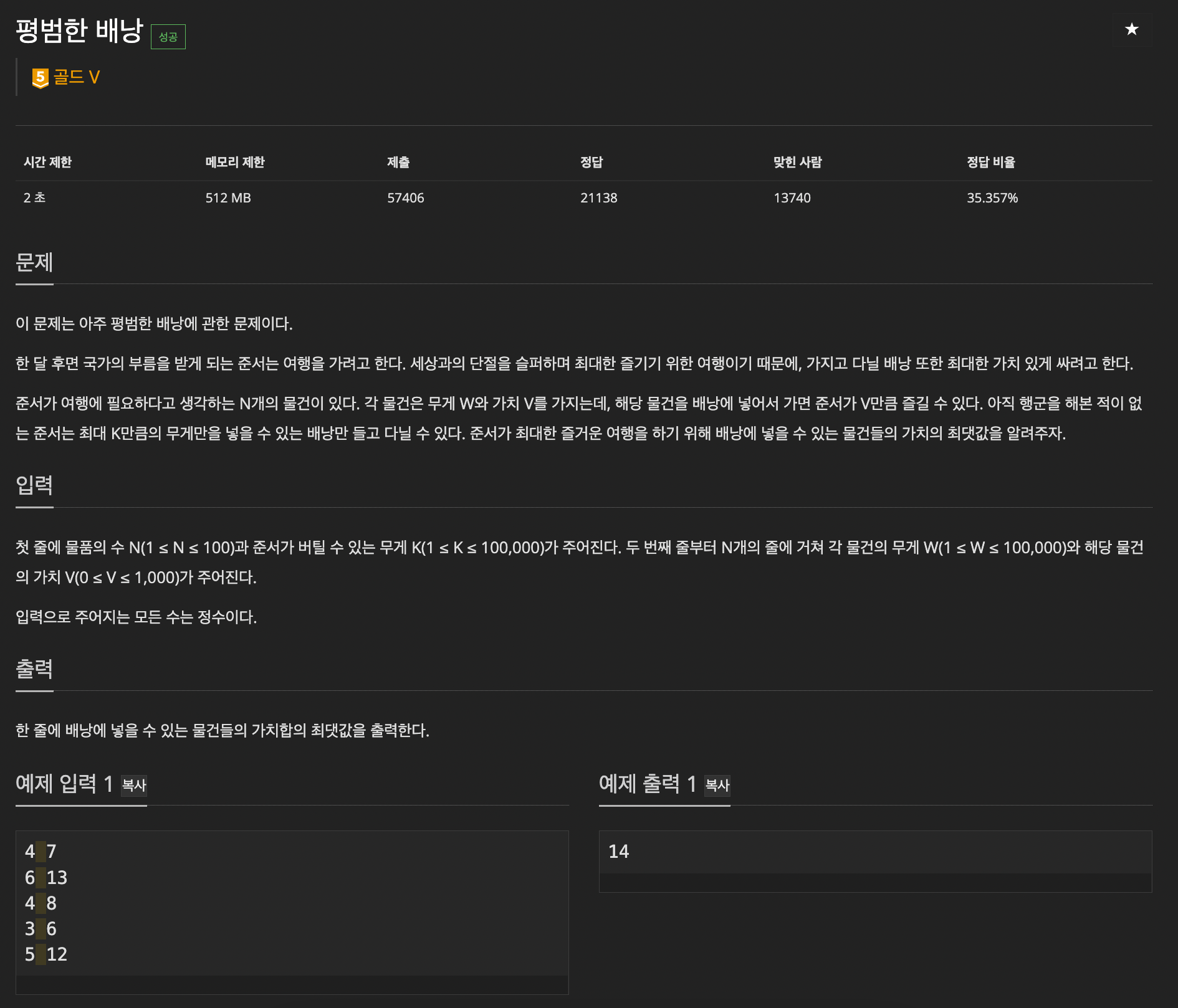
https://www.acmicpc.net/problem/12865

1. 아이디어

0-1 Knapsack Problem

• Item 을 쪼갤 수 없으므로, DP 로 풀이
  
  <=> Item 을 쪼갤 수 있는 Fractional Knapsack Problem 은 Greedy 로 풀이

---

1) DP 배열 정의: int[][] dp

• dp[i][j]: 첫 번째 ~ [i]번째 물건까지에서, 가방의 무게 용량이 j일 때의 최대 가치 합

2) 규칙 및 점화식

[i]번째 물건을 넣었을 때 or 넣지 않았을 때, 둘 중에서 가치 합이 더 큰 경우를 선택


① [i]번째 물건을 담을 수 없는 경우 ([i]번째 물건의 무게 w[i] > 가방 무게 용량 j)

• [i]번째 물건을 제외한, 나머지 [i-1]번째 까지의 물건들로 최대 가치 합 구성
  => dp[i][j] = dp[i - 1][j]
  
  

② [i]번째 물건을 담을 수 있는 경우

• ([i]번째 물건을 담기 위해 [i]번째 물건의 무게 만큼을 빼주고,
  [i-1]번째 까지의 물건들로 최대 가치 합 + [i]번째 물건의 가치)
  or
  ([i-1]번째 까지의 물건들로 최대 가치 합)
  => 2가지 중에서, 가치 합이 더 큰 것 선택
  => dp[i][j] = max(dp[i - 1][j - w[i]] + v[i], dp[i - 1][j])
  
  

구하는 답 = dp[n][k]
=> [n]번째 까지의 물건으로 최대 무게 k를 넘지 않을 때, 최대 가치 합

2. 자료구조

• int[][] dp
  ① 자료형: 최대 가치 합 100 x 10^5 = 10^7 << 21억 이므로, int 가능
  ② 메모리: 최대 4 x 100 (물건 개수 n) x 10^5 (가방 최대 무게 용량) byte
  = 4 x 10^7 byte = 40 MB << 512 MB 이므로, 가능

3. 시간 복잡도

• 2중 for 문: O(n x k)
  => n, k 최대값 대입: 100 x 10^5 = 10^7 << 2억

코드

import java.io.*;
import java.util.StringTokenizer;

public class Main {
	static int n, k;				// 물품의 수 n, 최대 무게 합 k
	static int[] w;					// 각 물건의 무게 w
	static int[] v;					// 각 물건의 가치 v
	static int maxValueSum;			// 물건들의 최대 가치 합
	static int[][] dp;

	static void solution() {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= k; j++) {
				if (w[i] > j)		// 물건을 담을 수 없는 경우
					dp[i][j] = dp[i - 1][j];
				else				// 물건을 담을 수 있는 경우
					dp[i][j] = Math.max(
							dp[i - 1][j - w[i]] + v[i],
							dp[i - 1][j]
					);
			}
		}

		maxValueSum = dp[n][k];
	}

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(
				new InputStreamReader(System.in)
		);
		StringTokenizer st = new StringTokenizer(br.readLine());

		n = Integer.parseInt(st.nextToken());
		k = Integer.parseInt(st.nextToken());

		w = new int[n + 1];			// [1] ~ [n] 사용
		v = new int[n + 1];
		for (int i = 1; i <= n; i++) {
			st = new StringTokenizer(br.readLine());
			int weight = Integer.parseInt(st.nextToken());
			int value = Integer.parseInt(st.nextToken());

			w[i] = weight;
			v[i] = value;
		}

		dp = new int[n + 1][k + 1];		// [0][0] ~ [n][k] 사용, [0]행과 [0]열은 패딩
		solution();
		System.out.println(maxValueSum);
	}
}