Intro.

고객이 보낸 과일 사진을 구별하는 '군집' 작업을 했었다. '샘플 평균값'을 활용해 대표 이미지(ex.apple_mean)를 얻은 뒤, 그것과 개별 사진들의 차이를 바탕으로 과일을 구분할 수 있었다! 하지만, 타깃을 알고 있었으니 사실상 '비지도 학습'이 아니었다...
➡️ 전달받은 이미지 300개가 사과 몇 개 파인애플 몇 개 바나나 몇 개인지 아무것도 모르는 상태에서, 위와 같은 대표 이미지(=평균값)을 구할 수 있을까?

1. k-평균 알고리즘

아무것도 모르는 사진 300장을 받았을 때, 위에서 말한 '평균값'을 자동으로 찾아주는 알고리즘이 있다?!?

k-평균 알고리즘의 작동 방식

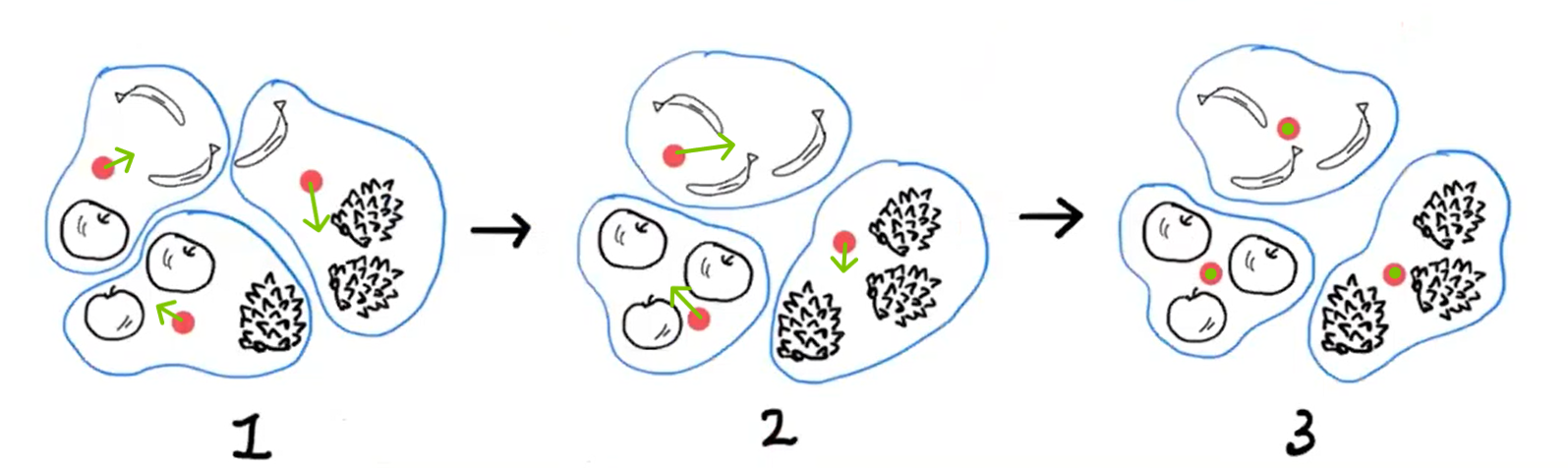
1. 무작위로 k개의 '클러스터 중심'을 정한다.
   • 이때, '클러스터 중심'이란 296p의 apple_mean 같은 '평균값(대표이미지를 구성하는 픽셀 10,000개)'을 다르게 표현한 것뿐임.
2. 지정한 클러스터 중심에서 가장 가까운 샘플들을 하나의 클러스터로 묶는다.
   • 이때, 가장 가까운 '몇 개'를 할지를 n_clusters로 설정함. (*뒤에 나옴)
3. 이제, 묶여있는 클러스터 내의 샘플들로, 새롭게 '클러스터 중심(평균값)'을 계산한다.
   • 이렇게 계산하면, 당연히 처음과 다른 k개의 평균값이 구해짐.
     = 클러스터 중심이 이동했다고 표현하는 것과 같은 말임.
4. 그 달라진 '클러스터 중심'에서 가장 가까운 샘플들을 다시 묶는다.
   • '클러스터 중심'이 달라졌으니, 당연히 거기서 가까운 샘플들도 달라졌을 것임. 이전의 클러스터는 버리고, 그 중심으로 새로운 클러스터를 만든다고 보면 됨.
5. 클러스터 중심에 변화가 없을 때까지 이 과정을 반복한다.
   • 새로운 클러스터를 만들고(4), 다시 그 구성원(샘플)들로 클러스터 중심을 계산하고(다시 3), 그 클러스터 중심으로 다시 새로운 클러스터를 만들고(다시 4), ••• 하다보면,
     결국 비슷한 애들끼리 모인 곳의 중심에 '클러스터 중심'이 잡히게 될 거임!

2. KMeans 클래스

사이킷런의 k-평균 모델로 과일을 알아서 구분하는 비지도학습 모델을 만들어보자!

모델 훈련하기

• 300개의 과일 데이터 준비하고 넘파이 배열로 불러옴
  
• (샘플개수, 너비, 높이) 크기의 3차원 배열을 (샘플개수, 너비*높이) 크기의 2차원 배열로!
  
• 언제나 그랬듯 .fit()으로 모델 훈련 (단, 비지도학습이니 입력데이터만 넣어줌!)
  KMeans() : 사이킷런에서 k-평균 알고리즘이 구현되어있는 클래스
  n_clusters : 클러스터 개수를 지정하는 매개변수 (*)
  
• 군집(clustering)의 결과는 .labels_에 저장되어 있음. (0,1,2 순서 같은 건 의미 없음)
  
• 각 레이블에 몇 개씩 묶였는지 확인해보고 싶으면 np.unique()를 활용!
  return_counts : 고유값의 개수를 보여주는 옵션 매개변수
  

그림으로 그려서 확인하기

• 클러스터에 들어있는 이미지를 그려주는 함수를 직접 만듦.
  draw_fruits : arr에 3차원 배열을 입력받아서 그림으로 출력해줄 함수.
  squeeze=False : axs를 항상 2차원 배열로 다루기 위해서 설정해줌.
  
• 이렇게 만든 함수를 사용해서, 각 클러스터(0/1/2)에 속한 샘플들을 그려보자.
  (feat. 불리언 인덱싱)
  레이블 0에는 파인애플 / 레이블 1에는 바나나 / 레이블 2에는 사과로,
  타깃 없이도 알아서 꽤나 잘 모았네! (0에는 섞인 거 약간 있지만..!)

클러스터 중심을 활용하기

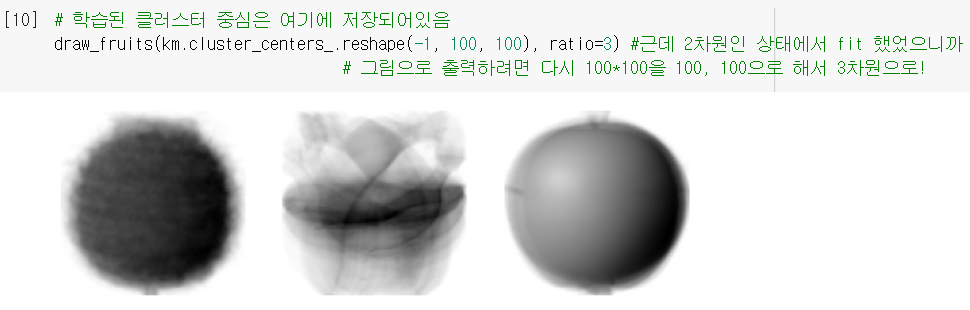
• 위에서 KMeans 모델이 fit으로 찾았던 '클러스터 중심(=샘플 평균값)'은 .cluster_centers_에 저장되어 있음.
• 그걸 3차원 배열로 다시 바꿔서 그림으로 확인해보니, 이전 시간에 본 것과 동일한 '평균 이미지(대표 이미지)'가 나옴!
  
• KMeans의 또 하나 유용한 기능은 바로 .transform() 메소드인데, 특정 샘플을 집어넣으면, 그 샘플과 클러스터 중심들까지의 거리로 반환해 줌.
  ❗ 10000개(픽셀)의 특성을 3개(거리)의 특성으로, 차원을 줄여주는 변환기로 사용 가능!
  
• 이 거리를 이용해 예측 클래스를 출력해주는 .predict() 메소드도 제공함.
  ↪ '이 경우엔 첫 번째 클러스터까지의 거리가 가장 작으니까 레이블 0에 속할 것 같네' 라고 생각했는데, predict로 출력해보니 정말 그러함!
  
• 그림까지 그려서 확인사살해보면, 레이블 0에 있던 파인애플이 맞음!
  .n_iter_ : 클러스터 중심을 옮기는 '반복 횟수'가 저장된 속성
  
  ➕참고로, .transform()과 .predict()는 다른 군집 알고리즘엔 잘 없음. KMeans의 특징적인 메소드임...!

3. 최적의 k 찾기

k-평균 알고리즘의 단점

• 우린 지금 사과/파인애플/배 3종류인 거 알아서 n_cluster=3 으로 fit 했었음.
  근데 그걸 모르는 상태에선, 클러스터 개수를 몇 개로 할 지 판단하기 쉽지 않음...
• 적절한 k값을 찾기 위한 완벽한 방법은 없지만, 몇 가지 보완 방법이 있음.

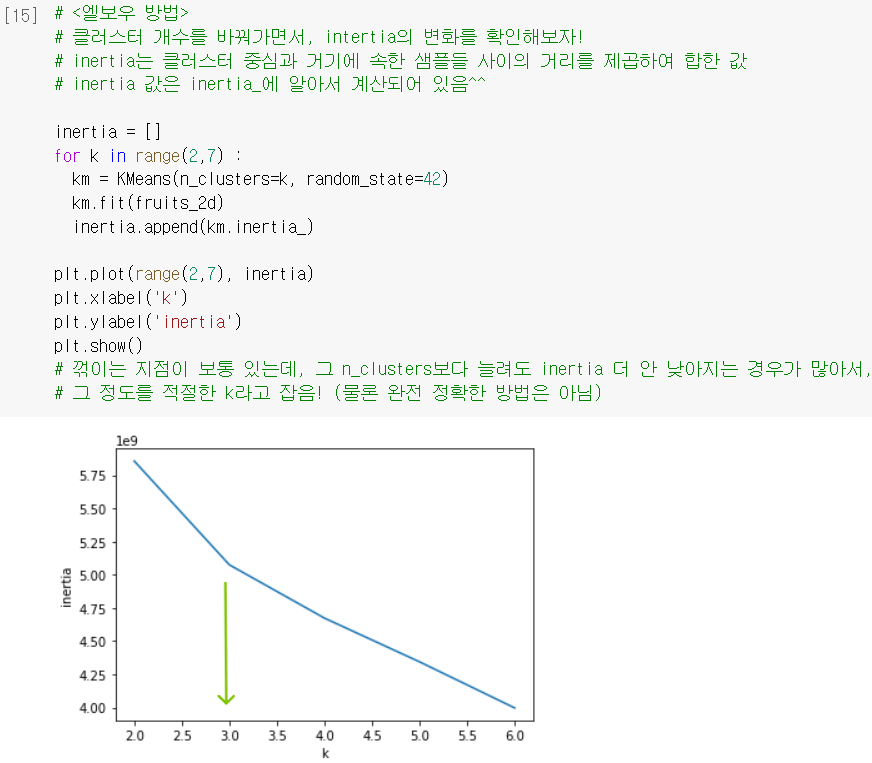
엘보우(elbow) 방법

1) 앞에서 .transform()으로 구했던 '거리'의 제곱 합을 이너셔(inertia)라고 함.
2) 이 이너셔 값이 작다는 것은, 클러스터 중심에 샘플들이 조밀하게 잘 모여있다고 해석할 수 있음. (= 작을수록 좋다고 볼 수 있음)
3) 보통 클러스터 개수(k)를 늘리면, 더 곳곳에 센트로이드가 자리하니까 이너셔가 줄어듦.

• 이 원리를 활용해, 클러스터 개수를 바꿔가면서 이너셔 값의 변화를 그래프로 살펴보면,
  보통 감소 속도가 꺾이는 지점이 있기 마련 ➡️ 그 지점을 최적의 k로 채택!
  .inertia_ : KMeans에서 자동으로 계산한 이너셔 값
  하지만 이 방법도 명확하진 않기 때문에, 다른 지도학습이나 문제에 적용하면서 후속작업을 진행하고, 그 결과를 바탕으로 feedback하면서 모델을 개선하는 경우가 많음.

➕플러스 알파

➊ KMeans에 적합한 데이터

• k-평균 알고리즘은 클러스터 중심에 대한 직선거리를 이용하기 때문에, 원형에 가까운 클러스터에 적합함. (아래처럼 타원형으로 묶이는 경우는 잘 못 찾음)
• 즉, 특성간 거리가 비슷한 스케일 내의 값들이어야 KMeans가 잘 분석할 수 있음.
  → ∴ 표준화 등으로 스케일 전처리를 해주고 쓰는 것이 좋음.
• 우리가 다룬 사진 데이터의 경우는, 픽셀값들이 0~255 사이에 안정적으로 정의되어 있어서 따로 전처리해주지 않아도 됐었던 거임.
  

---

🤔 Hmmmm...

307p. draw_fruits 함수 내에서 n=len(arr)로 정의하는데, arr에 3차원 데이터를 집어넣어도 len, 즉 '길이'라는 걸 계산할 수가 있는 건가요? 그냥 알아서 1차원으로 펼쳐서 개수를 세는 걸까요..?

👨🏻‍🏫 len() 함수는 첫 번째 차원의 길이를 반환합니다. 🆗

⭐310p. transform 함수를 사용할 때, fruits_2d[100] 으로 하는 것과 fruits[100:101]로 하는 것의 차이를 모르겠습니다ㅠㅠㅠ

fruits_2d[100]은 2차원 배열에서 101번째 원소(1차원 배열)를 선택합니다. 🆗
그러니까 이게, 그냥 [100]으로 '인덱싱'을 하게 되면 그냥 원소를 (1차원 크기로) 조회하게 되는 것인데, [100:101]로 '슬라이싱'을 하게 되면 2차원 배열을 형태가 유지된 채로 그 부분을 뽑아쓰는 거라고 보면 될 듯! 여기서 transform 함수는 2차원 배열을 기대하니까 후자를 사용해야 하는 거고!
※ 그냥 [100]으로 출력해봐도 겉에 [ ]가 감싸져있어서 나는 그게 (1,10000) 크기의 리스트인 줄 알았다. 근데 그건 그냥 numpy array view 라고 한다 ..

🤓 To wrap up...

이번엔 정말로 '타깃'이 없는 상황에서, 알아서 자기가 어떤 패턴을 학습하는 알고리즘을 배웠다. 수학적인 논리를 기반으로 알아서 학습하는 모델을 만든다는 게 새삼 신기했고, AI가 어떤 느낌인지 좀 더 가까이서 보게 된 느낌이다. 머신러닝만으로 할 수 있는 프로젝트를 하루빨리 찾아야한다! (* [11]에 나온 슬라이싱 문법 하나 때문에 애를 엄청나게 먹었다... 기본기를 더 다져야한다....)

타깃 모르는 상태에서 (제대로 된 비지도학습) 사진을 분류하기 위해 k-평균 알고리즘 도입 → 사이킷런의 KMeans 클래스를 사용하여 clustering → 군집 결과는 labels_에, 계산된 '클러스터 중심'은 cluster_centers_에 저장됨 → 결과를 이미지로 그려보니, 알아서 비슷한 것끼리 잘 묶었음!👏🏻 → transform() 메소드를 사용하면 특정 샘플을 거리로 변환하여, 데이터의 차원을 줄일 수 있음 & predict() 메소드도 제공함 → 하지만 KMeans는 결정적으로, 적절한 클러스터 개수를 사전에 지정해야 한다는 단점이 있음 → 이를 해결하기 위한 한 가지 방법으로, inertia_를 활용한 엘보우 방법을 사용해 봄.