Intro.

🚨고객들이 보낸 과일 사진이 너무 많아지면서, 저장공간이 부족해졌다... 업로드된 사진의 용량을 좀 압축시킬 수는 없을까?

1. 차원 축소

'차원'이라는 용어

• 지금까지 우리는 데이터가 가진 속성을 '특성'이라고 불렀음. (ex. 과일 사진의 각 샘플은 10,000개의 특성으로 이루어짐) 머신러닝에선 이 '특성'을 '차원'이라고도 부름.

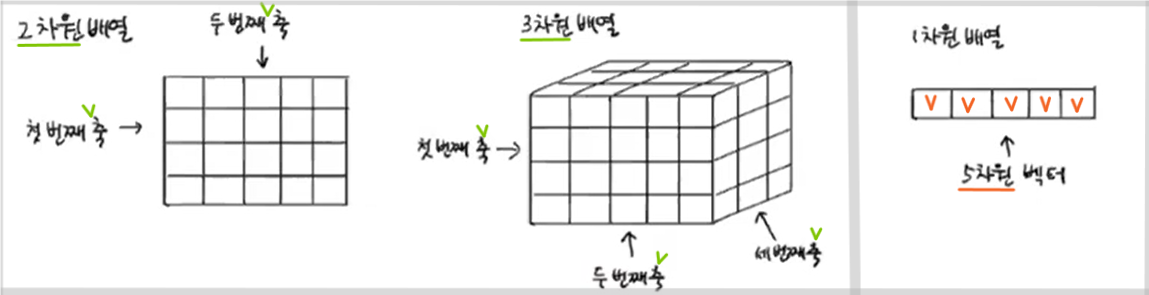
⭐다차원 배열과 1차원 배열에서 용어가 다르게 쓰임.

• 다차원 배열 : 차원 = 축의 개수 / 1차원 배열(벡터) : 차원 = 원소의 개수
• ❗지금 '차원 축소'에서 축소한다는 차원은 후자❗ (벡터로서의 차원)

차원 축소

• 비지도학습의 한 종류로, 데이터를 가장 잘 나타내는 일부 특성을 선택하여
  데이터 크기를 줄이고 다른 알고리즘의 성능을 향상시킬 수 있는 방법
  • 특성 개수가 많아지면 과대적합되는데, 이를 막아줌
  • 특성 개수가 줄어드니까 당연히 용량도 줄여줌.
  • 시각화하기도 쉬워짐.
• 반대로, 줄어든 차원에서 원본 차원으로 복원할 수도 있음.
• 대표적으로 주성분 분석(Principal Component Analysis)이 있음.

2. 주성분 분석

1st 주성분

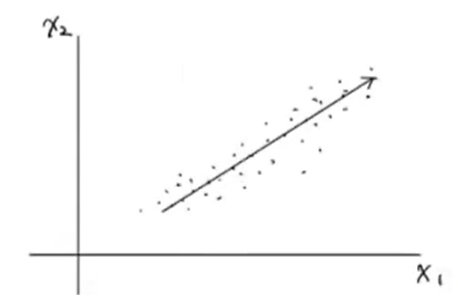
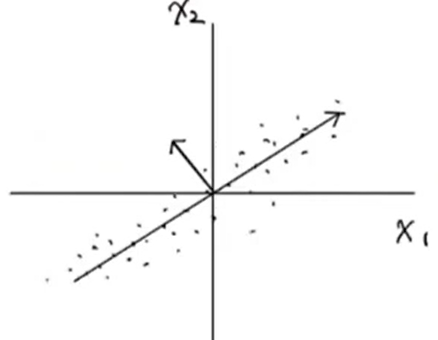
• 데이터에서 분산이 가장 큰 방향을 찾아보면 대략 아래처럼 그릴 수 있음.
  ( =가장 많이 퍼져있는 방향 = 데이터를 가장 잘 표현하는 방향 )
  
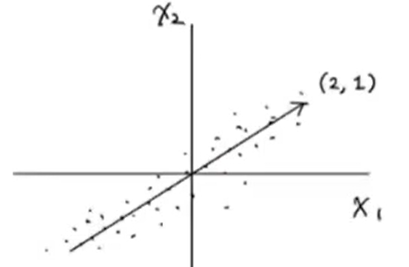
• 이 직선을 원점으로 옮기면 벡터로 표현하기 쉬워지고, 이 벡터 (2,1)이 주성분이 됨!
  = 특성은 X1, X2 로 2개였는데 ➡️ (2,1) 이라는 1개의 데이터로 표현가능해졌음!!
  ❗참고로, 사이킷런의 PCA 모델은 알아서 특성을 원점에 맞춰주니까 우리가 수동으로 할 필요 없음
  
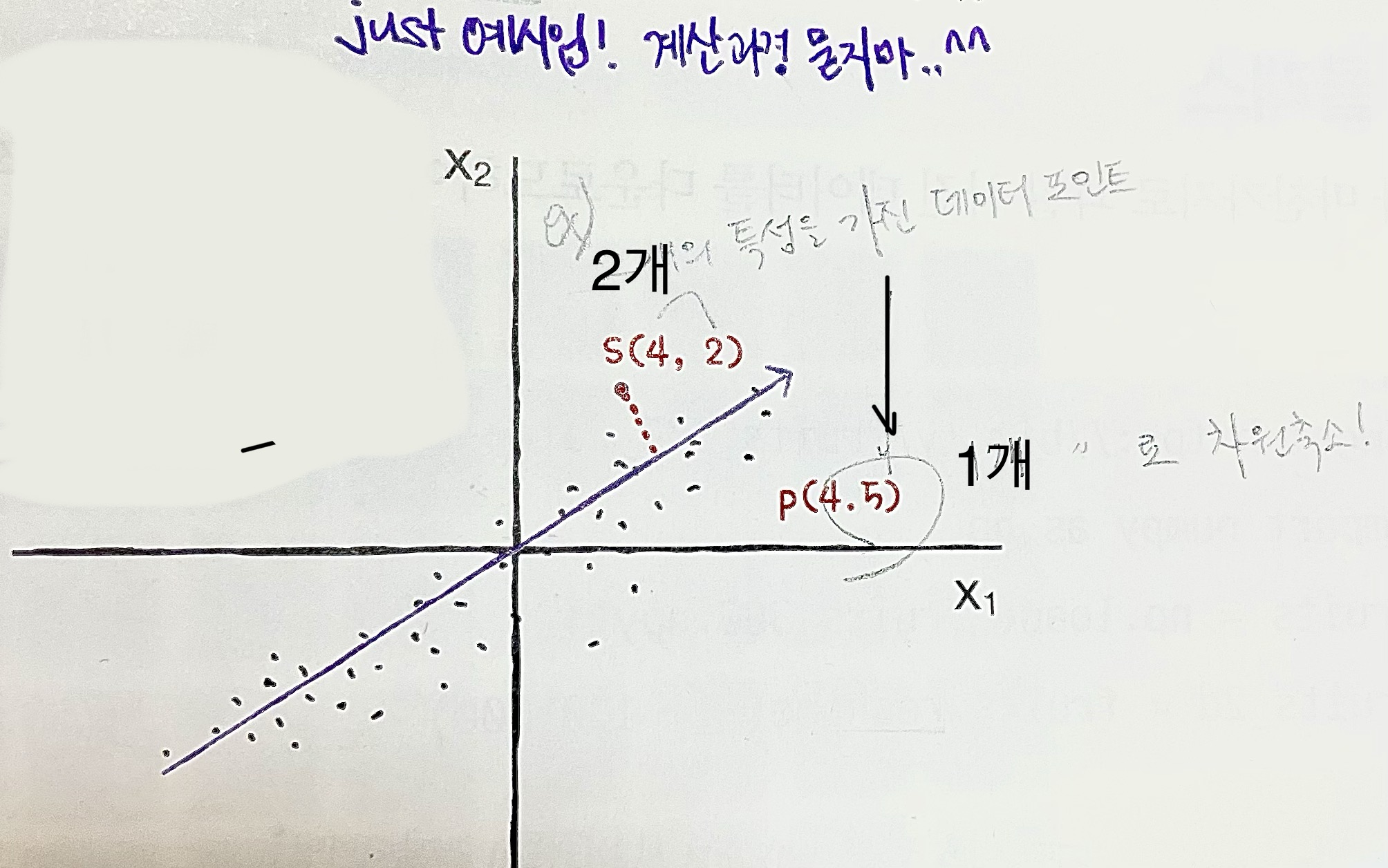
• 이 주성분(벡터)을 활용하면, 원본데이터의 차원을 줄일 수 있음. 예를 들면,
  아래처럼 (4,2)라는 2차원 샘플을 "주성분에 투영하면" 1차원 데이터 (4.5)로 만듦.
  

2nd 주성분

• 주성분은 1개로 끝나는 게 아니라 더 찾을 수 있음. = 원본의 특성 개수만큼 찾을 수 있음
  (ex. 지금은 X1, X2로 2차원이니까, 주성분 최대 2개까지 찾을 수 있음)
• 첫 번째 주성분에 수직이면서, 분산이 가장 큰 다음 방향을 찾으면 됨.
  = 1st 주성분이 표현하지 못하는 분산의 방향을 찾는 게 효율적이니까!
  
  근데 사실, 원본 특성이 2개인데 주성분 2개를 다 찾으면 차원축소가 안 되는 셈이니, 보통은 더 적은 개수의 주성분만 찾아서 활용합니다..!

3. PCA 클래스

주성분의 특징을 배웠으니, 이제 사이킷런에서 진짜 주성분 분석을 수행해보자!

주성분 분석

• 동일하게 300장의 과일 사진 데이터 준비.
  
• 이번에도 비지도학습이니까, .fit()에 입력데이터만 전달해서 모델 훈련.
  PCA() : 사이킷런에서 주성분 분석 알고리즘이 구현되어있는 클래스
  n_components : 찾을 주성분의 개수를 지정하는 매개변수
  
• 뽑아낸 주성분(pca)은 .components_에 저장되어 있음.
  ❗321p에선 2개의 특성이 있는 원본공간을 가로지르는 주성분을 찾았다면, 이번엔 10000개의 특성이 있는 원본공간을 가로지르는 주성분을 찾았다고 보면 됨
  
• 찾은 주성분을 이미지로 출력해보니, (이전에 썼던 draw_fruits 함수 그대로 사용)
  마치 원본 데이터셋의 어떤 패턴을 잡아낸 것처럼 보임!
  
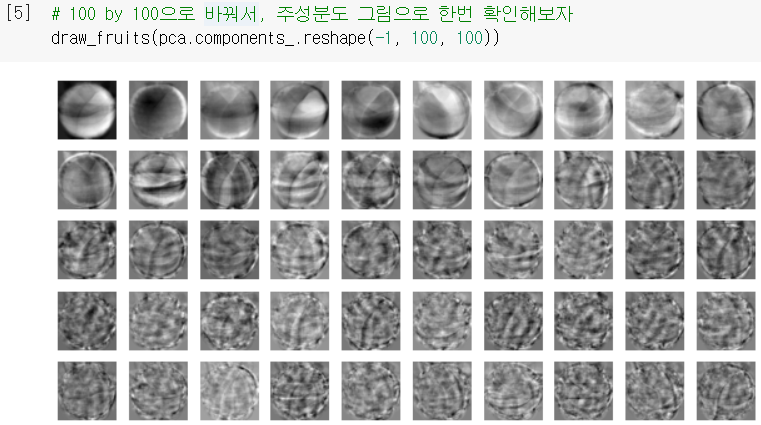
• 주성분을 찾았으니, 이제 데이터를 주성분에 투영하여 차원(특성 개수)을 줄일 수 있음!
  ⭐.transform() : 전달받은 데이터를 주성분으로 분해(차원 축소)하는 메소드
  원래 (300,10000) 크기의 배열을 (300,50)으로 변환하니, 무려 $1/200$로 용량이 줄어든 셈!

원본 데이터 재구성

• 앞에선 특성 개수를 줄였다면(10000→50), 반대로 원본 데이터를 복원(50→10000)할 수도 있음.
  (압축할 때 손실이 있었으니 100% 그대로는 당연히 안 됨)
  .inverse_transform() : 주성분을 바탕으로 원본 데이터를 재구성해주는 메소드
  
• 이번에도 그림으로 출력해보니, 거의 모든 과일이 잘 복원됨! (고작 50개로 10000개를 재구성했는데 이정도면 very nice! 일부 흐리거나 번진 부분은 압축할 때 손실된 부분 ㅇㅇ.)
  대단해.. 대체 우리가 찾은 50개의 주성분이 원본의 분산을 '얼마나' 잘 나타내는 거길래?
  

설명된 분산

• 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값을 설명된 분산(explained variance)이라고 함.

• .explained_variance_ratio_ : 각 주성분의 설명된 분산 비율이 저장되어 있음.
  → 이 값을 sum으로 다 더하면 주성분 50개가 설명하는 총 분산 비율을 얻을 수 있음.
  ↪ 92%나 되는 높은 비율이네 ㄷㄷ.. 어쩐지 복원 너무 잘 하더라..!

• 설명된 분산 비율을 그래프로 그려보면, 적절한 주성분 개수를 찾는 데도 도움됨!
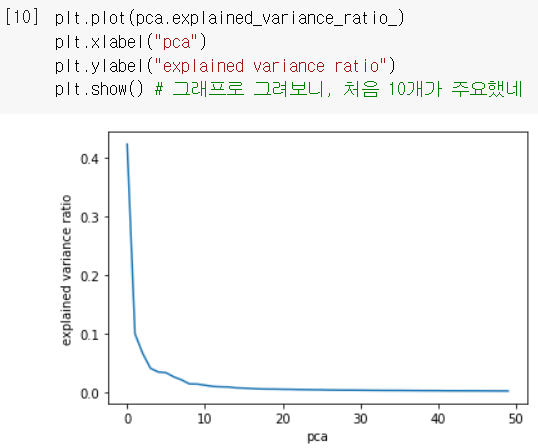  ↪ 당연히, 첫 번째 주성분이 가장 많이 설명함 ㅇㅇ
  ↪ 첫 10개 정도의 주성분이 대부분의 분산을 표현했네. (그 뒤쪽은 있으나마나한 주성분들 ...^^)

4. 다른 알고리즘과 연계

사실 용량을 줄여야한다는 상황은 스토리텔링 때문에 집어넣은 거구요..^^ PCA는 주로 다른 알고리즘과 연계하여 많이 사용합니다!

분류 알고리즘 (로지스틱 회귀)

• 모델을 만들고 타깃값(사과 0/파인애플 1/바나나 2)을 설정해줌.
  
• 먼저, 그냥 원본 데이터로 훈련해서 검증해보면... (cross_validate로 한번에!)
  
• 다음으로, PCA 차원축소한 데이터로 똑같이 해보면...
  특성 50개만 쓰니까 (성능은 유지하면서) 훈련시간이 감소되어 좋네! ㅎㅎ

군집 알고리즘 (k-평균)

• 모델을 만들고, (비지도학습이니까) 타깃값 없이 훈련!
• 입력값은 ➕에서 만든 특성 2개짜리 fruits_pca 사용 → 특성 2개만 썼는데도 306p에서 원본으로 KMeans 했던 것과 거의 동일한 결과! (플러스알파 참조)
  
• 이미지로 출력해서 확인해봐도 역시 306p와 비슷한 결과!
  

데이터 시각화

• 데이터를 차원축소하면 얻을 수 있는 또 다른 장점은 바로 '시각화'
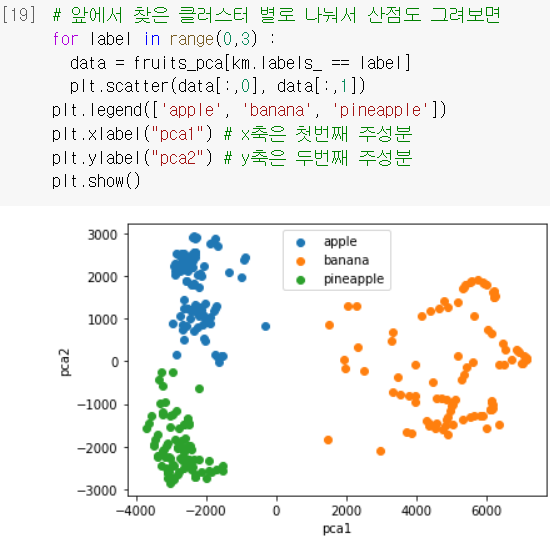
  = 10,000개의 차원은 지면에 그릴 수 없지만, 3개 이하로 차원을 줄이면 화면에 출력하기 쉬움!
• 특성 2개로 줄여놓은 fruits_pca를 클러스터 별로 산점도 그려보면 → 3개의 과일이 서로 구분 잘 되어 있음!! (=이래서 2개만 써도 로지스틱 회귀모델 성능 높았구나~)
  

➕플러스 알파

➊ n_components 설정

• PCA 모델을 만들 때, n_components 매개변수에 '찾을 주성분의 개수'를 지정하지 않고
  원하는 설명된 분산 비율을 입력해도 된다!
  ❗동일한 매개변수지만, 정수를 넣으면 '개수'로 인식하고 실수를 넣으면 '비율'로 알아서 인식한다.
• 원하는 비율에 도달하려면 몇 개의 주성분이 필요한지는 .n_components_에 저장된다!
  

---

🤔 Hmmmm...

320p. ‘주성분’이라는 게 데이터의 분산을 가장 잘 표현하는 방향을 찾는다고 하시니, 선형회귀의 회귀선으로 찾아도 되는 게 아닌가 하는 생각이 들었습니다. 회귀선을 사용하지 않고 굳이 ‘벡터’로 찾는 특별한 이유가 있는지 궁금합니다.

👨🏻‍🏫 주성분의 정의에 해당됩니다. 회귀가 분산이 큰 방향을 찾는 것은 아닙니다. ⏯️ 아 그치 회귀는 물론 '최소제곱법' 베이스인 건 아는데... 주성분이 어떻게 벡터를 활용해 정의될 수 있는지 보려면 많이 복잡하게 들어가야 하려나ㅠ

324p. inverse_transform 으로 복원할 때 원본데이터와 동일하게 10000개로 복원하셨는데, 실제로는 아예 똑같은 개수의 데이터로 복원하는 건 의미가 없지 않나요? 그냥 복원 과정 설명을 위한 예시라고 이해하면 되는거죠?

👨🏻‍🏫 원본 차원으로 복원하는 것이 필요한 작업이 있을 수 있지 않을까요? 🆗

324p. 그렇다면 inverse_transform을 사용할 때 원본과 다른 개수로 복원도 가능한지 궁금합니다. 이를테면 50개의 주성분을 바탕으로 5000개 정도만 샘플을 만들어보고 싶다거나 할 때 PCA를 사용할 수 있는 건가요?

👨🏻‍🏫 원본 차원보다 적은 차원으로 복원하는 것도 가능합니다. 🆗

325p. ❗for start in [0, 100, 200] 보고, 순간 range의 start, stop, step 인 줄 알았는데 아니었다..! 애초에 이렇게 리스트로 전달하면, 그 안에 있는 거 하나씩 start로 넣는 거였지.. 기억났다... 🆗

앞에서 배운 다른 알고리즘들과 달리, PCA는 어떤 문제해결에 직접적으로 쓰이기보다는 (마치 데이터 전처리처럼) 다른 모델을 사용하기 전에 차원을 축소해주는 변환기처럼 쓰이는 것이 주요 용도라고 이해해도 괜찮을까요?

👨🏻‍🏫 넵, 그렇게 생각하셔도 좋습니다. 🆗

😵‍💫 비슷해서 헷갈리는 녀석들 😵‍💫
n_components : PCA 모델 만들 때 설정하는 매개변수로, '개수' or '비율' 중 원하는 걸 입력하면 됨
.n_components_ : '비율'로 입력했을 때, 몇 개의 주성분이 필요한지가 저장되어 있음.
.components_ : (뭘로 하든 걍 결과적으로) 뽑아낸 주성분이 저장되어 있는 속성. 🆗

🤓 To wrap up...

벡터 개념을 제대로 몰라서 그런지 처음에 갈피를 잘 못 잡았다.. 주성분 분석 자체가 문제를 직접적으로 해결하는 (앞에서 배운) 알고리즘들과는 결이 다르다는 것을 인지하고 나니까 한결 이해가 편했다! (마지막 질문 참고) 선형대수학이 필요하겠다는 위기감이 스멀스멀... 벡터랑 행렬이라도 좀 봐놔야할 것 같다ㅠ

사진의 용량을 줄이기 위해 PCA 알고리즘 도입 → 특성 10,000개를 잘 설명하는 주성분 50개를 찾아냄 → 찾아낸 주성분 50개에 투영시켜, 원본데이터의 차원을 축소시킬 수 있음
(=특성 개수를 줄이니 용량이 절감됨) → 반대로 축소된 데이터를 원본 데이터로 복원할 수도 있었음 → 뽑아낸 주성분들이 원본 데이터를 얼마나 설명하는지도 구해볼 수 있음 → 다른 알고리즘과 연계하여 많이 활용되고, 시각화가 용이하다는 장점까지!
👏🏻[머신러닝 파트 끝]👏🏻