힙을 이용한 우선순위 큐

우선순위 큐 (priority queue) ?

• 스택 : 가장 최근에 들어온 데이터가 삭제되는 자료구조
  → 후입선출 (LIFO)
• 큐 : 가장 먼저 들어온 데이터가 삭제되는 자료구조
  → 선입선출 (FIFO)
• 우선순위 큐 : 가장 우선순위가 높은 데이터가 삭제되는 자료구조

우선순위 큐는 우선순위 개념을 큐에 도입한 자료구조이다.
우선순위를 가지고 있어 우선순위가 높은 데이터가 먼저 출력된다.
우선순위 큐는 삭제 연산에서 어떤 요소가 먼저 삭제되는가에 따라 두 가지로 나뉜다.

최대 우선순위 큐 : 우선순위가 가장 높은 요소 먼저 삭제
최소 우선순위 큐 : 우선순위가 가장 낮은 요소 먼저 삭제

우선순위 큐의 추상 자료형

• 데이터 : 우선순위를 가진 요소들의 모음
• 연산
  insert(item) : 우선순위 큐에 항목 item을 추가
  remove() : 우선순위 큐로부터 가장 우선순위가 높은 요소를 삭제하고 이를 반환
  find() : 우선순위가 가장 높은 요소를 삭제하지 않고 반환
  isEmpty() : 우선순위 큐가 공백 상태인지 검사
  isFull() : 우선순위 큐가 포화상태인지 검사
  display() : 우선순위 큐의 모든 요소들을 출력

우선순위 큐의 구현 방법

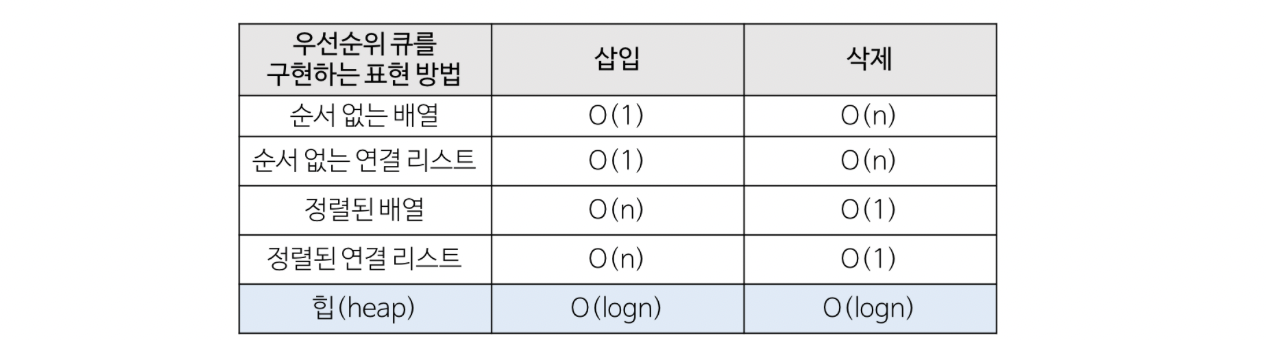
힙(heap) ?

• 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조
• 부모 노드의 키 값이 자식 노드의 키 값보다 큰 이진트리
• 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도의 느슨한 정렬 상태를 유지
• 힙의 목적 : 삭제 연산에서 가장 큰 값을 효율적으로 찾아내는것
  → 전체를 정렬할 이유 없음

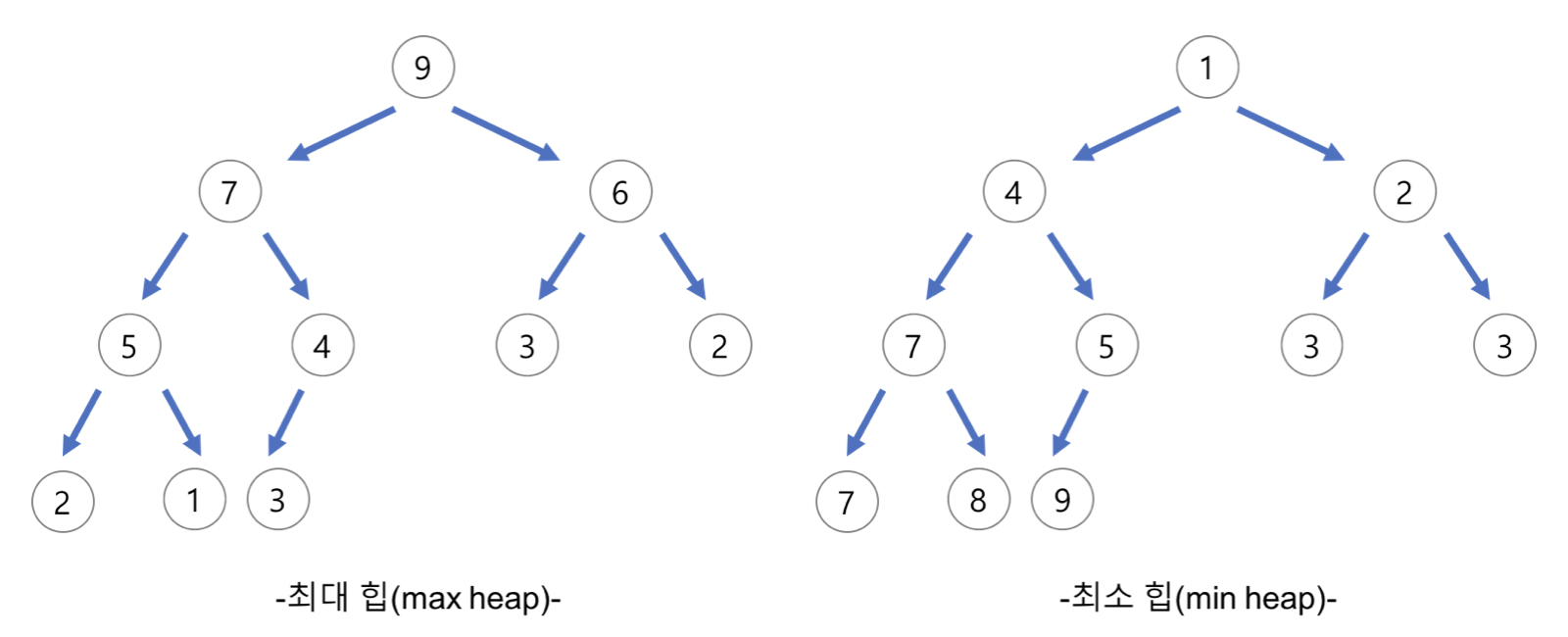
힙의 종류

최대 힙(max heap)

• 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리
• key(부모 노드 ) >= key(자식 노드)

최소 힙(min heap)

• 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진트리
• key(부모 노드 ) <= key(자식 노드)
  

힙의 구현 방법

힙은 완전 이진트리이기 때문에 중간에 비어있는 요소가 없다.
이 번호를 배열의 인덱스로 생각하면 배열에 힙의 노드들을 저장할 수 있다.
→ 힙을 저장하는 가장 효과적인 자료구조 : 배열
✔︎ 프로그램 구현을 쉽게 하기 위해 배열의 첫 인덱스인 0는 사용 ✘
✔︎ 트리의 모든 위치의 노드 번호는 새로운 노드가 추가되더라도 변하지 ✘

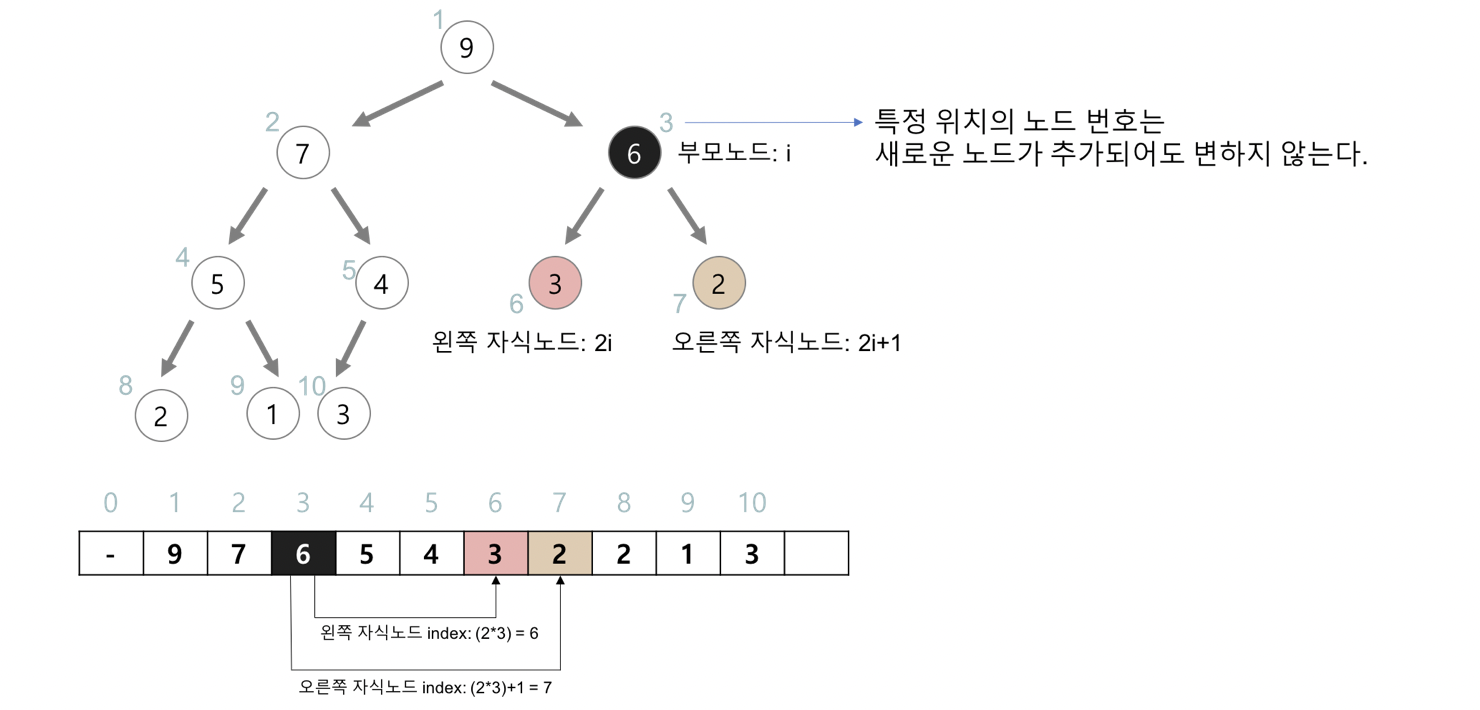
< 힙 트리에서의 자식 노드와 부모 노드와의 관계>

• 왼쪽 자식의 인덱스 = (부모의 인덱스)*2
• 오른쪽 자식의 인덱스 = (부모의 인덱스)*2 + 1
• 부모의 인덱스 = (자식의 인덱스)/2

💻 C++를 이용한 우선순위 큐 프로그래밍

✔︎ STL의 우선순위 큐를 이용한 정렬 함수

#include <queue>
#include <functional>
using namespace std;
// STL의 우선순위 큐를 이용한 내림차순 정렬, 최대힙 사용
void heapSortDec(int a[], int n) {
	priority_queue<int> maxHeap;
	for(int i=0; i<n; i++) {
		maxHeap.push(a[i]);
	}
	// MaxHeap을 이용해 내림차순으로 정렬하기 위한 반복문
	for(int i=0; i<n; i++) {
		a[i] = maxHeap.top();
		maxHeap.pop();
	}
}
// STL의 우선순위 큐를 이용한 오름차순 정렬, 최소힙 사용
void heapSortInc(int a[], int n) {
	priority_queue<int, vector<int>, greater<int>> minHeap;
	for(int i=0; i<n; i++) {
		minHeap.push(a[i]);
	}
	// MinHeap을 이용해 오름차순으로 정렬하기 위한 반복문
	for(int i=0; i<n; i++) {
		a[i] = minHeap.top();
		minHeap.pop();
	}
}

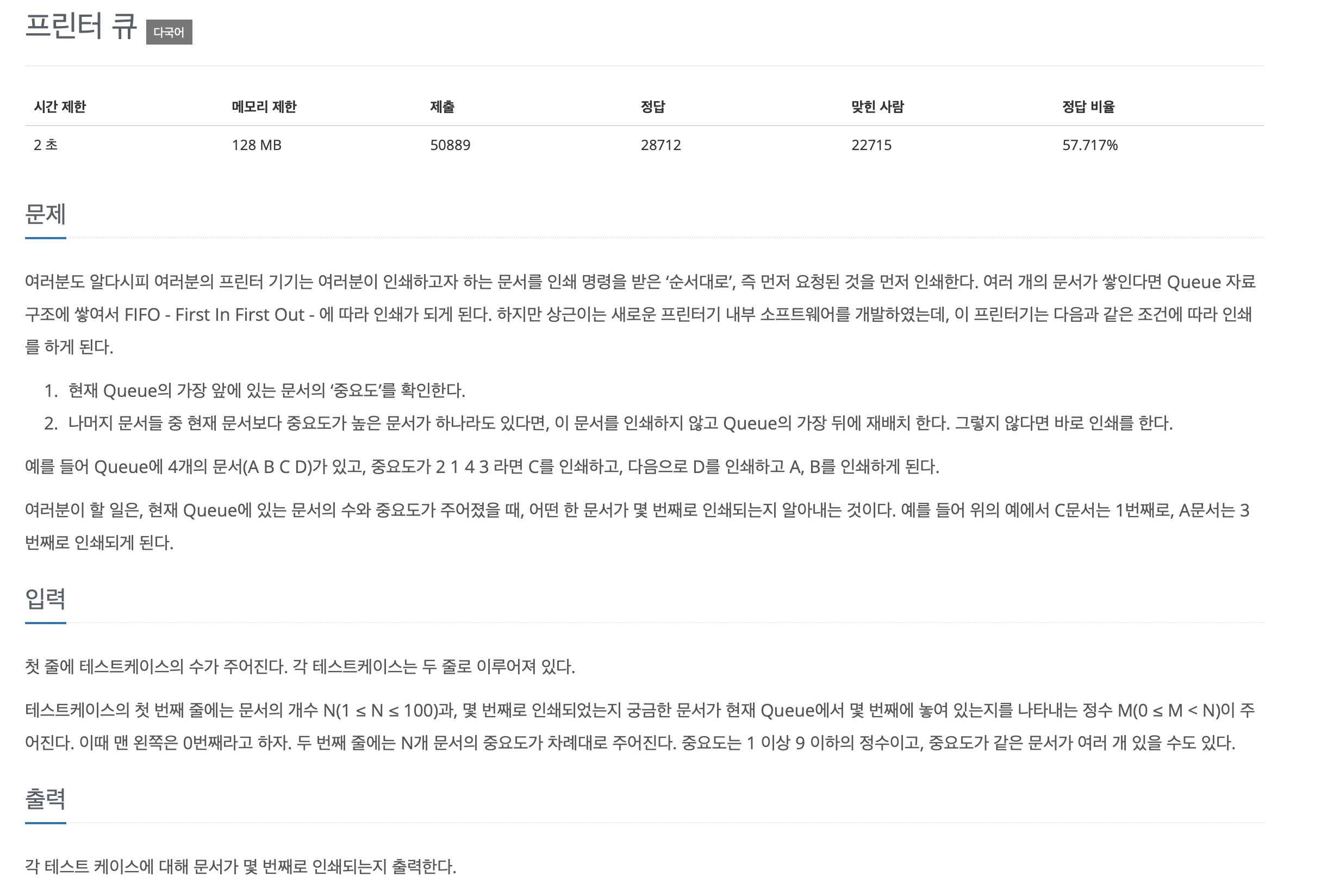
✏️ 백준 1966번

위에서 다룬 내용과 관련된 백준 문제를 풀어보자!

#include <iostream>
#include <queue>
using namespace std;
int main() {
    int count=0;
    int test_case;
    cin >> test_case;
    int n, m,ipt;//문서의 개수, 궁금한 문서 위치, 중요도
    for (int i = 0; i < test_case; ++i) {
        count = 0;
        cin >> n >> m;
        queue<pair<int, int>> q;
        priority_queue<int> pq; // 우선순위 큐
        for (int j = 0; j < n; ++j) {
            cin >> ipt;
            q.push({ j, ipt });
            pq.push(ipt);
        }
        while (!q.empty()) {
            int index = q.front().first;
            int value = q.front().second;
            q.pop();
            if (pq.top() == value) {
                pq.pop();
                ++count;
                if (index == m) {
                    cout << count << endl;
                    break;
                }
            }
            else q.push({ index,value });
        }
    }
}

1. 큐에 인덱스와 그 인덱스에 해당하는 중요도의 값을 넣는다.
2. C++에서 제공하는 STL에서 자동으로 크기가 큰 순으로 정렬 해준다.
3. 큐가 빌 때까지 현재 중요도와 우선순위 큐에 있는 중요도를 확인하고 현재 인덱스와 찾을 인덱스 값이 일치할때까지 갯수를 증가시키며 반복한다.

• 큐 STL 에서 pair 을 사용하면 2개의 데이터를 저장하기 위한 2개의 큐를 동시에 만들 수 있다.