순서

1. 우선순위큐와 힙 내용 정리

2. C++를 이용한 우선순위큐 프로그래밍 방법 정리

3. 백준 1966번 - 프린터 큐

우선순위큐와 힙 내용 정리

우선순위큐 O(n) - 우선순위큐는 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조

• 스택이나 큐를 우선순위큐로 구현 가능
• 배열을 이용한 구현 연결리스트를 이용한 구현, 힙을 이용한 구현이 있음
• 시뮬레이션, 네트워크 트래픽 제어, OS의 작업 스케쥴링 등에 사용

우선순위큐의 데이터

• 우선순위를 가진 요소들의 모음

우선순위큐의 연산

• insert(item) : 우선순위큐에 항목 item을 추가
• remove() : 우선순위 큐로부터 가장 우선순위가 높은 요소를 삭제하고 이 요소를 반환
• find() : 우선순위가 가장 높은 요소를 삭제하지 않고 반환
• isEmpty() : 우선순위큐가 공백상태인지 검사
• isFull() : 우선순위큐가 포화상태인지 검사
• display() : 우선순위큐의 모든 요소를 출력

힙(Heap) - 완전이진트리 형태의 자료구조

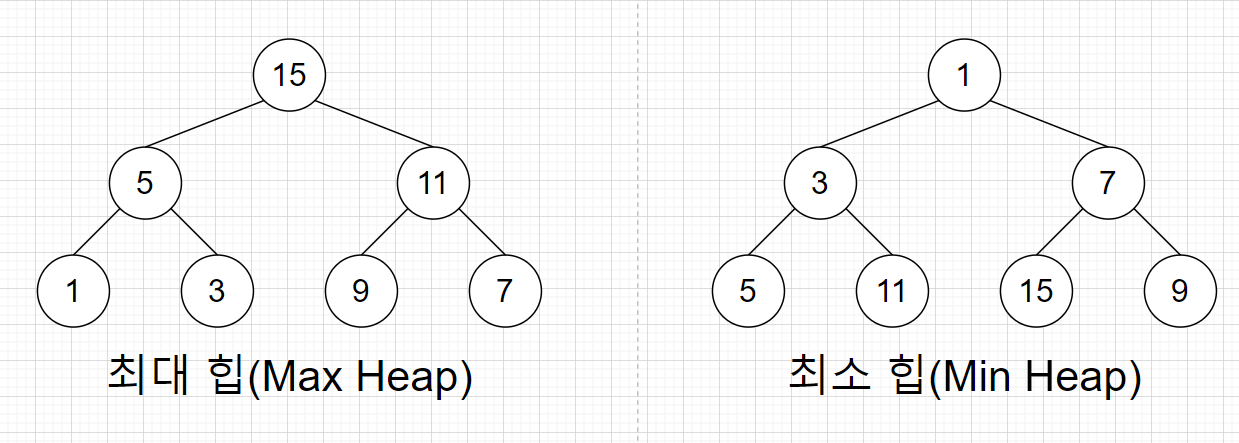
최대 힙(Max Heap)
: 부모 노드의 key값이 자식 노드의 key값보다 크거나 같은 완전 이진 트리

최소 힙(Min Heap)
: 부모 노드의 key값이 자식 노드의 key값보다 작거나 같은 완전 이진 트리

힙의 높이

• n개의 노드를 가지고 있는 힙의 높이는 O(logn)
  : 마지막 레벨을 제외하고 각 레벨 i에 2**i -1개의 노드가 존재

힙의 구현
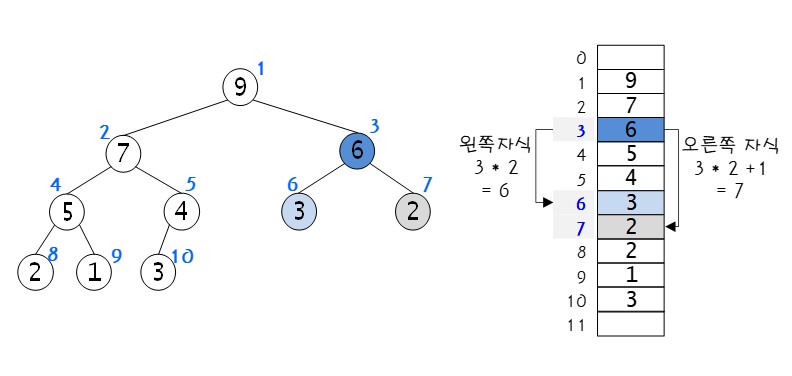
: 배열을 이용해 힙을 구현할 수 있음

• 부모 노드와 자식 노드의 관계
  : 왼쪽 자식의 인덱스 = (부모의 인덱스)2
  : 오른쪽 자식의 인덱스 = (부모의 인덱스)2 + 1
  : 부모의 인덱스 = (자신의 인덱스)/2

삽입 연산

• Upheap
  : 삽입된 노드에서 루트까지의 경로에 있는 노드들을 비교/교환
  : 히프의 성질을 복원(key가 부모노드보다 작거나 같으면 upheap을 종료)

삭제 연산

• 최대힙에서의 삭제 -> 항상 루트가 삭제됨
  (가장 큰 키 값을 가진 노드를 삭제하는 것)
• Downheap
  : 루트 삭제
  : 루트에서부터 단말노드까지의 경로에 있는 노드들을 교환하여 히프 성질을 만족시킴

힙의 복잡도

• 삽입연산에서의 최악의 경우
  : O(logn)
• 삭제연산에서의 최악의 경우
  : O(logn)
  -> 두 경우 모두 트리의 높이에 해당하는 비교 연산 및 이동 연산이 필요

C++를 이용한 우선순위큐 프로그래밍 방법 정리

#include <iostream>
#include <queue>
using namespace std;

int main()
{
	priority_queue<int> pq; // 우선순위 큐 선언
    
    pq.push(9);
    pq.push(3);
    pq.push(7);
    pq.push(1);
    pq.push(10); // 우선순위 큐에 원소 삽입
    
    cout << pq.size() << endl; // 결과 출력
    
    while(!pq.empty()) // 우선순위 큐가 비어있지 않다면 반복문 실행
    {
    	int temp = pq.top(); // 큐의 제일 앞부분 값 불러오기
        cout << temp; // 큐 제일 앞부분 빼기
        pq.pop();
    }
    return 0;
}

백준 1966번 - 프린터 큐

#include <iostream>
#include <queue>
using namespace std;

int main()
{
	int n, m = 0; // 문서 개수, 문서 위치
    int imp; // 중요도
    int cnt = 0;
    int test_case; // 
    
    cin >> test_case;
    for (int i = 0; i < test_case; i++)
    {
    	cin >> n >> m;
        queue<pair<int, int>> q;
        priority_queue <int> pq;
        
        for (int j = 0; j < n; ++j)
        {
        	cin >> imp;
            q.push({ j,imp });
            pq.push(imp);
        }
        while (!q.empty())
        {
        	int index = q.front().first;
            int value = q.front().second;
            q.pop();
            
            if(pq.top() == value)
            {
            	pq.pop();
                cnt++;
                if (index == m)
                {
                	cout << cnt << endl;
                    break;
                }
            }
        }   
        else q.push({ index,value });
    }
}