순서
-
스케줄링 문제에 접근하는 이진 탐색 트리 소개
-
Big-O 소개
-
LeetCode 98, 99, 700, 701 풀이
스케줄링 문제에 접근하는 이진 탐색 트리 소개
탐색(search) : 가장 중요한 컴퓨터 응용의 하나
이진탐색트리(BST) : 이진트리 기반의 효율적인 탐색 작업을 위한 자료구조
탐색 관련 용어
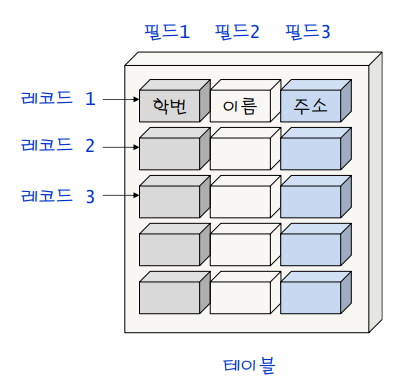
- 레코드 : 개체에 대해 수집된 모든 정보를 포함하고 있는 저장 단위
- 필드 : 레코드에서 각각의 정보를 나타내는 부분
- 테이블 : 레코드들의 집합
- 키 : 중복되지 않은 고유한 값
- 주요키 : 중복되지 않은 고유한 값, 각 레코드를 구별할 수 있음
이진탐색트리의 정의
- key(왼쪽서브트리) ≤ key(루트노드) ≤ key(오른쪽서브트리)
(이진탐색을 중위순외하면 오름차순으로 정렬된 값을 얻을 수 있음)
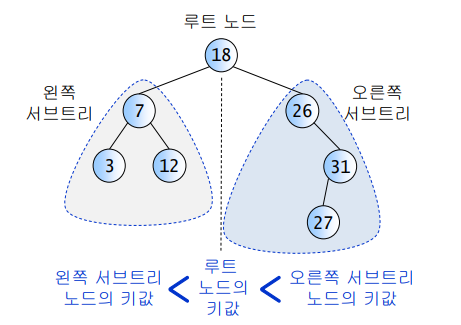-> 예) 3, 7, 12, 18, 26, 27, 31
이진탐색트리의 연산
<연산 정리>
- insert(n) : 이진탐색트리의 특성을 유지하면서 새로운 노드 n을 이진탐색트리에 삽입한다.
- remove(n) : 이진탐색트리의 특성을 유지하면서 노트 n을 트리에서 삭제한다.
- search(key) : 키 값이 key인 노드를 찾아 반환한다.
탐색연산
- 비교한 결과가 같으면 탐색이 성공적으로 끝남
- 키 값이 루트보다 작으면 -> 왼쪽 자식을 기준으로 다시 탐색
- 키 값이 루트보다 크면 -> 오른쪽 자식을 기준으로 다시 탐색
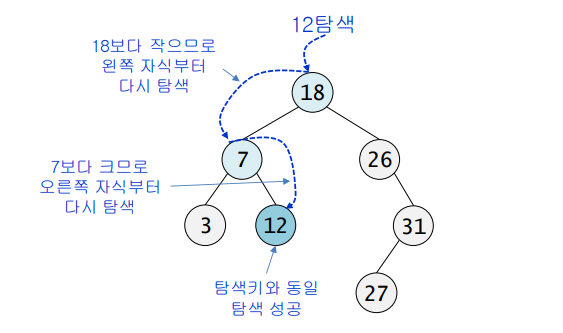
탐색연산의 구현
- 순환적인 일반함수 구현
- 반복적인 일반함수 구현
- 노드의 멤버함수로 구현(순환적)
삽입연산
- 이진탐색트리에 원소를 삽입하기 위해서 먼저 탐색을 수행하는 것이 필요함
- 탐색에 필요한 위치가 바로 새로운 노드를 삽입하는 위치
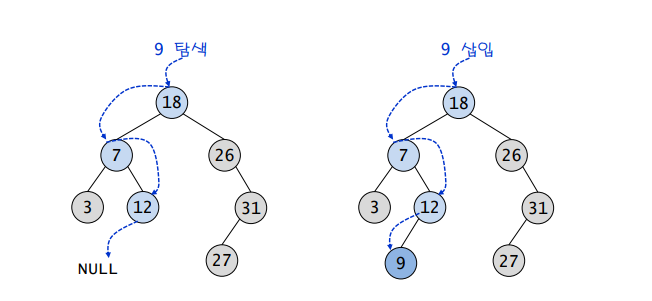
삭제연산
<노드삭제의 3가지 경우>
-
삭제하려는 노드가 단말 노드일 경우 - 단말노드의 부모노드를 찾아서 연결을 끊으면 됨
-
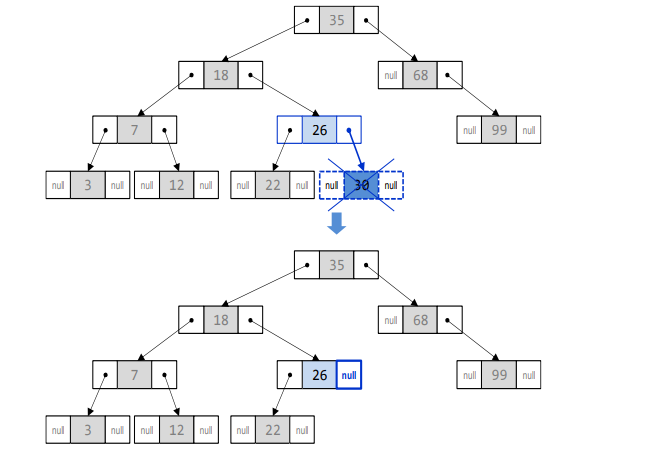
삭제하려는 노드가 왼쪽/오른쪽 서브 트리 중 하나만 가지고 있는 경우 - 노드는 삭제하고 서브 트리는 부모 노드에 붙여주면 됨
-
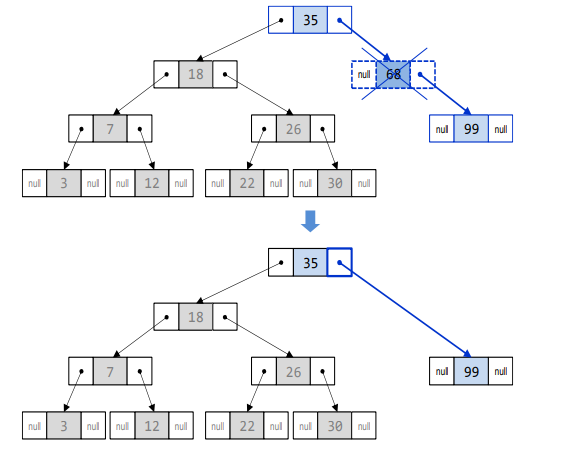
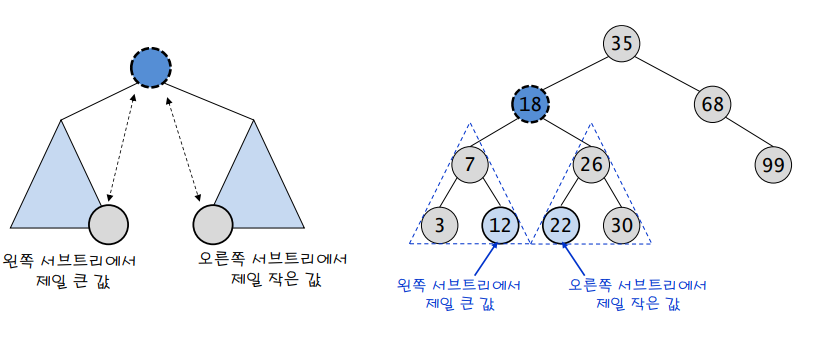
삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우 - 가장 비슷한 값을 가진 노드를 삭제 노드 위치로 가져오면 됨
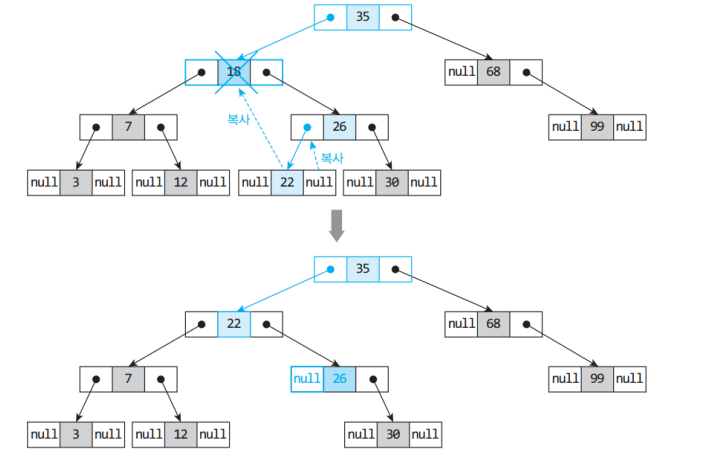
후계 노드의 선택 : 왼쪽 서브트리에서 제일 큰 값, 오른쪽 서브트리에서 제일 작은 값
이진탐색트리의 성능
: 이진탐색트리에서의 탐색, 삽입, 삭제 연산의 시간 복잡도는 트리의 높이를 h라고 했을 때 h에 비례한다.
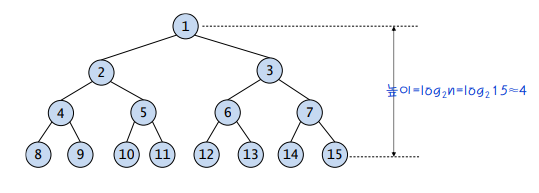
최선의 경우 : 이진 트리가 균형적으로 생성되어 있는 경우(h = log2n)
-> 시간복잡도 : O(logn)
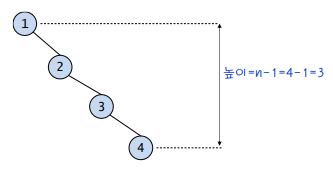
최악의 경우 : 경사이진트리인 경우(h = n)
-> 시간복잡도 : O(n)
Big-O 소개
Big-O 표기법의 정의
: 알고리즘의 시간복잡도를 나타내는 표기법이며, O(f(n))로 나타낸다.
알고리즘의 복잡도를 판단하는 척도 = 시간복잡도/공간복잡도
그 중 시간복잡도를 다루는 것이 빅오표기법임
-> 알고리즘은 연산이 많아질수록 속도가 오래걸리기 때문에 시간복잡도는 알고리즘 내의 연산횟수와 연관이 있다.
Big-O 표기법의 법칙
1. f(n)이 n에 대한 d차식이면, f(n)은 O(n^d)이다.
2. 가능한 가장 작은 notation을 사용하여야 한다.
=> O(n^2)도 되고 O(n)도 된다면 가장 작은 O(n)을 사용
3. 가능한 가장 간단한 표기를 사용하여야 한다.
=> O(3n+4)도 되고 O(n)도 된다면 가장 간단한 O(n)을 사용
Big-O표기법의 시간 복잡도(알고리즘의 복잡도) 비교
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n)
*복잡한 순서대로임
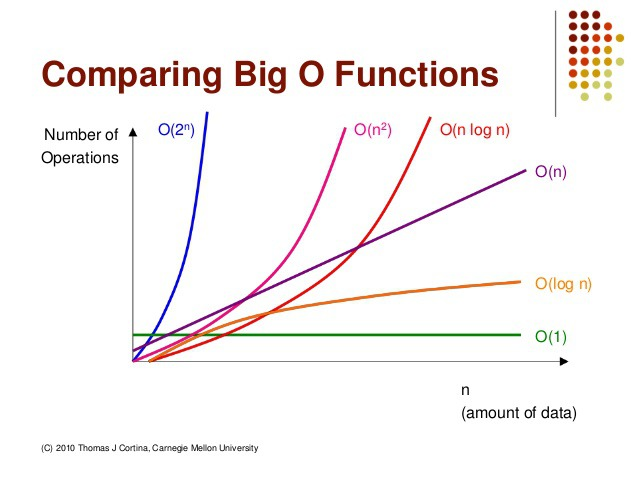
Big-O표기법의 특징
1. 상수항 무시
: 데이터 입력값(n)이 충분히 크다고 가정하고 있고, 알고리즘의 효율성 또한 데이터 입력값의 크기에 따라 영향을 받기 때문에 상수항과 같은 사소한 부분은 무시한다.
2. 영향력 없는 항 무시
: 가장 영향력이 큰 항 이외에 영향력이 없는 항들은 무시한다.
LeetCode 98, 99, 700, 701 풀이
98번 Validate Binary Search Tree
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
-The left subtree of a node contains only nodes with keys less than the node's key.
-The right subtree of a node contains only nodes with keys greater than the node's key.
-Both the left and right subtrees must also be binary search trees.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public boolen isValidBST(TreeNode root)
{
return checkBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolen checkBST(TreeNode root, long min, long max)
{
if(root==NULL)
{
return true;
}
if(root.val <= min || root.val >= max)
{
return false;
}
return checkBST(root.left, min, root.val) && checkBST(root.right, root.val, max);
}
}
99번 Recover Binary Search Tree
You are given the root of a binary search tree (BST), where the values of exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public:
void recoverTree(TreeNode* root)
{
inorder(root);
swap(x,y);
}
private:
TreeNode* pred = nullptr;
TreeNode* x = nullptr;
TreeNode* y = nullptr;
void inorder(TreeNode* root)
{
if(!root)
return;
inorder(root->left);
if(pred && root->val < pred->val)
{
y = root;
if(!x)
x = pred;
else
return;
}
pred = root;
inorder(root->right);
}
void swap(TreeNode* x, TreeNode* y)
{
const int temp = x->val;
x->val = y->val;
y->val = temp;
}
};700번 Search in a Binary Search Tree
You are given the root of a binary search tree (BST) and an integer val.
Find the node in the BST that the node's value equals val and return the subtree rooted with that node. If such a node does not exist, return null.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public TreeNode searchBST(TreeNode root, int val)
{
return findNode(root, val);
}
private TreeNode findNode(TreeNode node, int val)
{
if (node == null || node.val == val)
{
return node;
}
if (node.val > val)
{
return findNode(node.left, val);
}
else
{
return findNode(node.right, val);
}
}
}701번 Insert into a Binary Search Tree
You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.
Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public TreeNode insertIntoBST(TreeNode root, int val)
{
if (root == null)
{
return new TreeNode(val);
}
traverseBST(root, val);
return root;
}
private void traverseBST(TreeNode node, int val)
{
if (val < node.val)
{
if (node.left == null)
{
node.left = new TreeNode(val);
}
else
{
traverseBST(node.left, val);
}
}
else if (val > node.val)
{
if (node.right == null)
{
node.right = new TreeNode(val);
}
else
{
traverseBST(node.right, val);
}
}
else
{
return;
}
}
}
