순서

1. Data structures augmentation 코딩
   • Rank 구현
2. AVL Tree 정의 등 강의 내용 정리
   • AVL Tree 구현
3. LeetCode 110 풀이

Data structures augmentation 코딩

Rank 구현

• Rank의 정의 : 임의의 행렬 A가 있을 때, 이 행렬의 Rank 라는 것은 이 행렬의 열들로 생성될 수 있는 벡터 공간의 차원을 의미한다. (이진 탐색 트리에서의 Rank는 찾는 노드 이전에 노드가 몇개 있는지 알 수 있게 해주며 이진트리의 구조를 균형있게 만든다.)

• Rank의 특징 : Rank는 여러가지 방법으로 붙일 수 있고, 아래의 규칙에 따라 Rank를 붙이며 트리 탐색을 할 수 있다.
  - 1. rank 가 가장 큰 노드를 고른다.
  - 2. 답으로 나온 서브트리에 대해서 1번을 반복한다.

• Rank 코드

public int size() 
{
	if(root==null)         
    	return 0;
    else 
        return rSize(root); //returns recursive size method below
}

    private int rSize(Node node)
    {
        if(node==null)
        	return 0;
        else 
            return (rSize(node.left) + rSize(node.right) + 1);
    }

    public Key rank(int k) 
    {
        Node node = select(root, k);
        if (node==null)
            return null;
        else 
            return node.key;
    }   

    private Node rank(Node node, int k) 
    { 
        if (node == null) return null;

        int t = rSize(node.left);
        if (t > k)
            return select(node.left, k);
        else if (t < k)
            return select(node.right, k - t - 1);
        else
            return node;
    }

AVL Tree 정의 등 강의 내용 정리

AVL Tree 정의

-> 모든 노드에 대해 왼쪽 및 오른쪽 트리의 높이 차이가 하나 이상일 수 없는 자체 균형 이진 검색 트리(BST)이다.

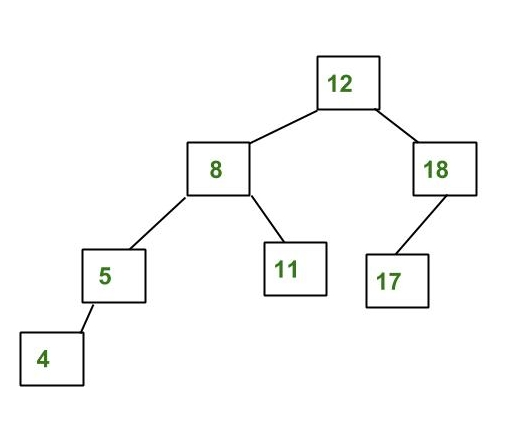
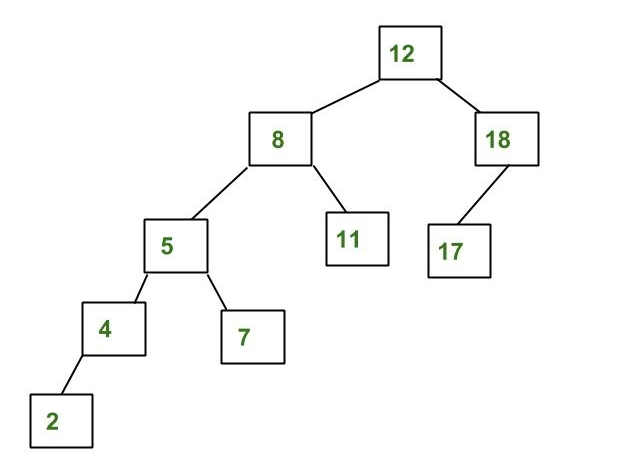
AVL Tree 예시

-> 왼쪽과 오른쪽 하위 트리의 높이 차이가 1보다 작거나 같으므로 AVL Tree가 맞음

-> 8과 12에 대한 왼쪽 하위 트리의 높이 차이가 1보다 크므로 AVL Tree가 아님

AVL Tree 특징

• 이진 탐색 트리의 특징을 가진다.
• 왼쪽/오른쪽 높이 차이가 1 이상이 되면 회전을 통해 균형을 잡는다.
• 높이를 logN으로 유지하므로 시간복잡도는 O(logN)이 된다.

AVL Tree 시간복잡도

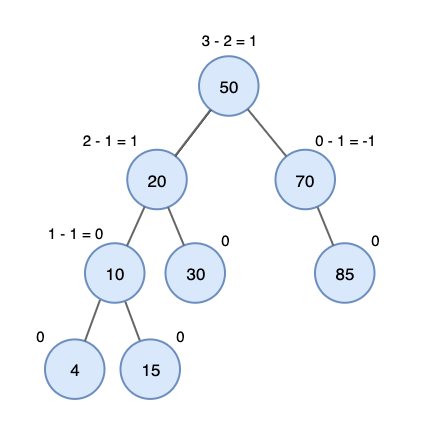
Balance Factor(BF)

-> 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 값

Balance Factor (k) = height (left(k)) - height(right(k))

• BF가 1 = 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 높다는 것을 의미
• BF가 0 = 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같다는 것을 의미
• BF가 -1 = 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 낮다는 것을 의미
  

AVL Tree에서 BF가 안 맞을때 BF를 유지하는 방법 : 회전(Rotation)

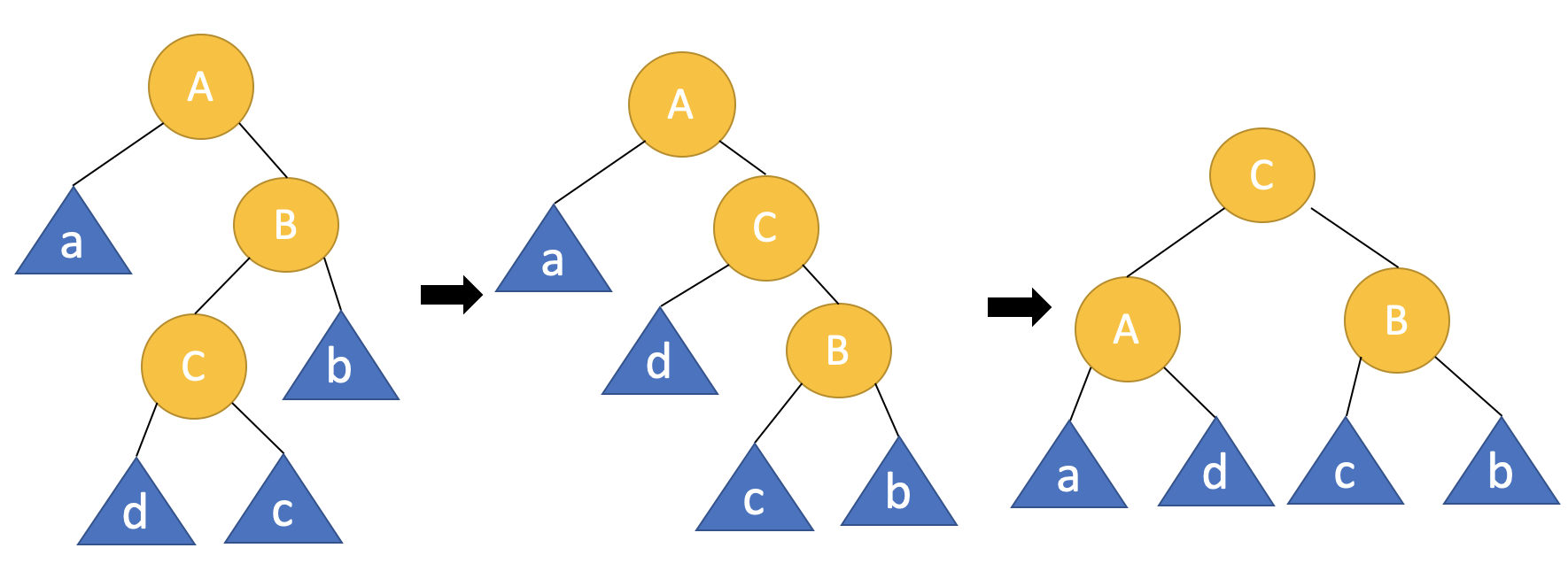
1. left rotation

a, b, c는 서브트리를 의미하며 서브트리는 노드가 단 1개일수도 혹은 비어있을 수도 있다. 회전 기준은 노드 A이다.

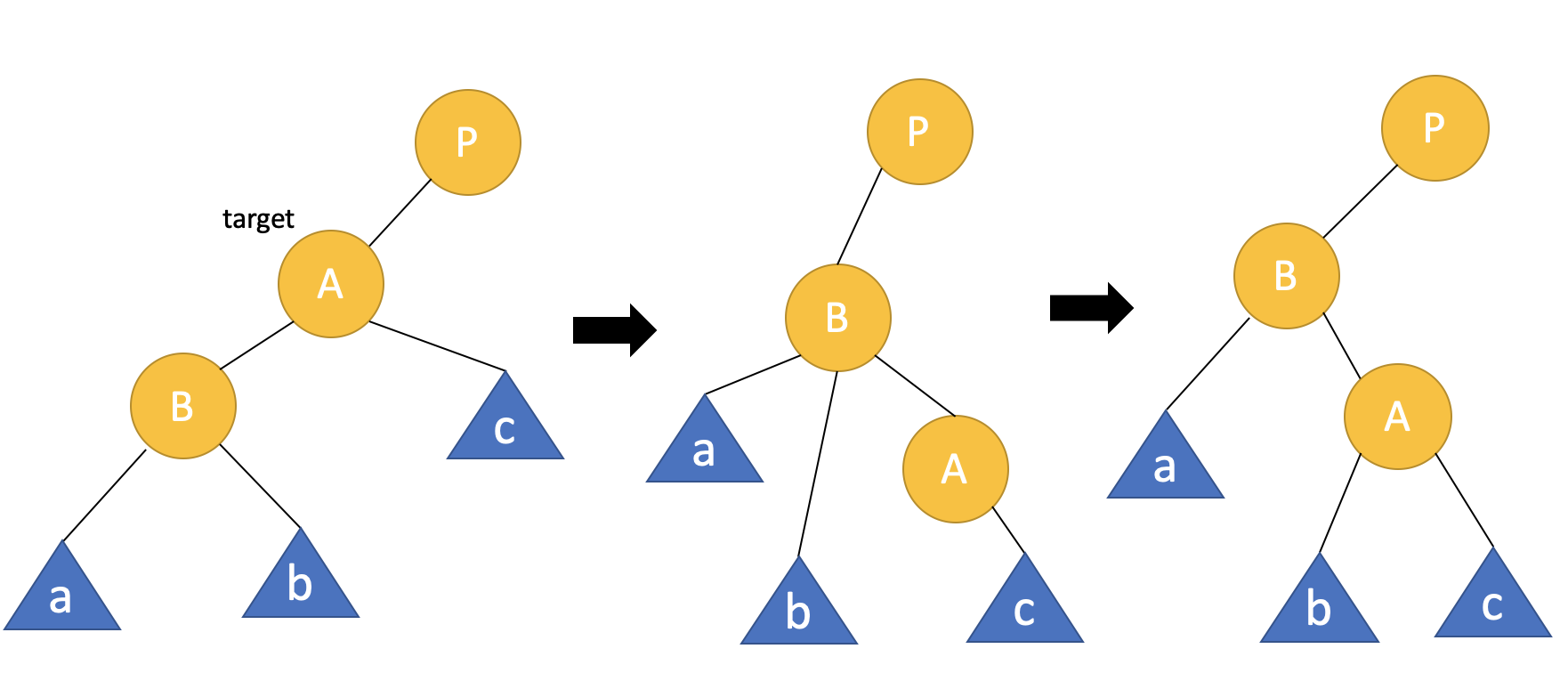
회전하면서 노드 A의 위치를 노드 B가 대신하고, 그 과정에서 노드 B의 자식이 3개가 되기 때문에 서브트리 b의 위치를 조정한다.

2. right rotation

위와 마찬가지로 a, b, c는 서브트리, 회전기준은 노드 A이다.

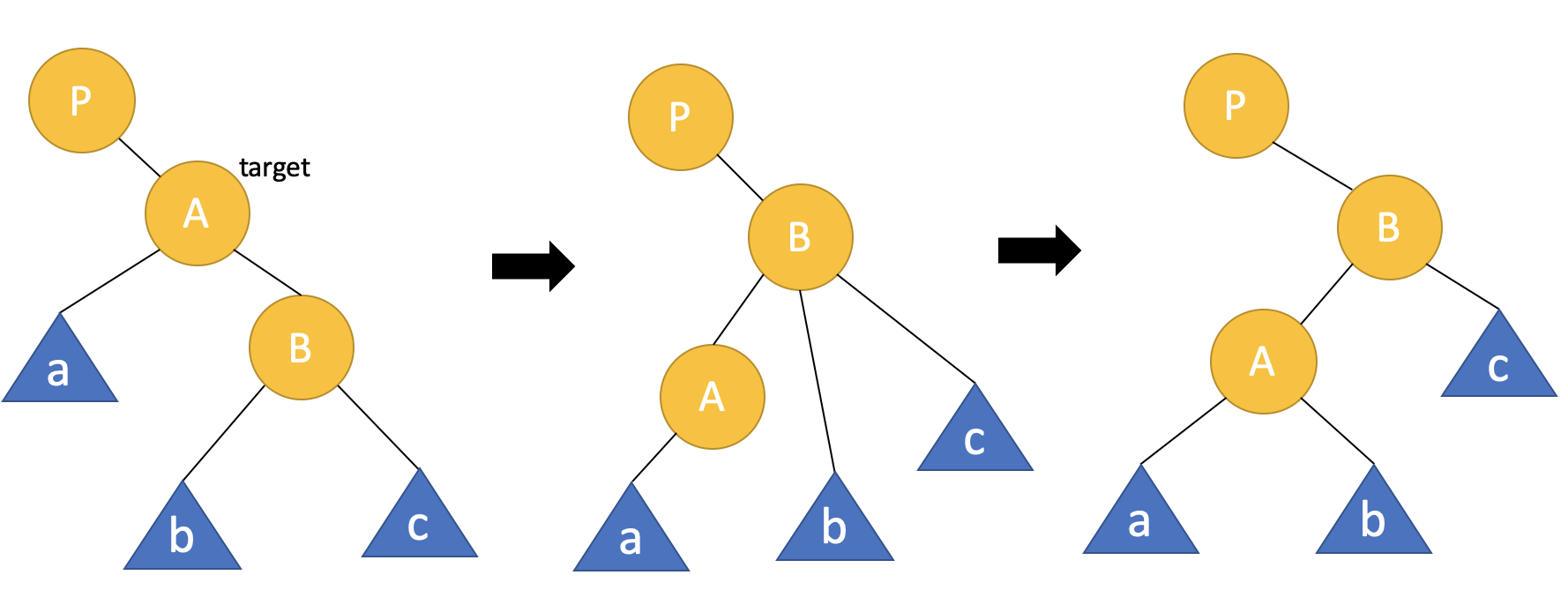
노드 A의 위치를 노드 B가 대신하고 서브트리 b의 위치를 조정한다.

left rotation과 right rotation을 적용하는 4가지의 경우

1. Left-Left (LL)

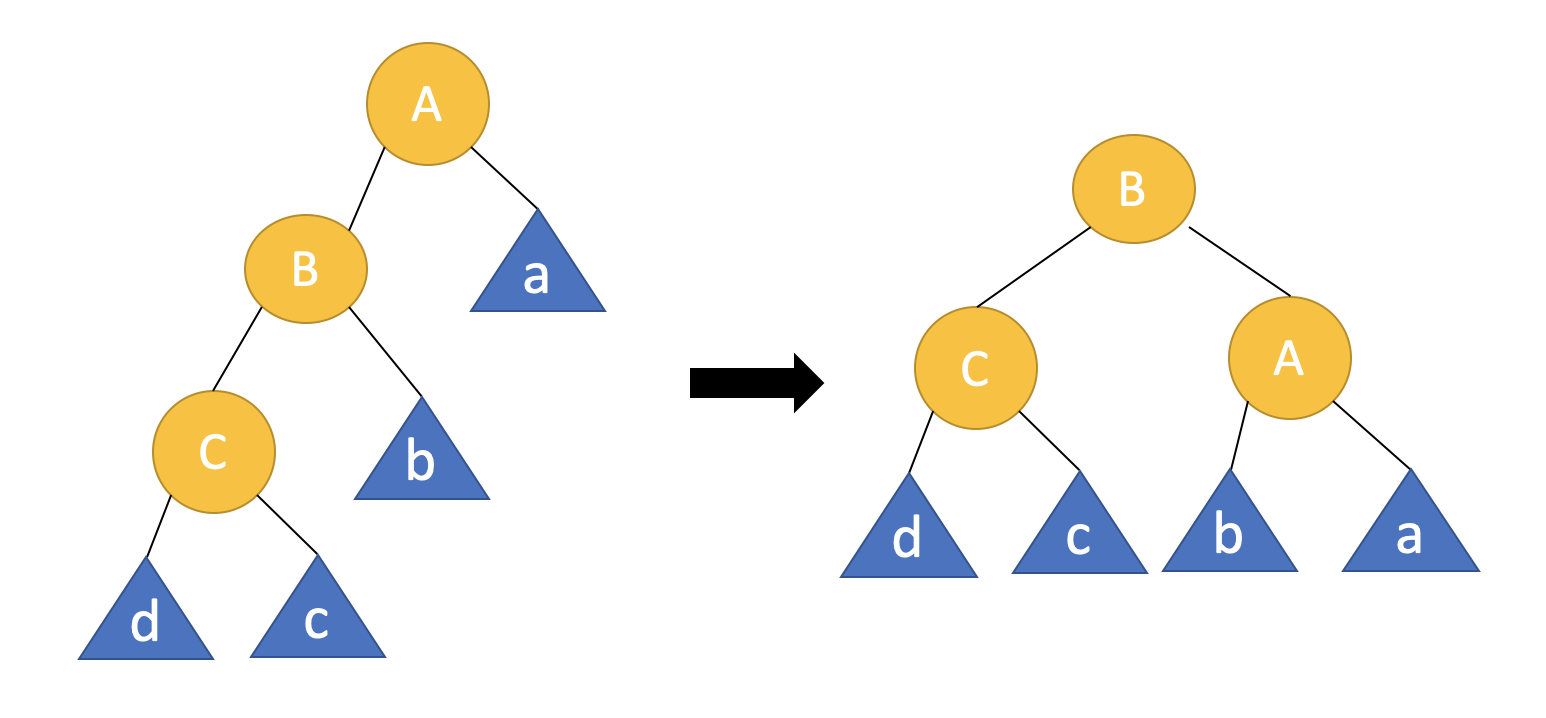
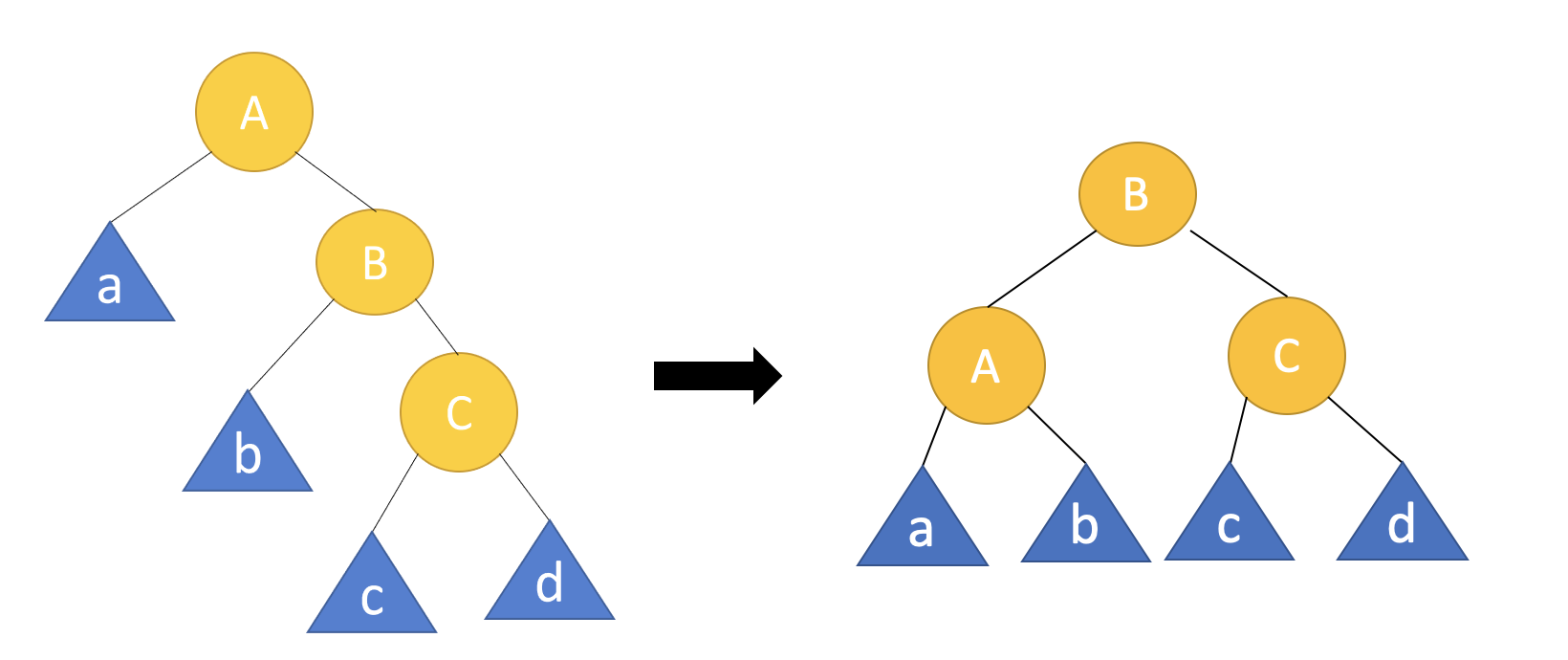
2. Right-Right (RR)

3. Left-Right(LR)

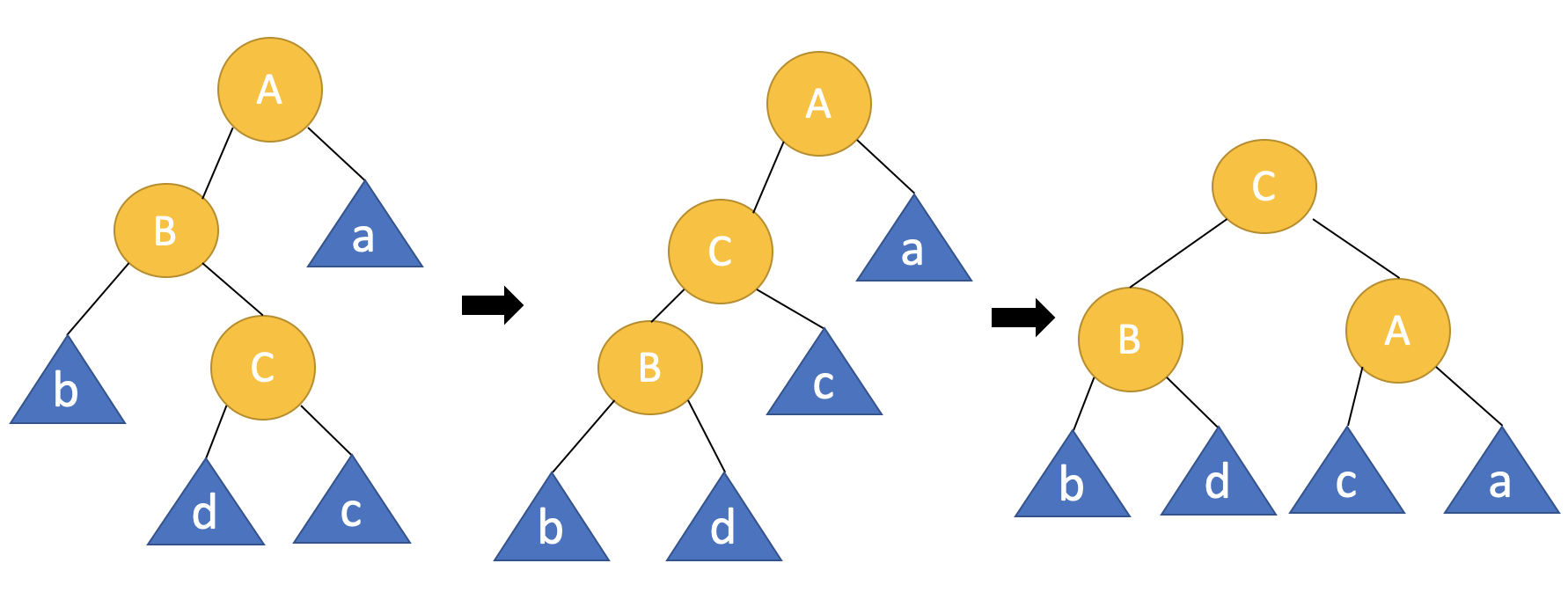
4. Right-Left(RL)

AVL Tree 구현

위에 설명한 4가지 rotation 함수 구현

1. Left-Left (LL)

BinaryTreeNode * rotateLL (BinaryTreeNode * pTree) {
    BinaryTreeNode * parent = pTree;
    BinaryTreeNode * child = GetLeftSubTree(parent);
    ChangeLeftSubTree(parent, GetRightSubTree(child));
    ChangeRightSubTree(child, parent);
    return child;   
}

2. Right-Right (RR)

BinaryTreeNode * rotateRR (BinaryTreeNode * pTree) {
    BinaryTreeNode * parent = pTree;
    BinaryTreeNode * child = GetRightSubTree(parent);
    ChangeRightSubTree(parent, GetLeftSubTree(child));
    ChangeLeftSubTree(child, parent);
    return child;  
}

3. Left-Right(LR)

BinaryTreeNode * rotateLR (BinaryTreeNode * pTree) {
    BinaryTreeNode * parent = pTree;
    BinaryTreeNode * child = GetLeftSubTree(parent);
    ChangeLeftSubTree(parent, rotateRR(child));
    return rotateLL(parent);
}

4. Right-Left(RL)

BinaryTreeNode * rotateRL (BinaryTreeNode * pTree) {
    BinaryTreeNode * parent = pTree;
    BinaryTreeNode * child = GetLeftSubTree(parent);
    ChangeRightSubTree(parent, rotateLL(child));
    return rotateRR(parent);
}

LeetCode 110 풀이

110. Balanced Binary Tree

Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
 
 class Solution 
 {
    public boolean isBalanced(TreeNode root) 
    {
        if(root == null)
        {
        	return true;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        
        if(Math.abs(leftHeight - rightHeight) > 1)
        {
            return false;
        }
        return isBalanced(root.left) && isBalanced(root.right);
    }
    private static int getHeight(TreeNode node)
    {
        if(node == null) return 1;
        {
        	return Math.max(getHeight(node.left), getHeight(node.right)) + 1;
        }
    }
}

참고자료) Geeks for geeks
https://www.geeksforgeeks.org/avl-tree-set-1-insertion/
https://www.geeksforgeeks.org/avl-tree-set-2-deletion/