Language Modeling : Generalization, Smoothing, Interpolation, Good-Turing Smoothing, Kneser
NLP
N-gram Modeling을 할 때 Count형식으로 확률을 계산하면 거의 0이 나온다.
Generalization
Bi-gram with zeros
샤넌 시각화 방법은 우리가 만든 n-gram model에 대해 여러 가지 정보를 제공한다.
가령, 셰익스피어를 기반으로 생성된 모델을 살펴보자.


문제는, 셰익스 피어 내에 존재하는 bi-gram은 30만개인데 반해, voca로 미루어봤을 때 가능한 수는 8억개가 넘는다.
반면, wall-street journal의 corpus를 생각해보자.

그 후 셰익스피어와 월스트리트 저널을 비교해보자.
두 corpus는 충분한 단어들이 있지만, 셰익스피어와 월스트리트 저널 간에 겹치는 문장은 아예 없다.
그렇다는 것은, 어느 하나에만 학습시켰을 경우 과적합의 위험성이 있다는 것이다.
(셰익스피어에 학습시킨 모델은 월스트리트 저널에 잘 작동할 수 없다.)
이런 과적합을 피하기 위해 우리는 일반화에 대한 고려를 해야하고, 그 대안으로 취할 수 있는 방법은 zeros를 다루는 것이다.
즉, train set에는 없지만, test set에는 나타나는 단어를 다룰 필요가 있다.

위처럼, Test set에 처음 나타나는 단어의 확률은 0일수밖에 없다.
그 말은, Zero probability bigrams에 대해서는 Perplexity를 계산할 수 없다는 것이다.
(0으로는 나눌 수 없으므로)
Add-one Smoothing(Laplace smoothing)
아무튼, 가장 대표적으로 위의 Zeros problem을 다루는 방법은 제로가 없게끔 확률을 조금씩 smoothing 해주는 것입니다.
즉, 카운트를 기본적으로 1씩 더해주면 add-one smoothing이됩니다.
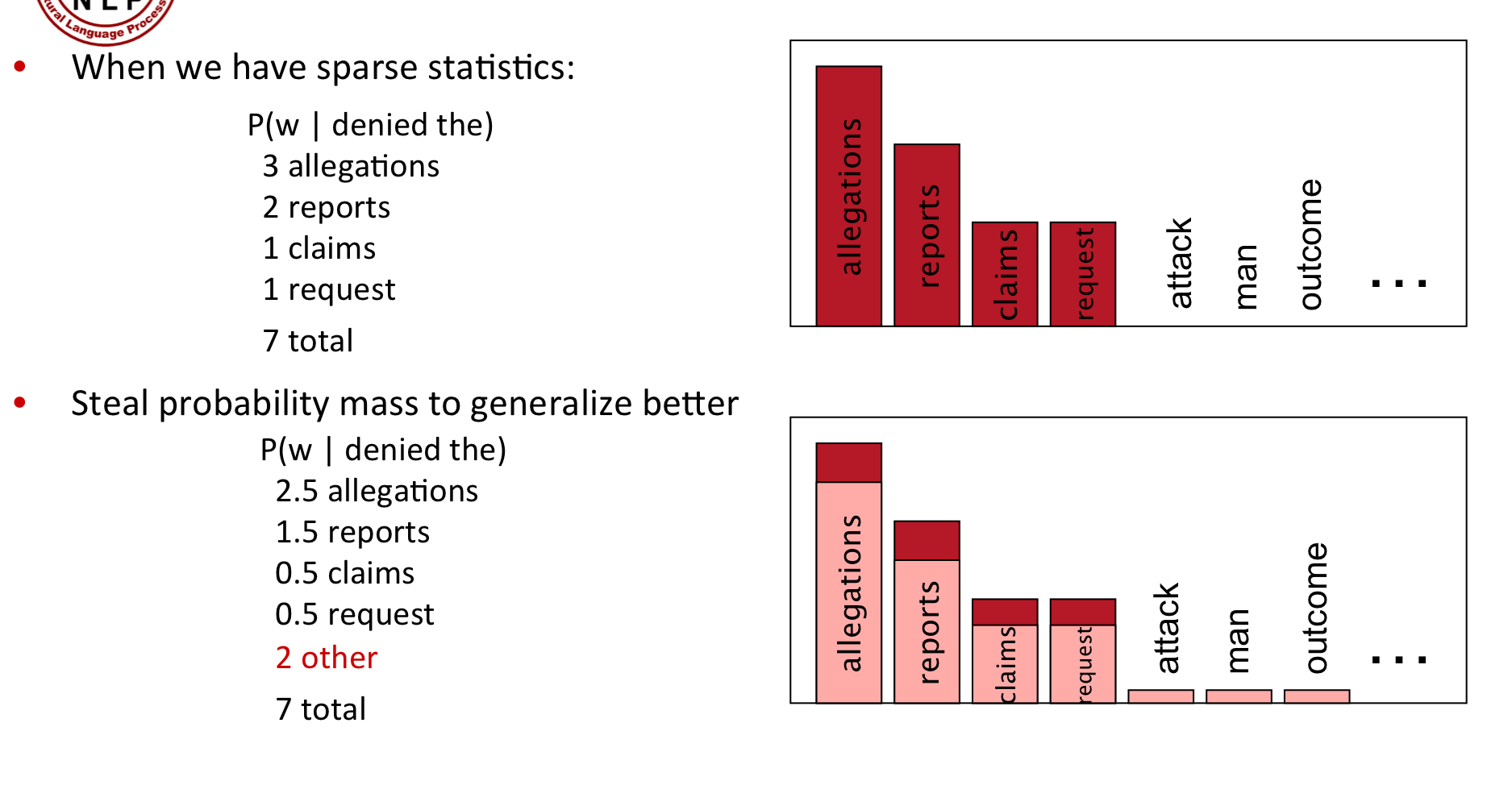
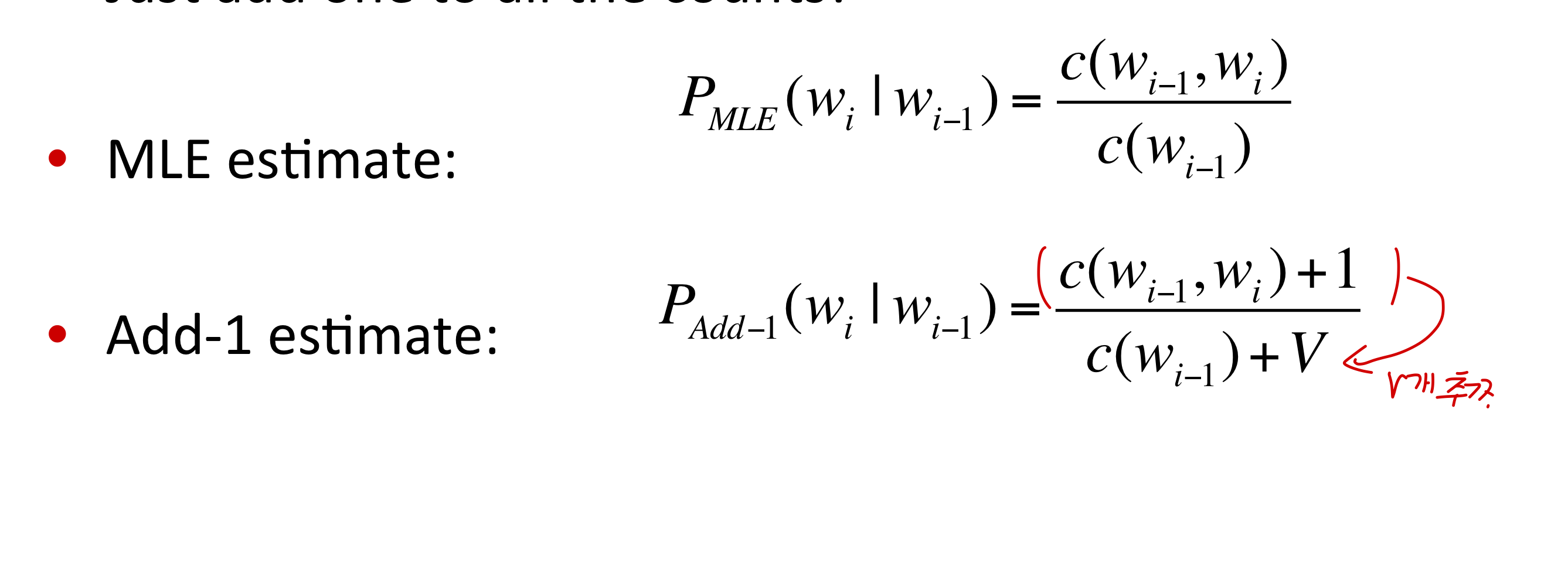
Bi-gram을 1씩 더하면, 그 안에 포함된 Unigram은 가능한 voca의 개수만큼 늘어나겠죠.
MLE?
다만, 위에서 MLE에 대한 얘기가 나옵니다.
MLE에 대한 기본적인 개념은 차치하고, Add-one Smoothing을 진행하게 되면 기존의 MLE(트레이닝 데이터를 기반으로 가장 그럴싸한 추정치)랑은 달라지게 됩니다.

다른 smoothing 방법들도 모두 non-maximum likelihood estimates입니다.
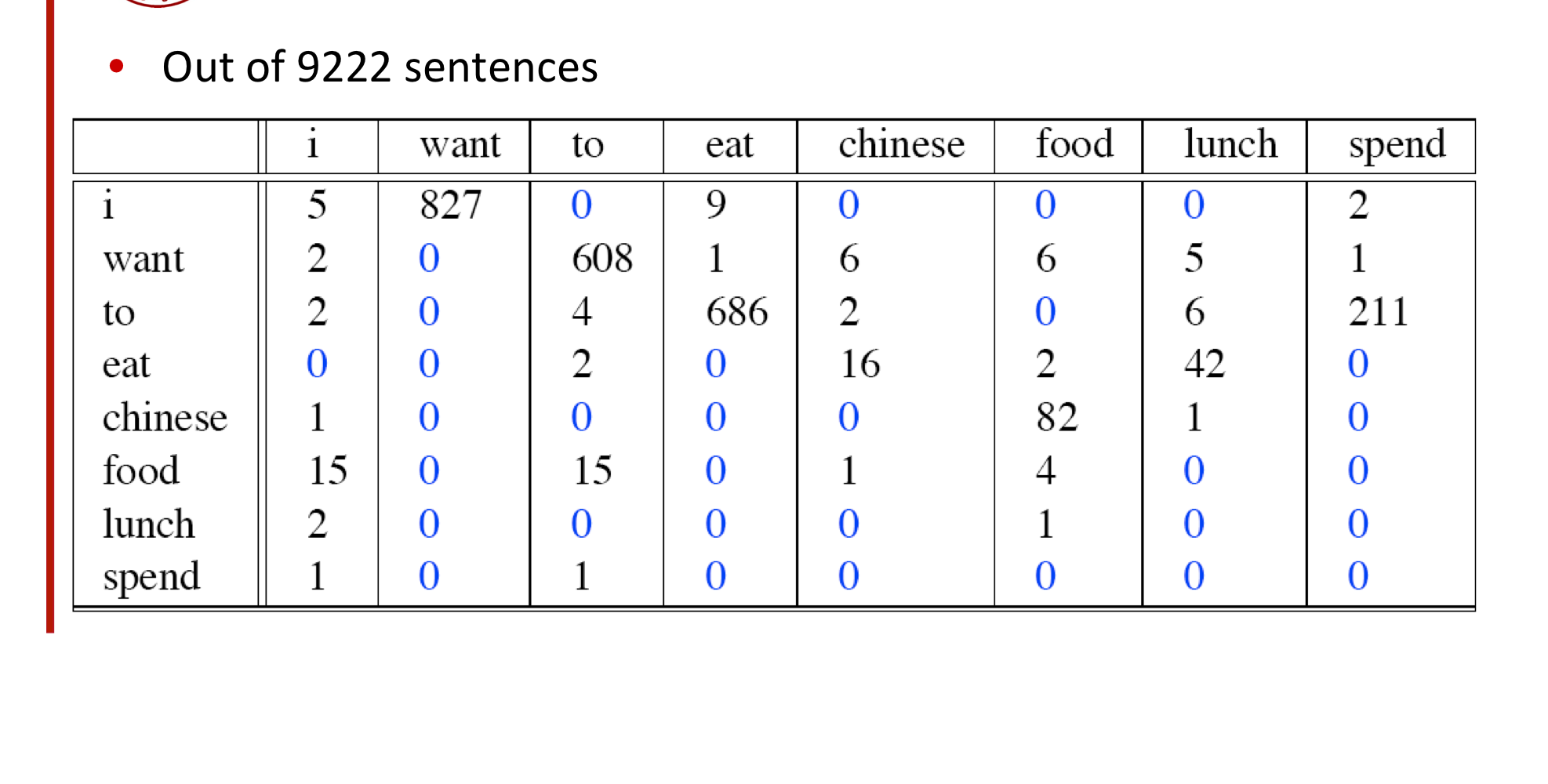
Laplace smothed bigram counts
아무튼, 위와 같이 나오지 않은 단어들에 대해 1씩 count를 더하게 되면, 위와 같이 새로운 확률을 계산할 수 있습니다.
기존
변경
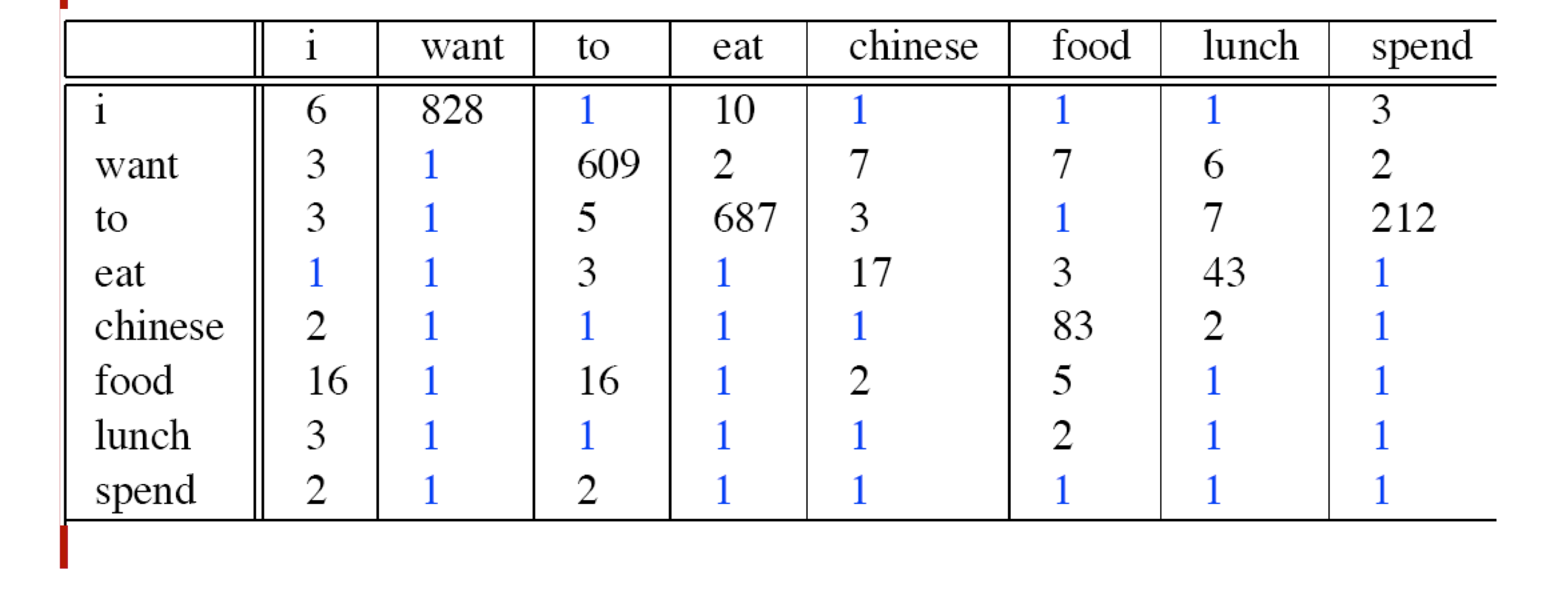
기존
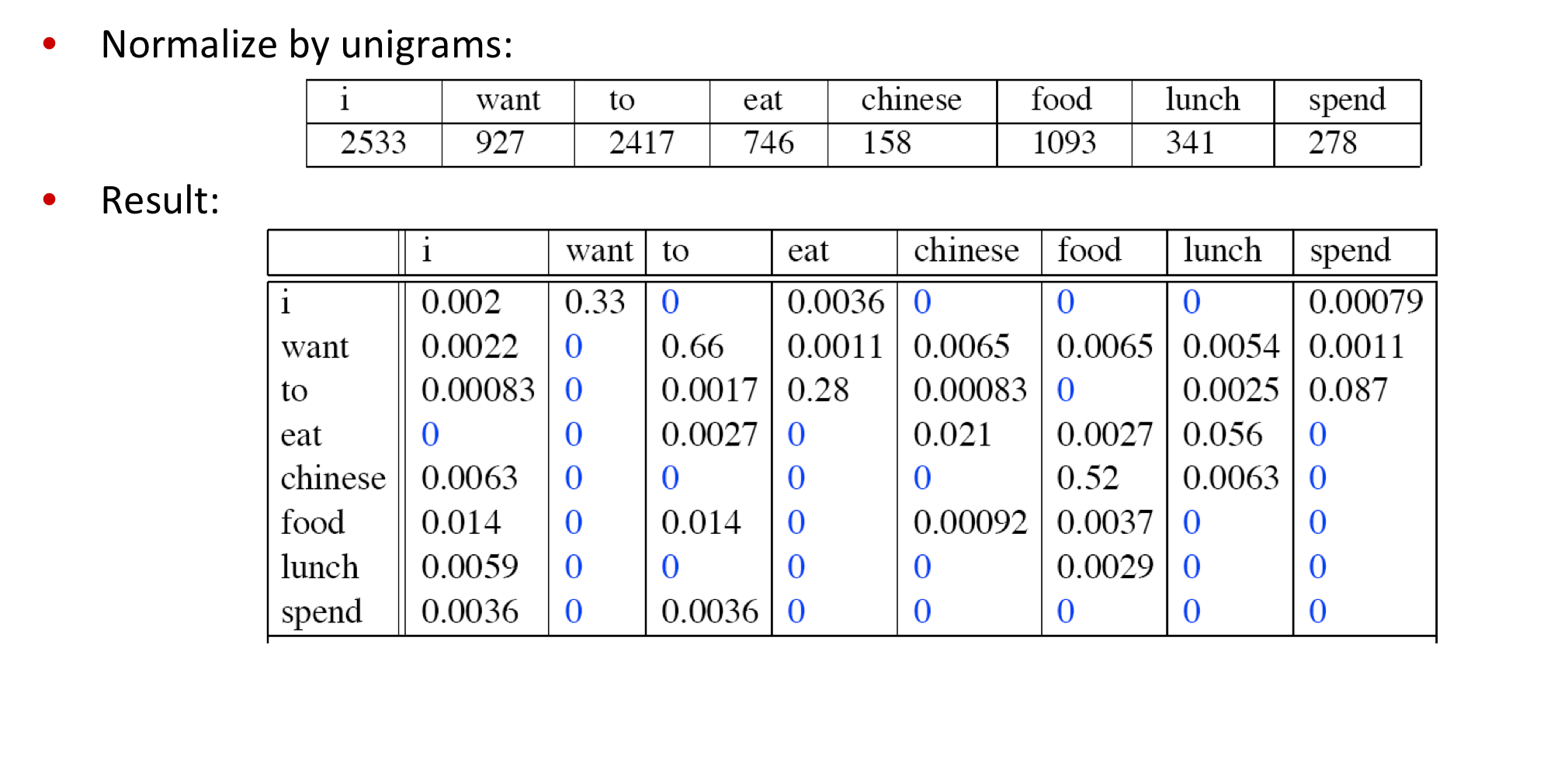
변경
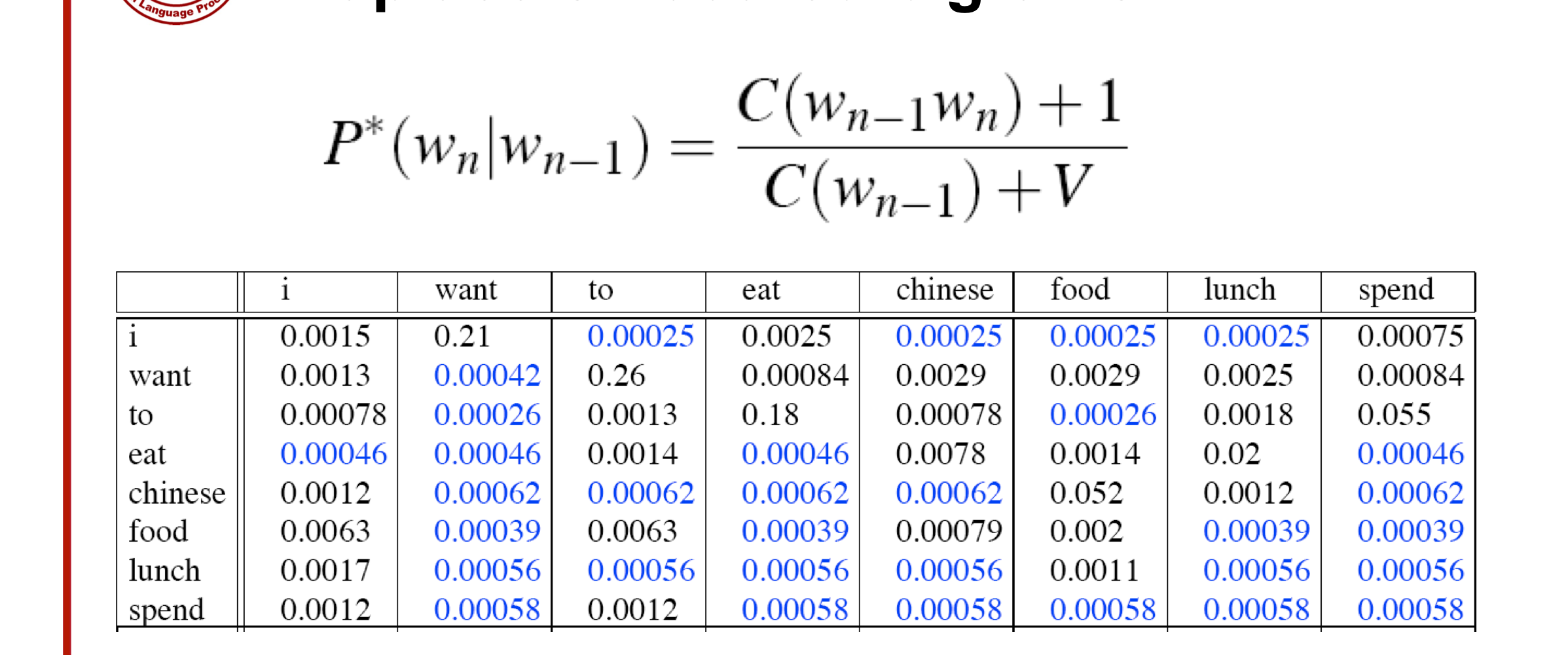
조건부 확률을 기반으로 하기 때문에 같은 1 count라 할지라도 확률은 달라질 수밖에 없습니다.
다만, 이렇게 새롭게 바꾼 확률을 기반으로 다시 카운트를 재구성하면 어떻게 될까요?
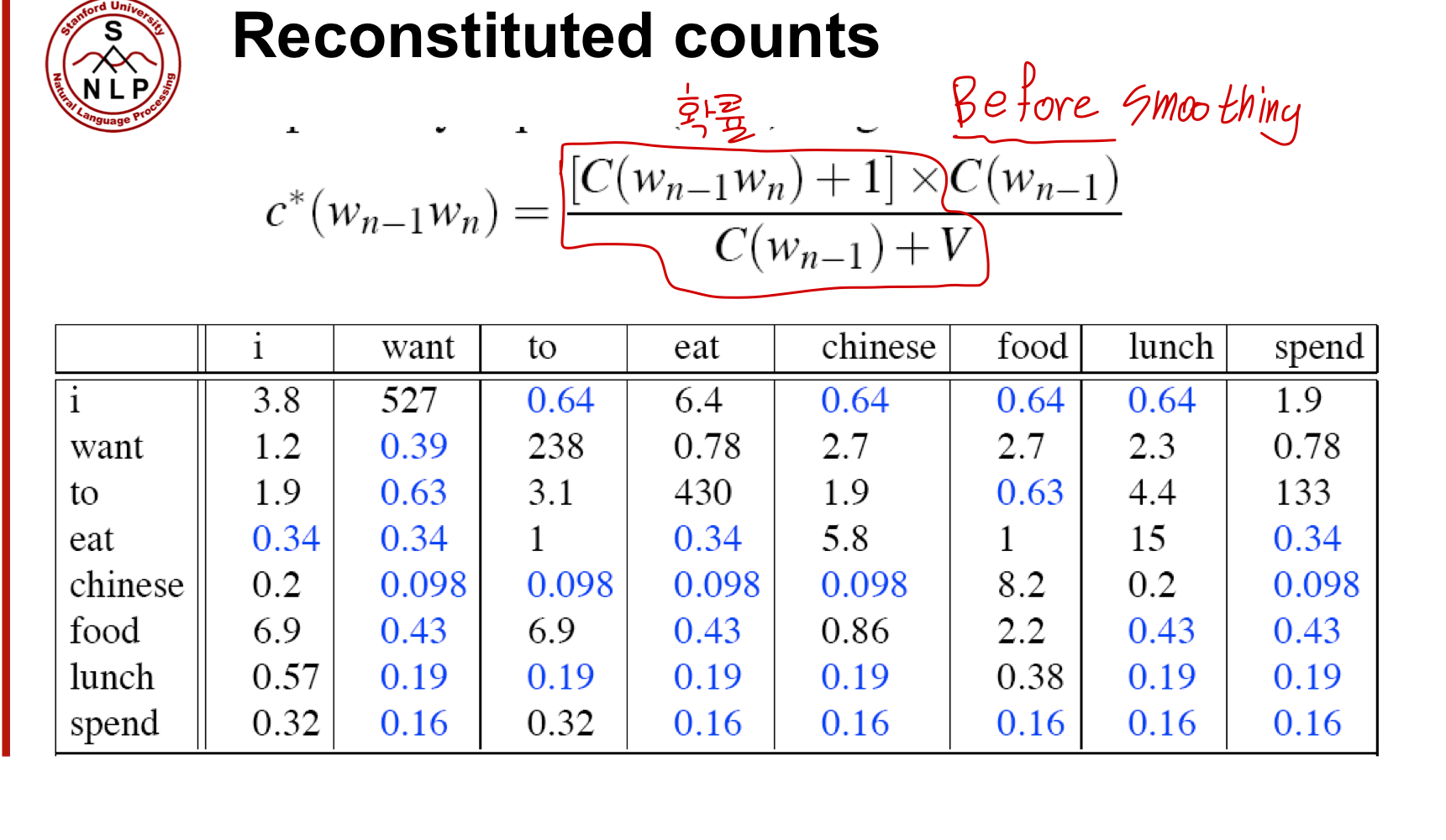
단, 이 때는 smoothing 이전에 나온 unigram count를 곱해줍니다.
그러면, 최종적으로 count가 어떻게 변했을까요.
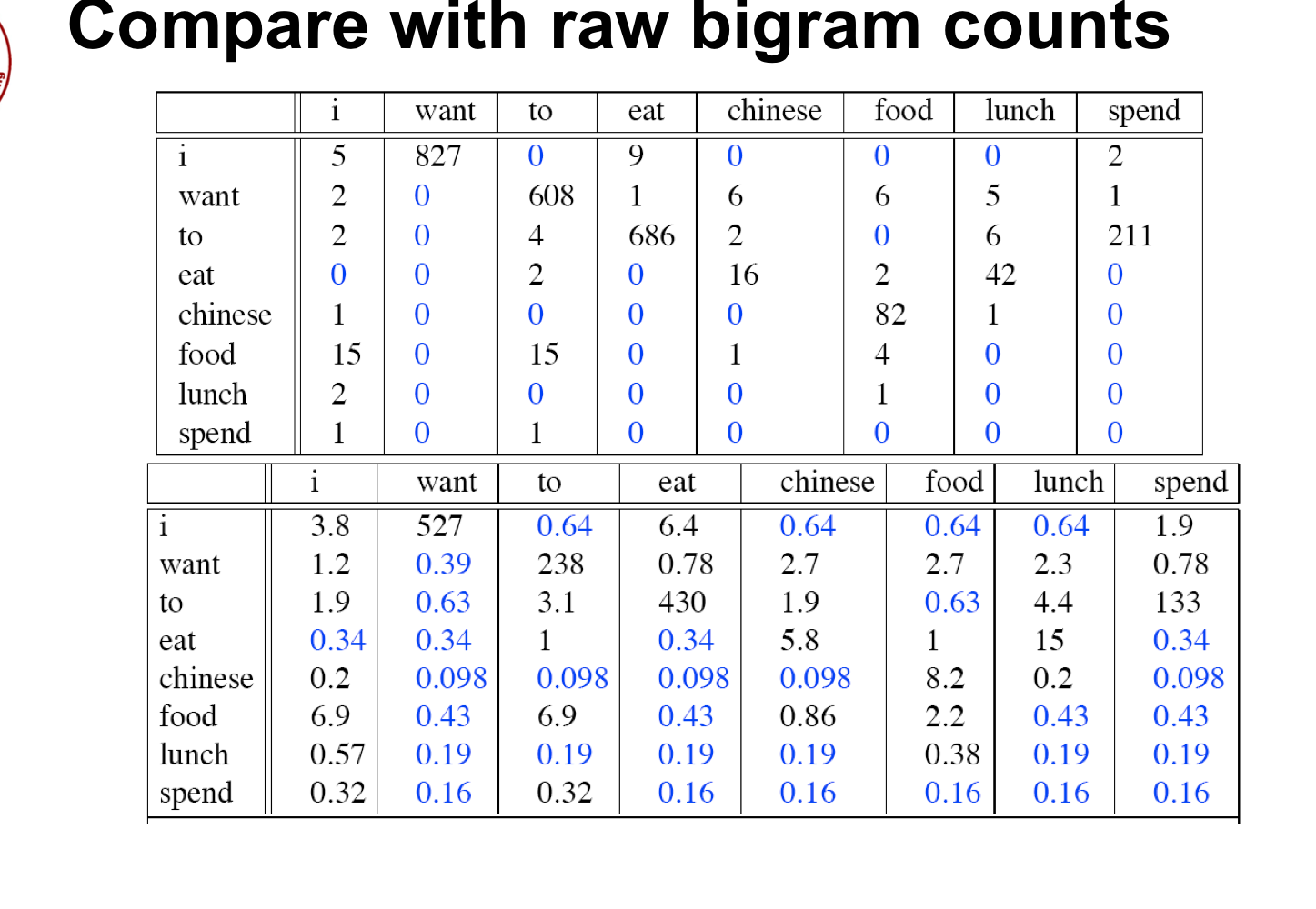
want to : 608 -> 238 (거의 1/3)
chinese food : 82 -> 8.2 (1/10)
- chinese 단어 자체가 want보다는 훨씬 적게 나왔기 때문에.
대신, 파란색으로 나타난 bi-gram 들은 카운팅이 조금 늘어나긴 했습니다.
food - to : 안 나오긴 했지만 0.63
chinese - want : 마찬가지로 안 나오긴 했지만 0.098
이는 단순히 food가 훨씬 많이 나오는 단어이기 때문에, smoothing도 강력하게 들어간 것.
아무튼, count 0을 갖는 요소들에 확률을 부여하기 위해 확률 분포가 누그러졌다는 것에 초점을 두자.
결론적으로,
add-1 smoothings은 text classification이나 다른 nlp기법(0이 많이 나오지 않는 도메인)에 널리 쓰이며, n-gram에는 잘 쓰이지 않는다.
Interpolate
하나의 랭귀지 모델과 또 다른 랭귀지 모델 사이를 잇는 방법을 생각해봅시다.
때로는 context에 너무 의존하지 않는 모델을 사용하고 싶을 때가 있습니다.
즉, 매우 confident한 tri-gram이 있다고 해봅시다.
일반적으로 성능이 좋은.
예를 들어, 어떤 남성의 일기장을 기반으로 학습했을 때,
"나는 여자를 ( )" 라는 tri-gram을 생각해봅시다.
아마, "나는 여자를 좋아한다" 라는 문장이 확률이 높은 trigram이 될 것입니다.
하지만, 모델에게 조금 자유도를 준다든지, 모델이 더 다양한 문장을 생성하게끔 하고싶다든지, 필요성에 따라 위와 같은 trigram을 사용하고 싶지 않을 수도 있습니다.
이럴 때 Backoff, 즉 뒤로 물러나서 조금 더 모델에 불확정성을 주게끔 bi-gram을 대신 사용할 수도 있습니다.
일반적으로는 학습 데이터가 크지 않아 n-gram의 카운트가 낮을 때, 혹은 n-gram에서 n자체가 클 때, 조금 더 작은 모델을 택할 수 있습니다.

또한, 이보다 넓은 개념으로 사용할 수 있는 Interpolation이 있습니다.
즉, 단순히 모델을 단순화하기보다도 여러 모델을 결합해 모델들 사이의 그 어딘가에 있는 새로운 모델을 사용하는 것이죠.
특히, 대부분의 language modeling에서 이러한 interpolation은 효과적이기 때문에, 이를 위주로 다룬다고 합니다.
일반적으로 두 가지 종류의 보간(interpolation)방법이 있습니다.

그러면, lambda는 어떻게 정해질까요?
일반적으로, Held-out corpus를 이용해 정합니다.

validation ㅎㅎ..
즉, Training과 Test 간의 차이를 줄이기 위해, held-out data에 대한 MLE를 수행해 lambad를 정하면 됩니다.
위에서 나타난 (Held-out data에 대한)log-probability를 높히는 방향으로, lambda들을 선정하는 것입니다.
특히, 오른쪽처럼 log-probability의 합으로 결합확률분포를 나타내는 것은 bi-gram일 때만 가능한 건데, 이에 대한 언급이..?
일반적인 과적합 방지 solution과 비슷합니다. 애초에 Generalization을 염두하고 나온게 smoothing, interpolation, ... 이기 때문에.
- 가장 대표적으로는 parameter 학습은 training data로 하되, 성능 평가는 validation data에 진행해 hyper parameter(예를 들어 모델) selection에 사용한다든지..
- 이 둘 간의 exposure bias를 줄이기 위해서 강화학습을 사용하는 방법도 널리 쓰이고 있습니다.
- 또한, Meta-Learning을 이용해서 Test set에서 더 잘 작동하는 area를 찾을 수도 있고,
- 혹은 GPT-3처럼 애초에 Training set의 area를 넓혀 Test set에서 잘 작동하는 area를 감쌀 수도 있습니다.
다시, Zeros count가 있는 상황을 생각해봅시다.
(바로 사용할 수 없기 때문에 다른 카운트로 대체해야합니다)
일반적으로, 우리가 미래에 다루게 될 모든 단어에 대해 알고 있다면 이는 Closed vocabulary task라 합니다.
없겠죠?
그래서 우리는 일반적으로 OOV(Out Of Vocabulary)가 있는 Open vocabulary task를 다룰 때가 많습니다.
이에 대해서 가장 편하게 사용할 수 있는 방법은 special token인 token을 사용하는 것이죠.
한 번도 못 본 단어 뿐만 아니라, 드문 단어도 UNK로 처리하는 게 유리하긴 합니다.
그 후에는 token의 확률을 계산해서 사용하면 됩니다.
사실, 이런 단어가 반환되는 경우는 별로 없지만, 가끔 이러한 rare word나 unknown word를 처리하기 위해 Point net과 같은 개념을 쓰기도 합니다.
Zeros외에도, 또 우리가 다루어야 할 이슈는 Huge web-scale n-grams입니다.
즉, 구글 n-gram corpus처럼 방대한 데이터를 다룰 때에는 corpus에 나타난 모든 n-gram을 고려하기는 쉽지 않습니다.
그래서, prooning 등을 이용해 빈도가 낮은 n-gram은 저장(사용)하지 않는 방법을 취할 수 있습니다.
Test set(즉, held-out set)에서의 Entropy나 복잡도를 기반으로 줄일 수도 있을 것이고,,
또 다른 효율적인 방법들도 사용할 수 있습니다.

아까 add-1 Smoothing은 일반적으로 n-gram task에 잘 안 쓰인다고 했었는데요, **Smoothing을 web-scale n-grams에 적용한다면 어떤 게 제일 많이 쓰일까요?
Stupid backoff는, 이름처럼 아주 간단하지만, 일반적으로 굉장히 잘 작동하는 방법으로 알려져 있습니다.
stupid backoff에 쓰이는 확률은 아래와 같이 계산됩니다.

원래는 0이었던 확률을 다른 확률로 대체하니까 확률의 합은 1보다 커질 것이고, 그래서 를 쓰지는 않습니다.

더 나은 language model을 만들기 위해 task에 맞는 n-gram 모델의 weight를 선택하거나, parsing을 사용하거나, 최근에 쓰이지 않은 단어가 나올 확률이 더 높다는(일반적인 언어의 특성을 반영한) cashing을 사용할 수 있습니다.
cashing 모델은 왜 speech recognition task같은 곳에서 잘 작동하지 않을까요?

Good-Turing Smoothing
위에서 다루었던 Add-1 Smoothing을 일반화해, 새로운 Add-k, UnigramPrior Smoothing 등을 정의해봅시다.
일반적으로, 어떠한 사족도 붙히지 않고 '단어가 등장할 확률'이라는 표현을 한다면, 이는 단어의 사전확률이라고 할 수 있습니다.
특히, Unigram을 뜻하는 경우가 많겠죠. 어떠한 조건도 붙지 않았으니까요.
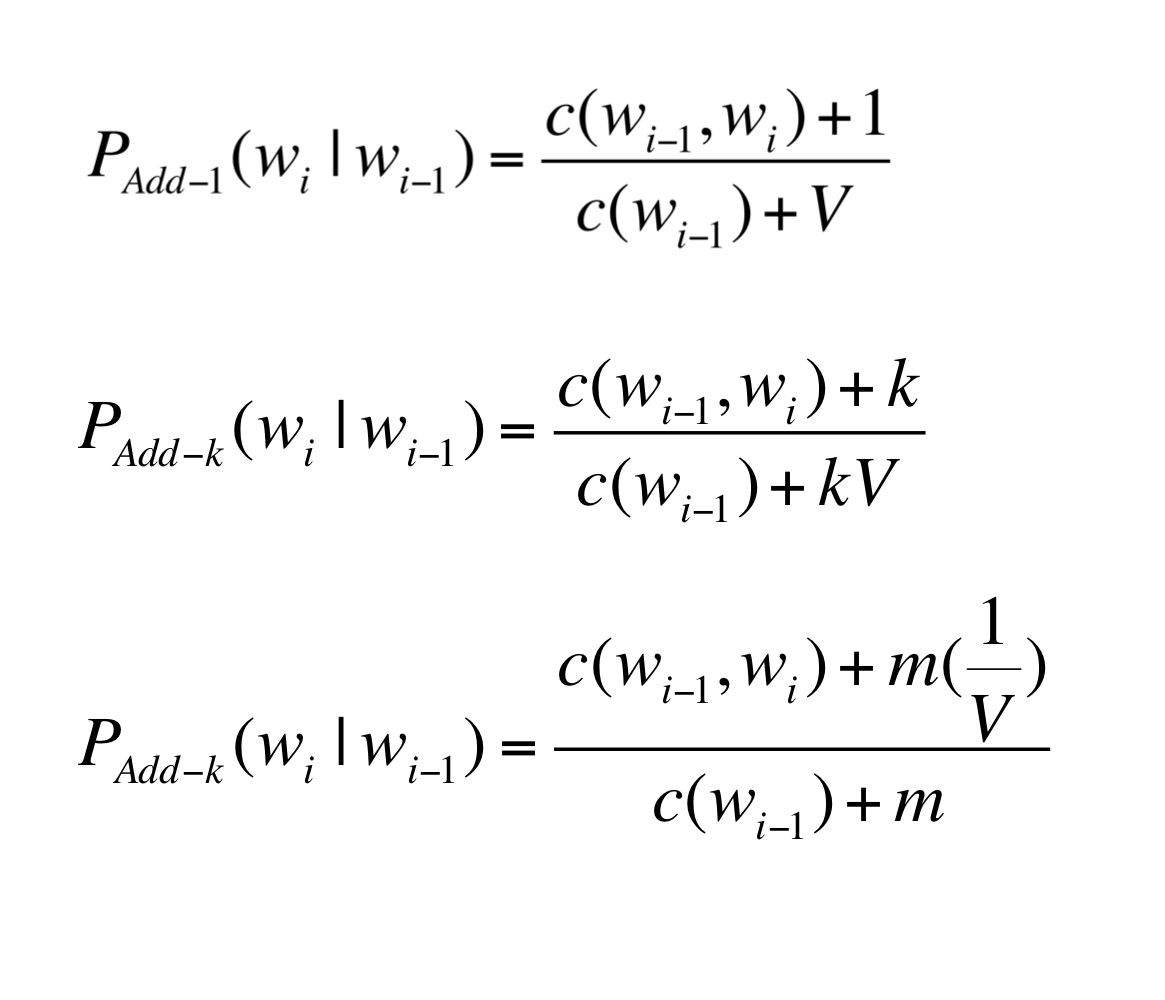
직관적으로 Add-k를 위와 같이 도입하고, 을 활용해 term을 만듭시다. 그러면, 위에서 1/V는 voca 내 모든 단어들에 대한 확률을 동일하게 부여한 확률입니다.
즉, 이처럼 단어들의 확률을 균등분포로 가정하지 않고 단어들의 빈도수를 고려한 확률을 대신 사용할 수 있습니다(Unigram prior).
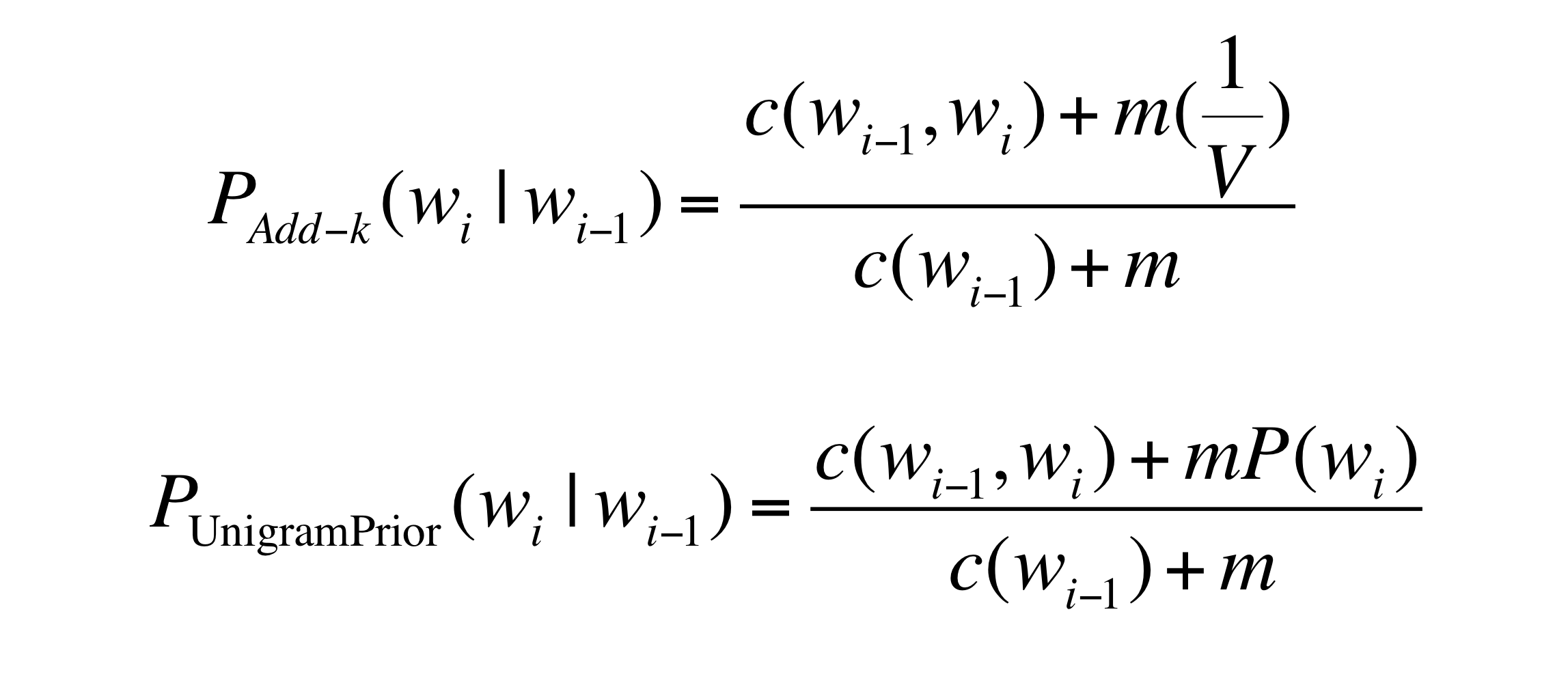
특히, 위처럼 Bi-gram의 확률을 계산하는데 Uni-gram의 확률을 이용했기 때문에 일종의 Interpolation이라고 볼 수도 있습니다.
이런 방법은 잘 작동하긴 합니다만, 그래도 language modeling에는 잘 작동하긴 힘듭니다(애초에 bigram..)
Advanced smoothing algorithms
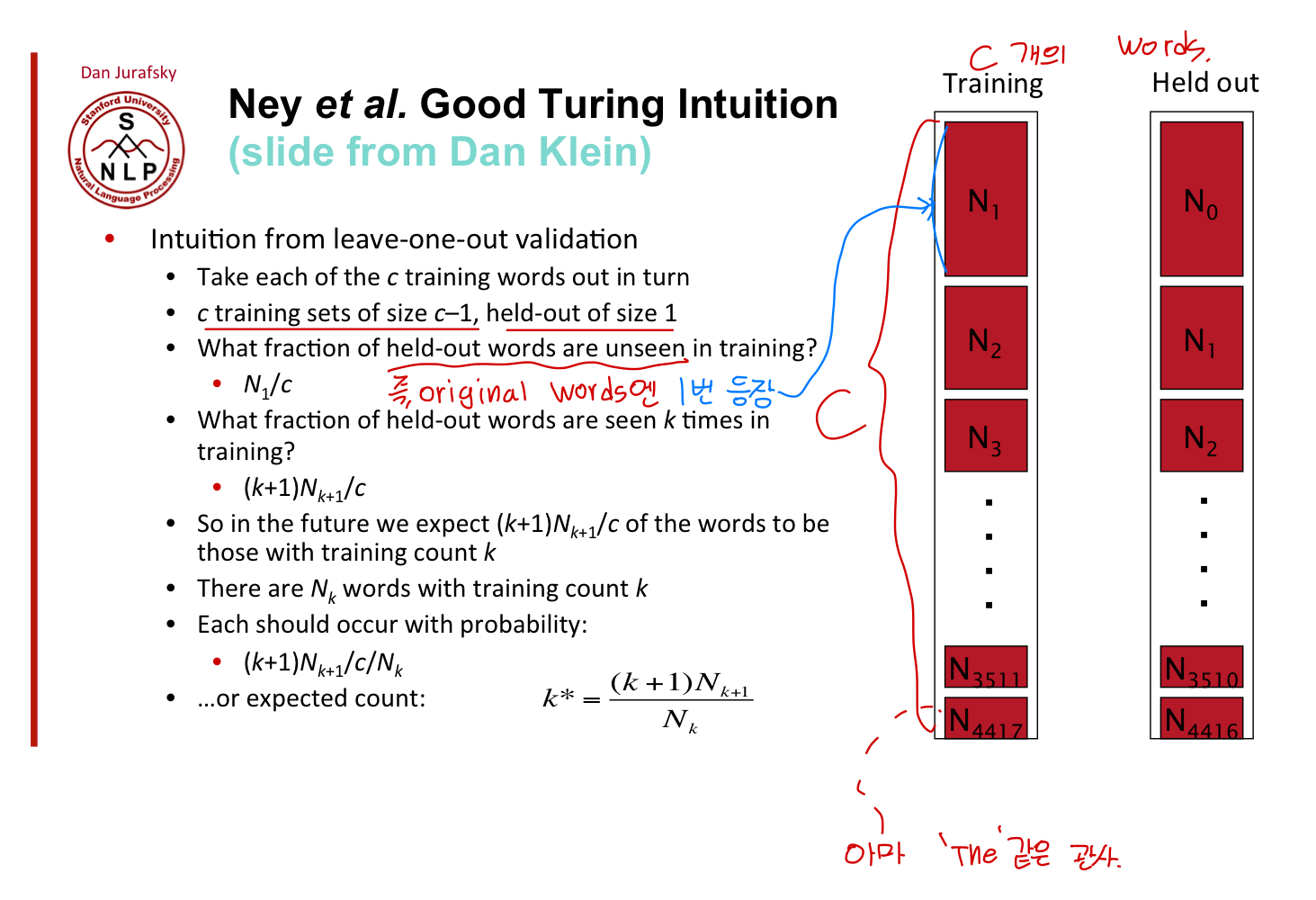
그래서, 아래의 많은 smoothing algorithm들에 쓰인 생각은, "지금까지 보지 못했던 단어들에 대한 counting을 위해서 지금까지 1번 봤던 단어들에 대한 Count를 사용하자"입니다.
- Good-Turing
- Kneser-Ney
- Witten-Bell
즉, Smoothing algorithm들의 목표는 한번도 보지 못한 단어들에 대한 카운트(0)을 대체하는 것이고, 지금까지 한 번만 봤던 단어들은 한번도 보지 못한 단어들과 크게 다를게 없기 때문에, 위와 같은 직관을 사용하는 것입니다.
Notation

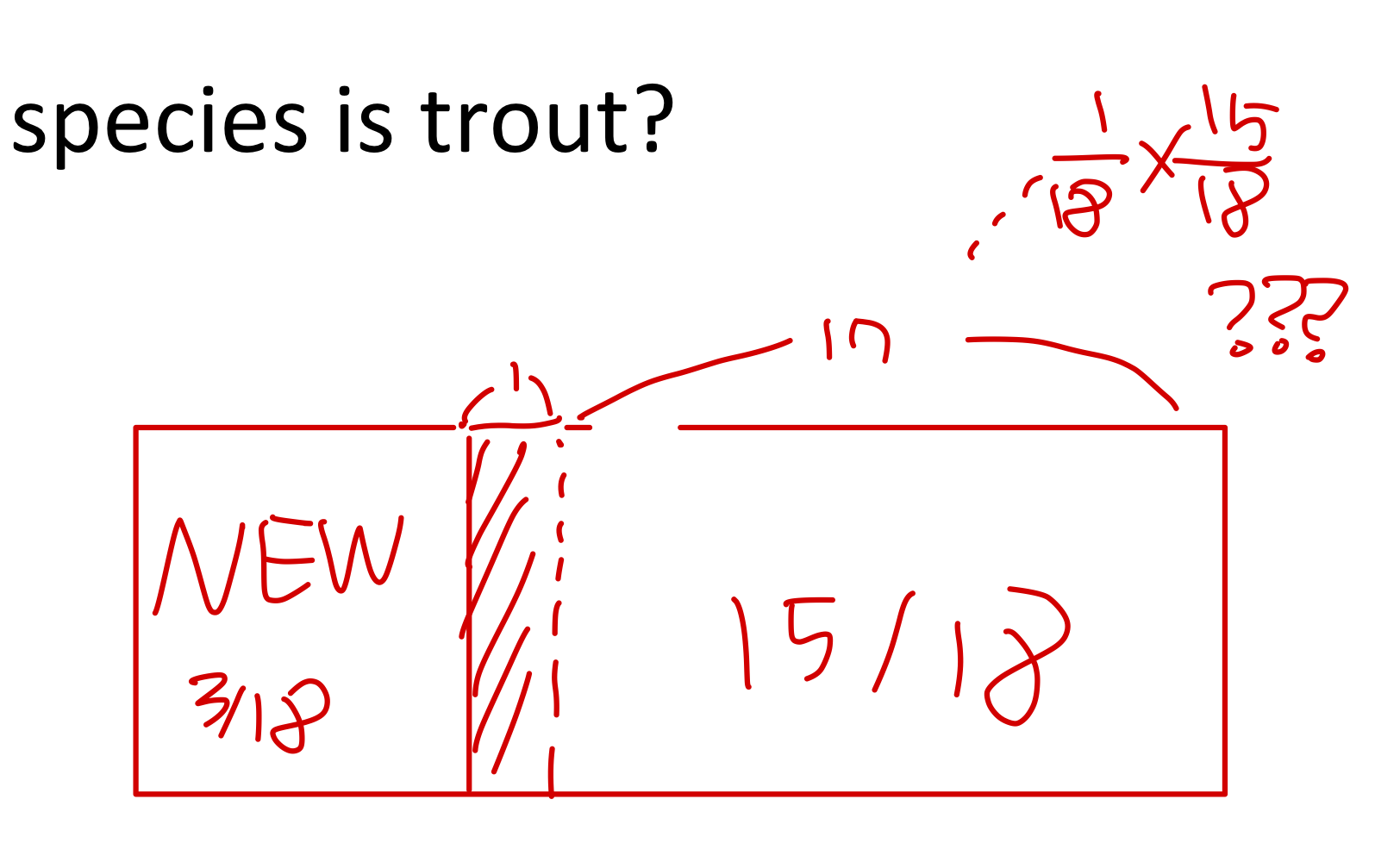
위와 같은 notation, 직관을 Good-Turing Smoothing에 도입해봅시다.

즉, 단순하게 MLE방법을 사용하면 위에서 trout의 확률로 1/18을 예상할 수 있지만, 새로운 종에 대한 확률(추정치) 3/18도 고려를 해주어야 합니다.
그러면, 1/18로 예측했던 추정치는 1/18 미만으로 줄어들겠죠.
그러면 이 줄어드는 확률은 어떤 식으로 반영을 해주어야 될까요.
가장 단순하게는, (확률의 합을 1로 고정하는 방향으로) 기존의 1의 확률에서, 새로운 종에 대한 확률인 3/18만큼 줄어들었으니까, 남은 15/18에 대한 mass만을 고려해, 1/18*15/18로 새로운 확률을 반환할 수 있겠죠.
(이렇게 호락호락하면 좋겠지만, 그리 단순하진 않겠죠. 위에서는 3개의 new-species가 있지만, 여러 가지를 고려했을 때 3개보다 더 높게 반영해야할 수도 있으니까.)
이 부분에 대한 답(equation for Good Turing)은 아래와 같습니다.

(직관적으로) 대강 빈도수가 1인 친구들이 (빈도수 2에 비해)많으면, 새로운 친구들(fish, word)가 나올 확률이 더 높아지는 거니까(분모가 높아지니까), 빈도수가 1인 친구들이 다시 등장할 확률은 낮아지겠죠.
이게 어떤 직관일까..
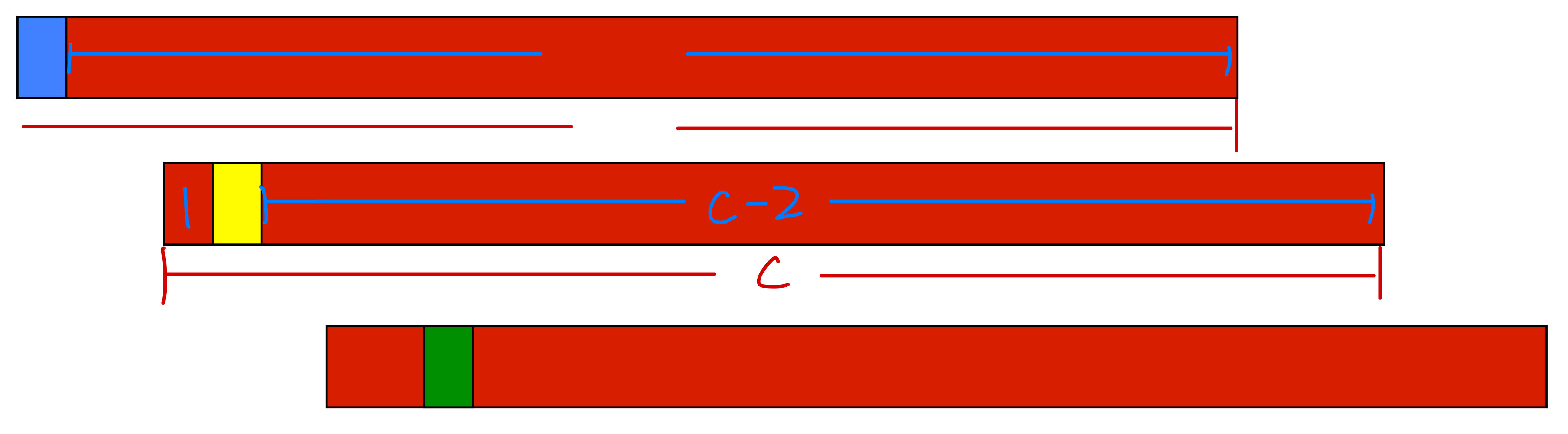
위와 같이 여러 개의 Held-out word를 만들어 봅시다.
(전체 개의 데이터 중 개의 word만 따로 떼어놓는 작업을 여러번..)
즉, 개의 held-out data가 있고, 그 하나하나에 대응하는 개의 길이의 training data가 있습니다.
( 생략 )